Θέματα της 1ης φάσης για την 9η τάξη, 19 Νοεμβρίου 2022
1. Η διαφορά των ριζών του δευτεροβάθμιου τριώνυμου
 είναι
είναι  και η διαφορά των ριζών του τριώνυμου
και η διαφορά των ριζών του τριώνυμου  ,
,  . Με τι μπορεί να ισούται η διαφορά των ριζών του δευτεροβάθμιου τριώνυμου
. Με τι μπορεί να ισούται η διαφορά των ριζών του δευτεροβάθμιου τριώνυμου  ;
; 2. Το καθένα από
 παιδιά κρατάει στα χέρια του ένα πινακάκι με έναν μη μηδενικό αριθμό (θετικό ή αρνητικό), όλοι αυτοί οι αριθμοί είναι διαφορετικοί. Τα παιδιά παρατάχθηκαν κατά φθίνουσα σειρά των αριθμών τους (πρώτα ο μεγαλύτερος αριθμός) και ο Χρήστος προέκυψε να είναι ο τεσσαρακοστός στη σειρά. Ύστερα τα παιδιά παρατάχθηκαν κατά φθίνουσα σειρά, των αντίστροφων των αρχικών αριθμών τους (θυμίζουμε, ότι αντίστροφος ενός αριθμού
παιδιά κρατάει στα χέρια του ένα πινακάκι με έναν μη μηδενικό αριθμό (θετικό ή αρνητικό), όλοι αυτοί οι αριθμοί είναι διαφορετικοί. Τα παιδιά παρατάχθηκαν κατά φθίνουσα σειρά των αριθμών τους (πρώτα ο μεγαλύτερος αριθμός) και ο Χρήστος προέκυψε να είναι ο τεσσαρακοστός στη σειρά. Ύστερα τα παιδιά παρατάχθηκαν κατά φθίνουσα σειρά, των αντίστροφων των αρχικών αριθμών τους (θυμίζουμε, ότι αντίστροφος ενός αριθμού  ονομάζεται ο αριθμός
ονομάζεται ο αριθμός  ) και ο Χρήστος προέκυψε να είναι εξηκοστός. Τέλος, τα παιδιά παρατάχθηκαν κατά φθίνουσα σειρά των τετραγώνων των αρχικών αριθμών τους (όλα τα τετράγωνα προέκυψαν διαφορετικά). Σε ποια θέση κατά σειρά μπορεί να προέκυψε ο Χρήστος; Φέρτε όλες τις δυνατές περιπτώσεις και εξηγήστε γιατί δεν υπάρχουν άλλες.
) και ο Χρήστος προέκυψε να είναι εξηκοστός. Τέλος, τα παιδιά παρατάχθηκαν κατά φθίνουσα σειρά των τετραγώνων των αρχικών αριθμών τους (όλα τα τετράγωνα προέκυψαν διαφορετικά). Σε ποια θέση κατά σειρά μπορεί να προέκυψε ο Χρήστος; Φέρτε όλες τις δυνατές περιπτώσεις και εξηγήστε γιατί δεν υπάρχουν άλλες.3. Το σημείο
 βρίσκεται στην διχοτόμο
βρίσκεται στην διχοτόμο  του τριγώνου
του τριγώνου  . Στην πλευρά
. Στην πλευρά  δίνεται σημείο
δίνεται σημείο  , ώστε
, ώστε 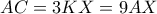 και
και 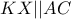 . Αν
. Αν 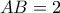 , να βρείτε την περίμετρο του τριγώνου
, να βρείτε την περίμετρο του τριγώνου  .
. 4. Θα ονομάσουμε έναν φυσικό αριθμό (μη μηδενικό) χρήσιμο, αν θα βρεθεί διαιρέτης
 του αριθμού
του αριθμού  τέτοιος, ώστε ο αριθμός
τέτοιος, ώστε ο αριθμός  να είναι τέλειο τετράγωνο. Πόσοι χρήσιμοι αριθμοί υπάρχουν μεταξύ των αριθμών
να είναι τέλειο τετράγωνο. Πόσοι χρήσιμοι αριθμοί υπάρχουν μεταξύ των αριθμών  έως
έως 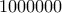 ;
; 5. Ο Βασίλης στα γενέθλιά του έλαβε ως δώρο ένα πίνακα, που αποτελείται από ένα τετράγωνο
 κελιών, στο οποίο έχουν αποκοπεί δυο
κελιών, στο οποίο έχουν αποκοπεί δυο 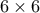 τετράγωνα, αυτό που περιέχει το πάνω αριστερά γωνιακό κελί και αυτό που περιέχει το πάνω δεξιά γωνιακό κελί. Σε κάθε κελί αυτού του πίνακα ο Βασίλης έγραψε έναν φυσικό αριθμό από το
τετράγωνα, αυτό που περιέχει το πάνω αριστερά γωνιακό κελί και αυτό που περιέχει το πάνω δεξιά γωνιακό κελί. Σε κάθε κελί αυτού του πίνακα ο Βασίλης έγραψε έναν φυσικό αριθμό από το  έως το
έως το  , ως αποτέλεσμα κάθε αριθμός συναντάται στον πίνακα περιττό αριθμό φορές. Μια γωνία των τριών κελιών θα την ονομάσουμε πετυχημένη, αν όλοι οι αριθμοί στα κελία της είναι ίσοι μεταξύ τους ή αν είναι όλοι διαφορετικοί. Ο Βασίλης μέτρησε το πλήθος των πετυχημένων γωνιών του πίνακα. Ποιο είναι το ελάχιστο πλήθος που μπορεί να του προέκυψε;
, ως αποτέλεσμα κάθε αριθμός συναντάται στον πίνακα περιττό αριθμό φορές. Μια γωνία των τριών κελιών θα την ονομάσουμε πετυχημένη, αν όλοι οι αριθμοί στα κελία της είναι ίσοι μεταξύ τους ή αν είναι όλοι διαφορετικοί. Ο Βασίλης μέτρησε το πλήθος των πετυχημένων γωνιών του πίνακα. Ποιο είναι το ελάχιστο πλήθος που μπορεί να του προέκυψε;
 ως
ως  τον κάθε ένα περιττό πλήθος φορών. Η μόνο πετυχημένη γωνία είναι αυτή με τους τρείς άσσους.
τον κάθε ένα περιττό πλήθος φορών. Η μόνο πετυχημένη γωνία είναι αυτή με τους τρείς άσσους.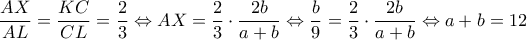

 γράφουμε
γράφουμε  για το πλήθος των αριθμών του κελιού που εμφανίζονται περιττό πλήθος φορών σε αυτό το κελί και
για το πλήθος των αριθμών του κελιού που εμφανίζονται περιττό πλήθος φορών σε αυτό το κελί και  για το πλήθος των πετυχημένων γωνιών. Σε κάθε περίπτωση έχουμε
για το πλήθος των πετυχημένων γωνιών. Σε κάθε περίπτωση έχουμε  . Το άθροισμα όμως όλων των
. Το άθροισμα όμως όλων των  τότε ,
τότε , 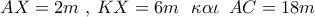 .
.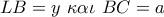 . Από το Θ. Διχοτόμου στο
. Από το Θ. Διχοτόμου στο 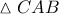 και επειδή
και επειδή 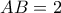 θα έχω ταυτόχρονα:
θα έχω ταυτόχρονα:
 οπότε :
οπότε : 
 οι ρίζες του P είναι
οι ρίζες του P είναι 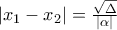 , άρα
, άρα  Όμοια
Όμοια 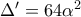 , με
, με 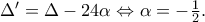
 με
με