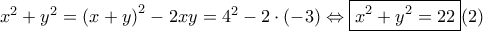Επαρχιακός Διαγωνισμός Λυκείων 2022 (Κύπρος)
Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Επαρχιακός Διαγωνισμός Λυκείων 2022 (Κύπρος)
Σήμερα είχαμε τον Επαρχιακό Διαγωνισμό της Κυπριακής Μαθηματικής Εταιρείας. Αναρτώ εδώ τα θέματα του Λυκείου. Θα αναρτήσω αργότερα και των άλλων τάξεων.
- Συνημμένα
-
- Α' Λυκείου (Ελληνικά).pdf
- (173.02 KiB) Μεταφορτώθηκε 142 φορές
-
- Β' Λυκείου (Ελληνικά).pdf
- (110.86 KiB) Μεταφορτώθηκε 135 φορές
-
- Γ' Λυκείου (Ελληνικά).pdf
- (133.8 KiB) Μεταφορτώθηκε 132 φορές
Λέξεις Κλειδιά:
-
Manolis Petrakis
- Δημοσιεύσεις: 204
- Εγγραφή: Τετ Οκτ 07, 2020 3:19 pm
- Τοποθεσία: Αγρίνιο
Re: Επαρχιακός Διαγωνισμός Λυκείων 2022 (Κύπρος)
Πρόβλημα 1 - Γ' Λυκείου
Είναι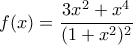
Προφανώς με την ισότητα να ισχύει για
με την ισότητα να ισχύει για  .
.
Για το μέγιστο θα δείξουμε ότι



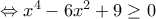
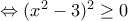
Το οποίο ισχύει, ενώ έχουμε ισότητα για ή
ή  .
.
Για το 2ο ερώτημα, είναι
Επομένως .
.
Πρέπει για κάθε
για κάθε  , άρα και για
, άρα και για  , δηλαδή
, δηλαδή 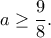
Είναι
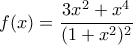
Προφανώς
 με την ισότητα να ισχύει για
με την ισότητα να ισχύει για  .
.Για το μέγιστο θα δείξουμε ότι




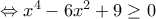
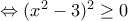
Το οποίο ισχύει, ενώ έχουμε ισότητα για
 ή
ή  .
.Για το 2ο ερώτημα, είναι

Επομένως
 .
.Πρέπει
 για κάθε
για κάθε  , άρα και για
, άρα και για  , δηλαδή
, δηλαδή 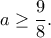
Re: Επαρχιακός Διαγωνισμός Λυκείων 2022 (Κύπρος)
Για το 1ο της Β Λυκείου.
Για έχουμε πως
έχουμε πως 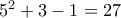 , το οποίο είναι πολλαπλάσιο του 9.
, το οποίο είναι πολλαπλάσιο του 9.
Έστω ότι ισχύει για κάποιο .
.
Τότε για έχουμε :
έχουμε :


Αρκέι να δείξουμε ότι είναι πολλαπλάσιο του
είναι πολλαπλάσιο του  , που ισχύει αφού
, που ισχύει αφού 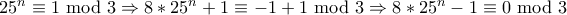
Άρα ισχύει για κάθε θετικό ακέραιο
Για
 έχουμε πως
έχουμε πως 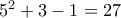 , το οποίο είναι πολλαπλάσιο του 9.
, το οποίο είναι πολλαπλάσιο του 9.Έστω ότι ισχύει για κάποιο
 .
.Τότε για
 έχουμε :
έχουμε :

Αρκέι να δείξουμε ότι
 είναι πολλαπλάσιο του
είναι πολλαπλάσιο του  , που ισχύει αφού
, που ισχύει αφού 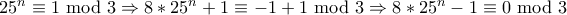
Άρα ισχύει για κάθε θετικό ακέραιο

-
CarlusMagnsenYourDad22
- Δημοσιεύσεις: 8
- Εγγραφή: Τρί Οκτ 18, 2022 9:03 pm
Re: Επαρχιακός Διαγωνισμός Λυκείων 2022 (Κύπρος)
Π1 Β ΛΥΚΕΙΟΥ:
Παρατηρούμε(mod 9):
n, 5^2n, 3n, -1
1, 7, 3, -1
2, 4, 6, -1
3, 1, 0, -1
4, 7, 3, -1
...
Άρα σε κάθε περίπτωση 5^2n+3n-1=0 (mod 9)και το ζητούμενο έπεται.
Παρατηρούμε(mod 9):
n, 5^2n, 3n, -1
1, 7, 3, -1
2, 4, 6, -1
3, 1, 0, -1
4, 7, 3, -1
...
Άρα σε κάθε περίπτωση 5^2n+3n-1=0 (mod 9)και το ζητούμενο έπεται.
Re: Επαρχιακός Διαγωνισμός Λυκείων 2022 (Κύπρος)
Για το 4ο της Γ λυκείου
Αρκεί να αποδείξουμε ότι .
.
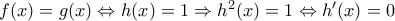
Αφού τότε
τότε 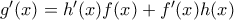
Άρα για κάθε αριθμό ώστε
ώστε  , ισχύει επίσης ότι
, ισχύει επίσης ότι  .
.
Οπότε , και το ζητούμενο έπεται.
, και το ζητούμενο έπεται.
Αρκεί να αποδείξουμε ότι
 .
. 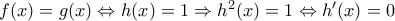
Αφού
 τότε
τότε 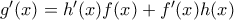
Άρα για κάθε αριθμό
 ώστε
ώστε  , ισχύει επίσης ότι
, ισχύει επίσης ότι  .
. Οπότε
 , και το ζητούμενο έπεται.
, και το ζητούμενο έπεται.-
CarlusMagnsenYourDad22
- Δημοσιεύσεις: 8
- Εγγραφή: Τρί Οκτ 18, 2022 9:03 pm
Re: Επαρχιακός Διαγωνισμός Λυκείων 2022 (Κύπρος)
Π4 Β ΛΥΚΕΙΟΥ:
Φέρνω ΒΔ=ΒΑ=γ στην προέκταση της ΓΒ.
ΑΒΓ όμοιο με ΑΔΓ από Γ-Γ. Άρα β/α=(α+γ)/β και το ζητούμενο έπεται.
Φέρνω ΒΔ=ΒΑ=γ στην προέκταση της ΓΒ.
ΑΒΓ όμοιο με ΑΔΓ από Γ-Γ. Άρα β/α=(α+γ)/β και το ζητούμενο έπεται.
- Συνημμένα
-
- Screenshot_20221113_101910.png (55.92 KiB) Προβλήθηκε 1036 φορές
-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5561
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
Re: Επαρχιακός Διαγωνισμός Λυκείων 2022 (Κύπρος)
Χαίρομαι που στη Γεωμετρια της Β Λυκειου τέθηκε κλιμακωτά το θεώρημα της σπασμένης χορδής του Αρχιμήδη κάτι που νομίζω ότι αξίζει να αναφερθεί στις λύσεις, έτσι για την ιστορία κλπ.
Καλά αποτελέσματα !
Καλά αποτελέσματα !
- S.E.Louridas
- Δημοσιεύσεις: 5956
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
Re: Επαρχιακός Διαγωνισμός Λυκείων 2022 (Κύπρος)
Και μία άλλη λύση για το 1ο πρόβλημα της Β' Λυκείου, εκτός εκείνης με την τέλεια επαγωγή, για να δούμε και τη δύναμη του διωνύμου.
 οπότε αρκεί
οπότε αρκεί  ή αρκεί
ή αρκεί  οπότε αρκεί
οπότε αρκεί  άρα αρκεί
άρα αρκεί  που είναι καθαρό ότι ισχύει.
που είναι καθαρό ότι ισχύει.
 οπότε αρκεί
οπότε αρκεί  ή αρκεί
ή αρκεί  οπότε αρκεί
οπότε αρκεί  άρα αρκεί
άρα αρκεί  που είναι καθαρό ότι ισχύει.
που είναι καθαρό ότι ισχύει.S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
- S.E.Louridas
- Δημοσιεύσεις: 5956
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
Re: Επαρχιακός Διαγωνισμός Λυκείων 2022 (Κύπρος)
Για το 4ο πρόβλημα της Β’ Λυκείου:
Θεωρούμε την διχοτόμο Θέλουμε να ισχύει
Θέλουμε να ισχύει 
Έχουμε
Όμως άρα
άρα 
Θεωρούμε την διχοτόμο
 Θέλουμε να ισχύει
Θέλουμε να ισχύει 
Έχουμε

Όμως
 άρα
άρα 
S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
-
Henri van Aubel
- Δημοσιεύσεις: 876
- Εγγραφή: Τρί Σεπ 13, 2022 12:01 pm
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες