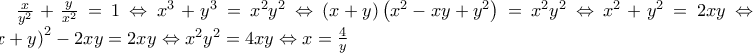Καλημέρα! Δεν υπάρχουν και οι περιπτώσεις που το Δ βρίσκεται π.χ. Στο ημιεπίπεδο που ορίζει το ΑΒ και δεν ανήκει το Γ;george visvikis έγραψε: ↑Σάβ Νοέμ 12, 2022 9:54 amB Λυκείου Π.3
Για τον εντοπισμό τουΒ.Π.3.png
Κατασκευάζω το τόξο χορδήςπου δέχεται γωνία
και τόξο χορδής
που δέχεται γωνία
Τα δύο αυτά τόξα έχουν ήδη ένα κοινό σημείο το
άρα θα έχουν και δεύτερο μοναδικό κοινό σημείο, έστω
ΘΑΛΗΣ 2022
Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
-
CarlusMagnsenYourDad22
- Δημοσιεύσεις: 8
- Εγγραφή: Τρί Οκτ 18, 2022 9:03 pm
Re: ΘΑΛΗΣ 2022
Λέξεις Κλειδιά:
- matha
- Γενικός Συντονιστής
- Δημοσιεύσεις: 6423
- Εγγραφή: Παρ Μάιος 21, 2010 7:40 pm
- Τοποθεσία: Θεσσαλονίκη
Re: ΘΑΛΗΣ 2022
Θέμα 1ο Γ' Λυκείου:
Μια ακόμα αντιμετώπιση με μια ιδέα που έχουμε ξανασυζητήσει.
Θέτουμε![\displaystyle{a=1+x,b=1-x, x\in [-1,1].} \displaystyle{a=1+x,b=1-x, x\in [-1,1].}](/forum/ext/geomar/texintegr/latexrender/pictures/1bdae221872f5265ea0fb7fadce408a6.png)
Είναι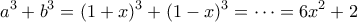 και
και 
Επομένως δηλαδή
δηλαδή 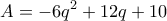 όπου
όπου ![\displaystyle{q\in [0,1].} \displaystyle{q\in [0,1].}](/forum/ext/geomar/texintegr/latexrender/pictures/f17cf37d85aefc1f556599d56ef66b56.png)
Τώρα φανερά , οπότε
, οπότε  με την ισότητα π.χ. για
με την ισότητα π.χ. για 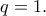
Επίσης αφού
αφού 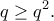 Επομένως
Επομένως  με την ισότητα για
με την ισότητα για 
Μια ακόμα αντιμετώπιση με μια ιδέα που έχουμε ξανασυζητήσει.
Θέτουμε
![\displaystyle{a=1+x,b=1-x, x\in [-1,1].} \displaystyle{a=1+x,b=1-x, x\in [-1,1].}](/forum/ext/geomar/texintegr/latexrender/pictures/1bdae221872f5265ea0fb7fadce408a6.png)
Είναι
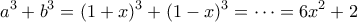 και
και 
Επομένως
 δηλαδή
δηλαδή 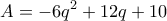 όπου
όπου ![\displaystyle{q\in [0,1].} \displaystyle{q\in [0,1].}](/forum/ext/geomar/texintegr/latexrender/pictures/f17cf37d85aefc1f556599d56ef66b56.png)
Τώρα φανερά
 , οπότε
, οπότε  με την ισότητα π.χ. για
με την ισότητα π.χ. για 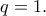
Επίσης
 αφού
αφού 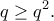 Επομένως
Επομένως  με την ισότητα για
με την ισότητα για 
Μάγκος Θάνος
-
Nick Rapanos
- Δημοσιεύσεις: 50
- Εγγραφή: Τρί Απρ 07, 2009 2:18 am
Re: ΘΑΛΗΣ 2022
Πρόβλημα 3 - B' Γυμνασίου
1η Προσέγγιση
Έστω ότι ο κύριος Γιάννης δίνει καραμέλες στον Δημήτρη,
καραμέλες στον Δημήτρη,  στον Γιώργο και συνεπώς μένουν
στον Γιώργο και συνεπώς μένουν  καραμέλες στη σακούλα.
καραμέλες στη σακούλα.
Παρατηρούμε ότι προκειμένου να αντιστραφούν οι ρόλοι και να έχει ο Δημήτρης επτά φορές περισσότερες καραμέλες από τον Γιώργο θα πρέπει ο Γιώργος να φάει "πολλές" καραμέλες χωρίς να συμπληρώσει παράλληλα από τη σακούλα, ενώ ο Δημήτρης θα πρέπει να κάνει το αντίθετο, δηλαδή να φάει "λίγες" καραμέλες και να συμπληρώσει όσο το δυνατόν περισσότερες από τη σακούλα.
Πιο συγκεκριμένα, τα παιδιά θα φάνε τον ελάχιστο αριθμό καραμελών όταν ο Δημήτρης δε φάει καμία καραμέλα και συμπληρώσει το μέγιστο δυνατό αριθμό καραμελών από τη σακούλα (δλδ ), ενώ ο Γιώργος θα πρέπει να φάει αρκετές ώστε να μείνει με το ένα έβδομο του αριθμού των καραμελών του Γιώργου.
), ενώ ο Γιώργος θα πρέπει να φάει αρκετές ώστε να μείνει με το ένα έβδομο του αριθμού των καραμελών του Γιώργου.
Καταρχάς να εξηγήσουμε ότι ο Δημήτρης δεν μπορεί να πάρει καραμέλες από τη σακούλα γιατί τότε θα έμεναν μηδέν καραμέλες στη σακούλα και θα έπρεπε όλοι να έχουν μηδέν στην κατοχή τους στο τέλος. Μπορεί όμως ο Δημήτρης να μη φάει καμία καραμέλα και να πάρει
καραμέλες από τη σακούλα γιατί τότε θα έμεναν μηδέν καραμέλες στη σακούλα και θα έπρεπε όλοι να έχουν μηδέν στην κατοχή τους στο τέλος. Μπορεί όμως ο Δημήτρης να μη φάει καμία καραμέλα και να πάρει  καραμέλες από τη σακούλα, οπότε καταλήγει με
καραμέλες από τη σακούλα, οπότε καταλήγει με 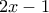 καραμέλες ο Δημήτρης και 1 στη σακούλα. Αλλά γνωρίζουμε ότι
καραμέλες ο Δημήτρης και 1 στη σακούλα. Αλλά γνωρίζουμε ότι  , επομένως
, επομένως  . Εύκολα δείχνει κανείς ότι σε αυτή την περίπτωση ξεκινήσαμε με 36 καραμέλες και ο Γιώργος πρέπει να φάει τουλάχιστον 27 καραμέλες, δηλαδή τουλάχιστον τα
. Εύκολα δείχνει κανείς ότι σε αυτή την περίπτωση ξεκινήσαμε με 36 καραμέλες και ο Γιώργος πρέπει να φάει τουλάχιστον 27 καραμέλες, δηλαδή τουλάχιστον τα 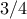 της σακούλας. Σε οποιαδήποτε άλλη περίπτωση, ο Δημήτρης είτε τρώει κι αυτός κάποιες καραμέλες είτε παίρνει λιγότερες από τη σακούλα - πράγμα που σημαίνει ότι ο Γιώργος πρέπει να φάει ακόμη περισσότερες καραμέλες για να μείνει με το ένα έβδομο των καραμελών του Δημήτρη. 'Αρα πράγματι, τα παιδιά έφαγαν τουλάχιστον τα
της σακούλας. Σε οποιαδήποτε άλλη περίπτωση, ο Δημήτρης είτε τρώει κι αυτός κάποιες καραμέλες είτε παίρνει λιγότερες από τη σακούλα - πράγμα που σημαίνει ότι ο Γιώργος πρέπει να φάει ακόμη περισσότερες καραμέλες για να μείνει με το ένα έβδομο των καραμελών του Δημήτρη. 'Αρα πράγματι, τα παιδιά έφαγαν τουλάχιστον τα 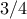 από τις συνολικές καραμέλες που αγόρασε ο κύριος Γιάννης.
από τις συνολικές καραμέλες που αγόρασε ο κύριος Γιάννης.
2η Προσέγγιση
Έστω ότι τα παιδιά έφαγαν καραμέλες και έχουν μέινει με
καραμέλες και έχουν μέινει με  o Δημήτρης,
o Δημήτρης,  ο Γιώργος, και
ο Γιώργος, και  στη σακούλα.
στη σακούλα.
Τότε .
.
Η άσκηση μας ζητάει να αποδείξουμε ότι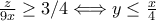 .
.
Αρχικά, το άθροισμα των καραμελών του Δημήτρη και της σακούλας είναι . Αφού ο Δημήτρης φάει κάποιες καραμέλες και πάρει και κάποιες από τη σακούλα (ενώ παράλληλα μπορεί και ο Γιώργος να πάρει καραμέλες από τη σακούλα), μένουν
. Αφού ο Δημήτρης φάει κάποιες καραμέλες και πάρει και κάποιες από τη σακούλα (ενώ παράλληλα μπορεί και ο Γιώργος να πάρει καραμέλες από τη σακούλα), μένουν  στον Δημήτρη και
στον Δημήτρη και  στη σακούλα, δηλαδή
στη σακούλα, δηλαδή  συνολικά. Το άθροισμα όμως των καραμελών του Δημήτρη και της σακούλας δεν μπορεί να είναι μεγαλύτερο από το αρχικό, άρα
συνολικά. Το άθροισμα όμως των καραμελών του Δημήτρη και της σακούλας δεν μπορεί να είναι μεγαλύτερο από το αρχικό, άρα

και η απόδειξη ολοκληρώθηκε.
Σημείωση. Σε τέτοιου είδους προβλήματα που φαίνεται να έχουμε περισσότερους <<αγνώστους>> από εξισώσεις, σκέφτομαι τρία πράγματα:
1. Το πρόβλημα δε μου ζητάει να βρώ όλους τους <<αγνώστους>> αλλά να αποδείξω κάποια σχέση για αυτούς. Αυτό μπορεί να είναι εφικτό ακόμη κι αν δεν μπορώ να λύσω για τους αγνώστους.
2. Συνήθως ψάχνω να βρώ αναλλοίωτες ποσότητες που θα χρησιμέυσουν στη λύση του προβλήματος. Εδώ η αναλλοίωτη ποσότητα ήταν οι συνολικές καραμέλες (μετρώντας της καραμέλες του Γιώργου, του Δημήτρη, της σακούλας, καθώς και αυτές που έφαγαν τα παιδιά).
3. Ακόμη και όταν δεν μπορώ να λύσω το πρόβλημα φορμαλιστικά (βλ. 2η Προσέγγιση), προσπαθώ με απλές σκέψεις και παραδείγματα να προσδιορίσω τις ακραίες περιπτώσεις του προβλήματος και αυτό ισώς με βοηθήσει στη λύση του (βλ. 1η Προσέγγιση).
Καλή επιτυχία και καλή διασκέδαση!
Ν
1η Προσέγγιση
Έστω ότι ο κύριος Γιάννης δίνει
 καραμέλες στον Δημήτρη,
καραμέλες στον Δημήτρη,  στον Γιώργο και συνεπώς μένουν
στον Γιώργο και συνεπώς μένουν  καραμέλες στη σακούλα.
καραμέλες στη σακούλα.Παρατηρούμε ότι προκειμένου να αντιστραφούν οι ρόλοι και να έχει ο Δημήτρης επτά φορές περισσότερες καραμέλες από τον Γιώργο θα πρέπει ο Γιώργος να φάει "πολλές" καραμέλες χωρίς να συμπληρώσει παράλληλα από τη σακούλα, ενώ ο Δημήτρης θα πρέπει να κάνει το αντίθετο, δηλαδή να φάει "λίγες" καραμέλες και να συμπληρώσει όσο το δυνατόν περισσότερες από τη σακούλα.
Πιο συγκεκριμένα, τα παιδιά θα φάνε τον ελάχιστο αριθμό καραμελών όταν ο Δημήτρης δε φάει καμία καραμέλα και συμπληρώσει το μέγιστο δυνατό αριθμό καραμελών από τη σακούλα (δλδ
 ), ενώ ο Γιώργος θα πρέπει να φάει αρκετές ώστε να μείνει με το ένα έβδομο του αριθμού των καραμελών του Γιώργου.
), ενώ ο Γιώργος θα πρέπει να φάει αρκετές ώστε να μείνει με το ένα έβδομο του αριθμού των καραμελών του Γιώργου. Καταρχάς να εξηγήσουμε ότι ο Δημήτρης δεν μπορεί να πάρει
 καραμέλες από τη σακούλα γιατί τότε θα έμεναν μηδέν καραμέλες στη σακούλα και θα έπρεπε όλοι να έχουν μηδέν στην κατοχή τους στο τέλος. Μπορεί όμως ο Δημήτρης να μη φάει καμία καραμέλα και να πάρει
καραμέλες από τη σακούλα γιατί τότε θα έμεναν μηδέν καραμέλες στη σακούλα και θα έπρεπε όλοι να έχουν μηδέν στην κατοχή τους στο τέλος. Μπορεί όμως ο Δημήτρης να μη φάει καμία καραμέλα και να πάρει  καραμέλες από τη σακούλα, οπότε καταλήγει με
καραμέλες από τη σακούλα, οπότε καταλήγει με 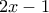 καραμέλες ο Δημήτρης και 1 στη σακούλα. Αλλά γνωρίζουμε ότι
καραμέλες ο Δημήτρης και 1 στη σακούλα. Αλλά γνωρίζουμε ότι  , επομένως
, επομένως  . Εύκολα δείχνει κανείς ότι σε αυτή την περίπτωση ξεκινήσαμε με 36 καραμέλες και ο Γιώργος πρέπει να φάει τουλάχιστον 27 καραμέλες, δηλαδή τουλάχιστον τα
. Εύκολα δείχνει κανείς ότι σε αυτή την περίπτωση ξεκινήσαμε με 36 καραμέλες και ο Γιώργος πρέπει να φάει τουλάχιστον 27 καραμέλες, δηλαδή τουλάχιστον τα 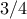 της σακούλας. Σε οποιαδήποτε άλλη περίπτωση, ο Δημήτρης είτε τρώει κι αυτός κάποιες καραμέλες είτε παίρνει λιγότερες από τη σακούλα - πράγμα που σημαίνει ότι ο Γιώργος πρέπει να φάει ακόμη περισσότερες καραμέλες για να μείνει με το ένα έβδομο των καραμελών του Δημήτρη. 'Αρα πράγματι, τα παιδιά έφαγαν τουλάχιστον τα
της σακούλας. Σε οποιαδήποτε άλλη περίπτωση, ο Δημήτρης είτε τρώει κι αυτός κάποιες καραμέλες είτε παίρνει λιγότερες από τη σακούλα - πράγμα που σημαίνει ότι ο Γιώργος πρέπει να φάει ακόμη περισσότερες καραμέλες για να μείνει με το ένα έβδομο των καραμελών του Δημήτρη. 'Αρα πράγματι, τα παιδιά έφαγαν τουλάχιστον τα 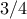 από τις συνολικές καραμέλες που αγόρασε ο κύριος Γιάννης.
από τις συνολικές καραμέλες που αγόρασε ο κύριος Γιάννης.2η Προσέγγιση
Έστω ότι τα παιδιά έφαγαν
 καραμέλες και έχουν μέινει με
καραμέλες και έχουν μέινει με  o Δημήτρης,
o Δημήτρης,  ο Γιώργος, και
ο Γιώργος, και  στη σακούλα.
στη σακούλα. Τότε
 .
.Η άσκηση μας ζητάει να αποδείξουμε ότι
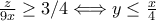 .
.Αρχικά, το άθροισμα των καραμελών του Δημήτρη και της σακούλας είναι
 . Αφού ο Δημήτρης φάει κάποιες καραμέλες και πάρει και κάποιες από τη σακούλα (ενώ παράλληλα μπορεί και ο Γιώργος να πάρει καραμέλες από τη σακούλα), μένουν
. Αφού ο Δημήτρης φάει κάποιες καραμέλες και πάρει και κάποιες από τη σακούλα (ενώ παράλληλα μπορεί και ο Γιώργος να πάρει καραμέλες από τη σακούλα), μένουν  στον Δημήτρη και
στον Δημήτρη και  στη σακούλα, δηλαδή
στη σακούλα, δηλαδή  συνολικά. Το άθροισμα όμως των καραμελών του Δημήτρη και της σακούλας δεν μπορεί να είναι μεγαλύτερο από το αρχικό, άρα
συνολικά. Το άθροισμα όμως των καραμελών του Δημήτρη και της σακούλας δεν μπορεί να είναι μεγαλύτερο από το αρχικό, άρα
και η απόδειξη ολοκληρώθηκε.
Σημείωση. Σε τέτοιου είδους προβλήματα που φαίνεται να έχουμε περισσότερους <<αγνώστους>> από εξισώσεις, σκέφτομαι τρία πράγματα:
1. Το πρόβλημα δε μου ζητάει να βρώ όλους τους <<αγνώστους>> αλλά να αποδείξω κάποια σχέση για αυτούς. Αυτό μπορεί να είναι εφικτό ακόμη κι αν δεν μπορώ να λύσω για τους αγνώστους.
2. Συνήθως ψάχνω να βρώ αναλλοίωτες ποσότητες που θα χρησιμέυσουν στη λύση του προβλήματος. Εδώ η αναλλοίωτη ποσότητα ήταν οι συνολικές καραμέλες (μετρώντας της καραμέλες του Γιώργου, του Δημήτρη, της σακούλας, καθώς και αυτές που έφαγαν τα παιδιά).
3. Ακόμη και όταν δεν μπορώ να λύσω το πρόβλημα φορμαλιστικά (βλ. 2η Προσέγγιση), προσπαθώ με απλές σκέψεις και παραδείγματα να προσδιορίσω τις ακραίες περιπτώσεις του προβλήματος και αυτό ισώς με βοηθήσει στη λύση του (βλ. 1η Προσέγγιση).
Καλή επιτυχία και καλή διασκέδαση!
Ν
τελευταία επεξεργασία από Nick Rapanos σε Σάβ Νοέμ 12, 2022 12:04 pm, έχει επεξεργασθεί 1 φορά συνολικά.
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13278
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: ΘΑΛΗΣ 2022
Όχι δεν μπορεί να συμβεί αυτό, γιατί τότε θα είναιCarlusMagnsenYourDad22 έγραψε: ↑Σάβ Νοέμ 12, 2022 11:17 amΚαλημέρα! Δεν υπάρχουν και οι περιπτώσεις που το Δ βρίσκεται π.χ. Στο ημιεπίπεδο που ορίζει το ΑΒ και δεν ανήκει το Γ;george visvikis έγραψε: ↑Σάβ Νοέμ 12, 2022 9:54 amB Λυκείου Π.3
Για τον εντοπισμό τουΒ.Π.3.png
Κατασκευάζω το τόξο χορδήςπου δέχεται γωνία
και τόξο χορδής
που δέχεται γωνία
Τα δύο αυτά τόξα έχουν ήδη ένα κοινό σημείο το
άρα θα έχουν και δεύτερο μοναδικό κοινό σημείο, έστω
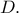
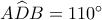 και όχι
και όχι 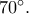
Re: ΘΑΛΗΣ 2022
Εγώ ως μαθητής της Β λυκείου μου πήρε περίπου 1-1.30 ώρα στον διαγωνισμό να λύσω τα πρώτα 2 θέματα...(Βέβαια το 2ο με έναν αρκτα περίεργο τροπο) , ενώ το 1ο και το 3ο πρόβλημα της 3ης Λυκείου τα βρήκα αρκετά εύκολα(Μου πήραν περίπου 10 λεπτά συνολικά)....
Re: ΘΑΛΗΣ 2022
Χμμ...θα μπορούσα να σχολιάσω πολλά, αλλά θα αρκεστώ στις εξής παρατηρήσεις:
1. Οι βάσεις καθορίζονται ανά τάξη μετά τη βαθμολόγηση όλων των γραπτών.
2. Καλά αποτελέσματα και καλή επιτυχία στον ΑΡΧΙΜΗΔΗ των μεγάλων, όπου τα θέματα θα είναι κοινά για όλες τις τάξεις του Λυκείου.
Φιλικά,
Αχιλλέας
-
panosgl2006
- Δημοσιεύσεις: 15
- Εγγραφή: Κυρ Ιουν 06, 2021 11:41 am
Re: ΘΑΛΗΣ 2022
Καλησπέρα σας!Ως μαθητη της Β λυκείου βρήκα το πρώτο θέμα αρκετά εύκολο ενώ το δεύτερο σαφώς ποιο δύσκολο αλλά δεν ήτανε τρομερά δύσκολο όπως κάποιες άλλες χρονιές.Αυτο που με ξάφνιασε ήταν το θέμα της γεωμετρίας που για μένα τουλάχιστον ήταν αρκετά απαιτητικο.Καλα αποτελέσματα!
Re:ΘΑΛΗΣ 2022
ΘΕΜΑ 2-Β' ΛΥΚΕΙΟΥ (Ένας διαφορετικος τροπος-Έτσι το έλυσα εγω)
Για να ορίζονται οι ,
,  πρέπει x,y
πρέπει x,y 1
1
Έστω x-1=a , y-1=b
Τότε γίνεται 2ab-2a -2b
-2b +a+b
+a+b 0
0
Άρα πρέπει 2ab+a+b 2a
2a +2b
+2b
Αφού 2ab+a+b 0 και 2a
0 και 2a +
+
 0 πρέπει:
0 πρέπει:
 και αρα
και αρα
 ....
....

Από (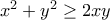 )...
)... [Με ισότητα αν a+b=2ab](1)
[Με ισότητα αν a+b=2ab](1)
Από AM-GM :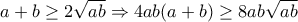 [Με ισότητα αν a=b](2)
[Με ισότητα αν a=b](2)
Άρα
Όμως θέλουμε άρα πρέπει :
άρα πρέπει :
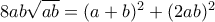
Αυτό για να ισχύει πρέπει να ισχύουν ταυτόχρονα οι ισότητες των ανισοτήτων (1),(2)
Άρα πρέπει: και
και 
Άρα ή
ή  και άρα
και άρα 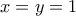 ή
ή 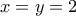
Για να ορίζονται οι
 ,
,  πρέπει x,y
πρέπει x,y 1
1Έστω x-1=a , y-1=b
Τότε γίνεται 2ab-2a
 -2b
-2b +a+b
+a+b 0
0 Άρα πρέπει 2ab+a+b
 2a
2a +2b
+2b
Αφού 2ab+a+b
 0 και 2a
0 και 2a +
+
 0 πρέπει:
0 πρέπει: και αρα
και αρα ....
....
Από (
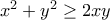 )...
)... [Με ισότητα αν a+b=2ab](1)
[Με ισότητα αν a+b=2ab](1)Από AM-GM :
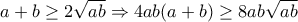 [Με ισότητα αν a=b](2)
[Με ισότητα αν a=b](2)Άρα

Όμως θέλουμε
 άρα πρέπει :
άρα πρέπει :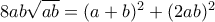
Αυτό για να ισχύει πρέπει να ισχύουν ταυτόχρονα οι ισότητες των ανισοτήτων (1),(2)
Άρα πρέπει:
 και
και 
Άρα
 ή
ή  και άρα
και άρα 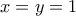 ή
ή 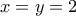
τελευταία επεξεργασία από math. σε Κυρ Νοέμ 13, 2022 5:29 pm, έχει επεξεργασθεί 3 φορές συνολικά.
Re: ΘΑΛΗΣ 2022
Προσοχή νομίζω στο β ερώτημα υπάρχει λάθος γιατί έχετε πάρει οτι η ΑΒ=α το οποίο δεν ισχύει γιατί το τρίγωνο ΑΒΓ δεν είναι ισόπλευρο είναι ισοσκελέςHenri van Aubel έγραψε: ↑Σάβ Νοέμ 12, 2022 10:42 amΚαλημέρα και πάλι!!Μία λύση στο ΘΕΜΑ 2 Γ ΓΥΜΝΑΣΙΟΥ.
(1) Τοείναι το περίκεντρο του τριγώνου
οπότε
(2) Προφανώςμε υποτείνουσες
άρα
Συνεπώς
Επιπλέον έχουμε
Άρα τελικά
Λύση Θέμα 2 Γεωμετρία Γ Γυμνασίου
Β ερώτημα
Το Εμβαδόν του τραπεζίου ΑΜΘΔ είναι Ε=(β+Β) U/2
Το β του τραπεζίου είναι ίσο με την πλευρά ΘΔ
Το Β του τραπεζίου είναι ίσο με ΑΜ=υ
Το ύψος του τραπεζίου U είναι ίσο με ΘΜ=ΘΒ+ΒΜ
Συγκρίνω τα τρίγωνα ΘΒΔ και ΑΒΜ
Έχουν ΑΒ=ΒΔ (πλευρές τετραγώνου)
Είναι και τα 2 ορθογώνια
Επίσης γωνία ΔΒΑ + γωνία ΔΒΘ + γωνία ΑΒΜ=1800
Άρα γωνία ΔΒΘ + γωνία ΑΒΜ =900 και
Γωνία ΑΒΜ + γωνία ΒΑΜ =900
Συνεπώς γωνία ΔΒΘ=γωνία ΒΑΜ
‘Άρα τα τρίγωνα ΔΒΘ = ΑΒΜ
Άρα και πλευρά ΘΔ=ΒΜ και πλευρά ΘΒ=ΑΜ=υ
Αφού πλευρά ΒΓ=α τότε ΘΔ=ΒΜ=ΒΓ/2=α/2
Επίσης από τα παραπάνω ΘΜ=υ +α/2
Συνεπώς (ΑΜΘΔ)=(ΘΔ+ΑΜ)ΘΜ/2 = (α/2+υ)(υ+α/2)/2 = (α/2+υ)^(2 )/2
-
Henri van Aubel
- Δημοσιεύσεις: 876
- Εγγραφή: Τρί Σεπ 13, 2022 12:01 pm
- elenipappa
- Δημοσιεύσεις: 10
- Εγγραφή: Πέμ Ιούλ 01, 2021 8:42 pm
- Τοποθεσία: Αθήνα
Re: ΘΑΛΗΣ 2022
Μία λύση για το Π2 Γ γυμνασίου 
1) Αφού το ABDE είναι τετράγωνο, τότε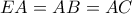 Άρα το
Άρα το 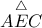 είναι ισοσκελές, άρα
είναι ισοσκελές, άρα 
Επίσης
Ακόμα
Άρα στο

2)
Άρα
Επίσης
Άρα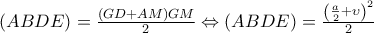
1) Αφού το ABDE είναι τετράγωνο, τότε
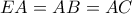 Άρα το
Άρα το 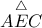 είναι ισοσκελές, άρα
είναι ισοσκελές, άρα 
Επίσης

Ακόμα

Άρα στο


2)

Άρα

Επίσης

Άρα
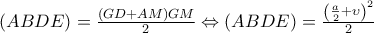
Wer wagt, gewinnt
Re: ΘΑΛΗΣ 2022
Πρόβλημα 1 Α λυκείου
Θέτουμε και
και 
Τότε οι εξισώσεις του συστήματος είναι ισοδύναμες με τις
 και
και 
επομένως και
και 

Άρα και
και 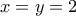
Θέτουμε
 και
και 
Τότε οι εξισώσεις του συστήματος είναι ισοδύναμες με τις
 και
και 
επομένως
 και
και 

Άρα
 και
και 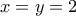
Κανάβης Χρήστος
Μαθηματικός
Μαθηματικός
-
AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ
- Επιμελητής
- Δημοσιεύσεις: 1172
- Εγγραφή: Τετ Δεκ 31, 2008 8:07 pm
- Τοποθεσία: ΗΡΑΚΛΕΙΟ ΚΡΗΤΗΣ
Re: ΘΑΛΗΣ 2022
Για το θέμα με τις καραμέλες.
Έστω η αρχική κατάσταση για Γιώργο, Δημήτρη και σακούλα, ενώ
η αρχική κατάσταση για Γιώργο, Δημήτρη και σακούλα, ενώ  η τελική κατάσταση. Καλούμαστε να αποδείξουμε ότι
η τελική κατάσταση. Καλούμαστε να αποδείξουμε ότι  το οποίο ισοδυναμεί με
το οποίο ισοδυναμεί με  . Η τελευταία σχέση προκύπτει άμεσα από την σχέση
. Η τελευταία σχέση προκύπτει άμεσα από την σχέση  καθώς το άθροισμα των καραμελών του Δημήτρη και της σακούλας ελαττώθηκε.
καθώς το άθροισμα των καραμελών του Δημήτρη και της σακούλας ελαττώθηκε.
Από ότι βλέπω είναι στην ουσία ο β τρόπος του Νίκου του Ράπανου. Καθώς όμως απευθυνόμαστε σε μαθητές Β Γυμνασίου, ο α τρόπος του Νίκου είναι διδακτικά υποδειγματικός! Συγχαρητήρια Νίκο!
Έστω
 η αρχική κατάσταση για Γιώργο, Δημήτρη και σακούλα, ενώ
η αρχική κατάσταση για Γιώργο, Δημήτρη και σακούλα, ενώ  η τελική κατάσταση. Καλούμαστε να αποδείξουμε ότι
η τελική κατάσταση. Καλούμαστε να αποδείξουμε ότι  το οποίο ισοδυναμεί με
το οποίο ισοδυναμεί με  . Η τελευταία σχέση προκύπτει άμεσα από την σχέση
. Η τελευταία σχέση προκύπτει άμεσα από την σχέση  καθώς το άθροισμα των καραμελών του Δημήτρη και της σακούλας ελαττώθηκε.
καθώς το άθροισμα των καραμελών του Δημήτρη και της σακούλας ελαττώθηκε.Από ότι βλέπω είναι στην ουσία ο β τρόπος του Νίκου του Ράπανου. Καθώς όμως απευθυνόμαστε σε μαθητές Β Γυμνασίου, ο α τρόπος του Νίκου είναι διδακτικά υποδειγματικός! Συγχαρητήρια Νίκο!
- elenipappa
- Δημοσιεύσεις: 10
- Εγγραφή: Πέμ Ιούλ 01, 2021 8:42 pm
- Τοποθεσία: Αθήνα
Re: ΘΑΛΗΣ 2022
Γ Λυκείου. Γεωμετρία
Τα σημεία ανήκουν σε ημικύκλιο διαμέτρου
ανήκουν σε ημικύκλιο διαμέτρου  οπότε:
οπότε:
 λόγω διχοτόμου και
λόγω διχοτόμου και 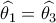 ως εγγεγραμμένες στο ίδιο τόξο (χορδής
ως εγγεγραμμένες στο ίδιο τόξο (χορδής  ) . άρα ,
) . άρα ,  .
Άμεση συνέπεια: Τα σημεία
.
Άμεση συνέπεια: Τα σημεία  ανήκουν σε κύκλο διαμέτρου
ανήκουν σε κύκλο διαμέτρου 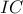 , οπότε
, οπότε  .
.
Ομοίως , δηλαδή τα σημεία
, δηλαδή τα σημεία 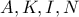 ανήκουν στον κύκλο διαμέτρου ,
ανήκουν στον κύκλο διαμέτρου ,  .
.
Τα σημεία
 ανήκουν σε ημικύκλιο διαμέτρου
ανήκουν σε ημικύκλιο διαμέτρου  οπότε:
οπότε:  λόγω διχοτόμου και
λόγω διχοτόμου και 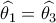 ως εγγεγραμμένες στο ίδιο τόξο (χορδής
ως εγγεγραμμένες στο ίδιο τόξο (χορδής  ) . άρα ,
) . άρα ,  .
Άμεση συνέπεια: Τα σημεία
.
Άμεση συνέπεια: Τα σημεία  ανήκουν σε κύκλο διαμέτρου
ανήκουν σε κύκλο διαμέτρου 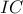 , οπότε
, οπότε  .
.Ομοίως
 , δηλαδή τα σημεία
, δηλαδή τα σημεία 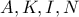 ανήκουν στον κύκλο διαμέτρου ,
ανήκουν στον κύκλο διαμέτρου ,  .
.Re: ΘΑΛΗΣ 2022
Β Λυκείου/ Πρόβλημα 1
Αρχικά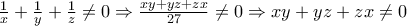 .
.
Από την ταυτότητα Euler έχω ότι:
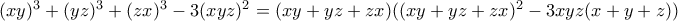
Όμως:
 , οπότε:
, οπότε:


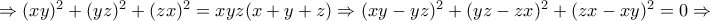
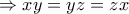 .
.
Επίσης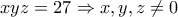 , οπότε
, οπότε  .
.
Τότε .
.
Τελικά .
.
Αρχικά
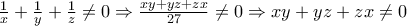 .
.Από την ταυτότητα Euler έχω ότι:

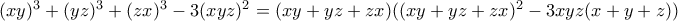
Όμως:

 , οπότε:
, οπότε:

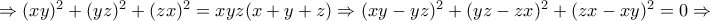
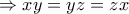 .
.Επίσης
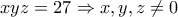 , οπότε
, οπότε  .
.Τότε
 .
.Τελικά
 .
.- S.E.Louridas
- Δημοσιεύσεις: 5956
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
Re: ΘΑΛΗΣ 2022
Ας δούμε και μία άλλη άποψη για τη Γεωμετρία της Β’ Λυκείου και μόνο για λόγους πλουραλισμού.
Το τόξο που τα σημεία του «βλέπουν» την πλευρά υπό γωνία
υπό γωνία  θα τέμνει την πλευρά
θα τέμνει την πλευρά  ας πούμε στο
ας πούμε στο  , οπότε
, οπότε 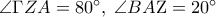 και το τόξο του που τα σημεία του «βλέπουν» τη πλευρά
και το τόξο του που τα σημεία του «βλέπουν» τη πλευρά  υπό γωνία
υπό γωνία  θα τέμνει τη πλευρά
θα τέμνει τη πλευρά  ας πούμε στο σημείο
ας πούμε στο σημείο οπότε
οπότε  Τότε θα έχουμε
Τότε θα έχουμε με αυτό να σημαίνει ότι τα συμμετρικά των ίσων πλευρών
με αυτό να σημαίνει ότι τα συμμετρικά των ίσων πλευρών  ως προς τις ευθείες
ως προς τις ευθείες  αντίστοιχα ταυτίζονται έστω στο ευθύγραμμο τμήμα
αντίστοιχα ταυτίζονται έστω στο ευθύγραμμο τμήμα  Είναι καθαρό ότι
Είναι καθαρό ότι  και ομοίως
και ομοίως 
Έτσι άμεσα επιπλέον παίρνουμε
edit: Τοποθέτηση του σχήματος
Το τόξο που τα σημεία του «βλέπουν» την πλευρά
 υπό γωνία
υπό γωνία  θα τέμνει την πλευρά
θα τέμνει την πλευρά  ας πούμε στο
ας πούμε στο  , οπότε
, οπότε 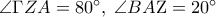 και το τόξο του που τα σημεία του «βλέπουν» τη πλευρά
και το τόξο του που τα σημεία του «βλέπουν» τη πλευρά  υπό γωνία
υπό γωνία  θα τέμνει τη πλευρά
θα τέμνει τη πλευρά  ας πούμε στο σημείο
ας πούμε στο σημείο οπότε
οπότε  Τότε θα έχουμε
Τότε θα έχουμε με αυτό να σημαίνει ότι τα συμμετρικά των ίσων πλευρών
με αυτό να σημαίνει ότι τα συμμετρικά των ίσων πλευρών  ως προς τις ευθείες
ως προς τις ευθείες  αντίστοιχα ταυτίζονται έστω στο ευθύγραμμο τμήμα
αντίστοιχα ταυτίζονται έστω στο ευθύγραμμο τμήμα  Είναι καθαρό ότι
Είναι καθαρό ότι  και ομοίως
και ομοίως 
Έτσι άμεσα επιπλέον παίρνουμε

edit: Τοποθέτηση του σχήματος
τελευταία επεξεργασία από S.E.Louridas σε Τρί Νοέμ 15, 2022 8:46 am, έχει επεξεργασθεί 2 φορές συνολικά.
S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
- S.E.Louridas
- Δημοσιεύσεις: 5956
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
Re: ΘΑΛΗΣ 2022
Για το πρώτο της Α’ Λυκείου και μόνο για λόγους πολυφωνίας.
Θεωρούμε οπότε έχουμε:
οπότε έχουμε: 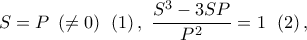 άρα από τις
άρα από τις  προκύπτει απλά ότι
προκύπτει απλά ότι  και
και 
Επίσης επιλύεται και αν θέσουμε με
με  διάφορο προφανώς από το μηδέν κτλ.
διάφορο προφανώς από το μηδέν κτλ.
Αναφέρθηκα σε γνωστές μεθόδους δουλειάς που ενίοτε διδάσκουμε.
Ας μου επιτραπεί και μία προσωπική τοποθέτηση.
Η επιτροπή διαγωνισμών της Ε.Μ.Ε. σε μία πολύ δύσκολη εποχή και με μαθητές προερχόμενους από κακή τριετία τουλάχιστον ως προς το σωστό κτίσιμο των βασικών γνώσεων, με ιώσεις με προβληματικές τηλεδιδασκαλίες, από οικογένειες με οικονομικά προβλήματα και τα λοιπά γνωστά που ποδηγέτησαν με κακό τρόπο τη γνώση, χωρίς την ευθύνη των διδασκόντων και στηριζόμενη η επιτροπή στην εντιμότητα των συναδέλφων επιτηρητών έκανε με το παραπάνω το πολύ δύσκολο καθήκον της με καλά θέματα με πλουραλισμό λύσεων για ένα μαθητή που ενδιαφέρεται για το άθλημα. Είναι πολύ δύσκολο το έργο μίας τέτοιας επιστημονικής επιτροπής κάτω από τόσο κακές συνθήκες.
Θεωρούμε
 οπότε έχουμε:
οπότε έχουμε: 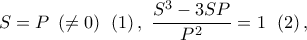 άρα από τις
άρα από τις  προκύπτει απλά ότι
προκύπτει απλά ότι  και
και 
Επίσης επιλύεται και αν θέσουμε
 με
με  διάφορο προφανώς από το μηδέν κτλ.
διάφορο προφανώς από το μηδέν κτλ.Αναφέρθηκα σε γνωστές μεθόδους δουλειάς που ενίοτε διδάσκουμε.
Ας μου επιτραπεί και μία προσωπική τοποθέτηση.
Η επιτροπή διαγωνισμών της Ε.Μ.Ε. σε μία πολύ δύσκολη εποχή και με μαθητές προερχόμενους από κακή τριετία τουλάχιστον ως προς το σωστό κτίσιμο των βασικών γνώσεων, με ιώσεις με προβληματικές τηλεδιδασκαλίες, από οικογένειες με οικονομικά προβλήματα και τα λοιπά γνωστά που ποδηγέτησαν με κακό τρόπο τη γνώση, χωρίς την ευθύνη των διδασκόντων και στηριζόμενη η επιτροπή στην εντιμότητα των συναδέλφων επιτηρητών έκανε με το παραπάνω το πολύ δύσκολο καθήκον της με καλά θέματα με πλουραλισμό λύσεων για ένα μαθητή που ενδιαφέρεται για το άθλημα. Είναι πολύ δύσκολο το έργο μίας τέτοιας επιστημονικής επιτροπής κάτω από τόσο κακές συνθήκες.
τελευταία επεξεργασία από S.E.Louridas σε Σάβ Νοέμ 12, 2022 10:53 pm, έχει επεξεργασθεί 2 φορές συνολικά.
S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
Re: ΘΑΛΗΣ 2022
Πρόβλημα 2 Β γυμνασίου
Αφού

το τρίγωνο είναι ισοσκελές άρα γωνία
είναι ισοσκελές άρα γωνία  .
.
Επομένως
 άρα
άρα 
Επίσης έστω γωνία .
.
Άρα γωνία .
.
Τότε
 άρα
άρα 
Επομένως
Β) Έστω τότε
τότε 
Άρα άρα
άρα 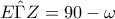
επομένως για το τρίγωνο ΕΖΓ ισχύει

Επίσης είναι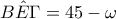 αφού
αφού 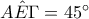 και
και 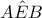

Άρα

άρα το τρίγωνο ΒΖΕ είναι ισοσκελές άρα ΒΖ=ΕΖ
Αφού

το τρίγωνο
 είναι ισοσκελές άρα γωνία
είναι ισοσκελές άρα γωνία  .
.Επομένως
 άρα
άρα 
Επίσης έστω γωνία
 .
. Άρα γωνία
 .
. Τότε

 άρα
άρα 
Επομένως

Β) Έστω
 τότε
τότε 
Άρα
 άρα
άρα 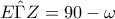
επομένως για το τρίγωνο ΕΖΓ ισχύει

Επίσης είναι
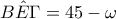 αφού
αφού 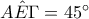 και
και 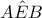

Άρα

άρα το τρίγωνο ΒΖΕ είναι ισοσκελές άρα ΒΖ=ΕΖ
τελευταία επεξεργασία από pana1333 σε Κυρ Νοέμ 13, 2022 9:36 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Κανάβης Χρήστος
Μαθηματικός
Μαθηματικός
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες





 δεν είδα καλά ότι έλεγε
δεν είδα καλά ότι έλεγε