Θέματα της 9ης τάξης για την 2η φάση, 6 Μαρτίου 2022.
1. Οι μη μηδενικοί φυσικοί αριθμοί
 και
και  είναι τέτοιοι, ώστε ο
είναι τέτοιοι, ώστε ο  να διαιρείται με τον
να διαιρείται με τον  για όλους τους μη μηδενικούς φυσικούς
για όλους τους μη μηδενικούς φυσικούς 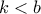 . Να αποδείξετε, ότι ο
. Να αποδείξετε, ότι ο  διαιρείται με τον
διαιρείται με τον  για όλους τους μη μηδενικούς
για όλους τους μη μηδενικούς  . (Α. Κουζνέτσοβ, Τ. Κοροτσένκο)
. (Α. Κουζνέτσοβ, Τ. Κοροτσένκο)2. Στον όμιλο πατριωτικού τραγουδιού συμμετέχουν 12 μαθητές, ο καθένας τους ξέρει μερικά τραγούδια (μπορεί και κανένα). Θα λέμε, ότι μια ομάδα μαθητών ξέρει ένα τραγούδι, αν μπορεί να το τραγουδήσει τουλάχιστον ένας μαθητής της ομάδας. Ο υπεύθυνος του ομίλου διαπίστωσε, ότι οποιαδήποτε ομάδα 10 μαθητών ξέρει ακριβώς 20 τραγούδια και οποιαδήποτε ομάδα 8 μαθητών – ακριβώς 16 τραγούδια. Να αποδείξετε ότι η ομάδα όλων των 12 μαθητών ξέρει ακριβώς 24 τραγούδια. (Β. Μύγκριν, Α. Κουζνέτσοβ)
3. Να αποδείξετε, ότι τα σημεία τομής των απέναντι διχοτόμων ενός τραπεζίου καθώς και τα άκρα οποιασδήποτε βάσης του βρίσκονται στον ίδιο κύκλο. Για λόγους ευκρίνειας θα θεωρήσουμε, ότι τα σημεία είναι τοποθετημένα, όπως στο σχήμα. (Α. Κουζνέτσοβ)
4. Θα λέμε, ότι το σημείο
 βρίσκεται μεταξύ των παραβολών
βρίσκεται μεταξύ των παραβολών 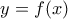 και
και 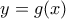 , αν
, αν  . Να βρείτε τον ελάχιστο πραγματικό
. Να βρείτε τον ελάχιστο πραγματικό  , για τον οποίο ισχύει ο παρακάτω ισχυρισμός: οποιοδήποτε τμήμα, τα άκρα και το μέσο του οποίου βρίσκονται μεταξύ των παραβολών
, για τον οποίο ισχύει ο παρακάτω ισχυρισμός: οποιοδήποτε τμήμα, τα άκρα και το μέσο του οποίου βρίσκονται μεταξύ των παραβολών 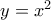 και
και  , εξ ολοκλήρου βρίσκεται μεταξύ των παραβολών
, εξ ολοκλήρου βρίσκεται μεταξύ των παραβολών 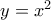 και
και 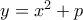 . (Ι. Τούρκυν)
. (Ι. Τούρκυν)Καταληκτική αίθουσα
5. Δίνονται δυο σωροί από βότσαλα: 1703 βότσαλα στον ένα σωρό και 2022 στον άλλο. Η Αλεξάνδρα και η Όλγα παίζουν ένα παιχνίδι, κάνοντας κινήσεις με την σειρά, ξεκινώντας από την Αλεξάνδρα. Έστω πριν την κίνηση μιας παίχτριας οι σωροί έχουν
 και
και  βότσαλα, εξάλλου
βότσαλα, εξάλλου 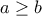 . Τότε με την κίνησή του η κάθε παίχτρια επιτρέπεται να πάρει από το σωρό με
. Τότε με την κίνησή του η κάθε παίχτρια επιτρέπεται να πάρει από το σωρό με  βότσαλα οποιοδήποτε αριθμό βότσαλων από
βότσαλα οποιοδήποτε αριθμό βότσαλων από  έως
έως  . Χάνει αυτή που δεν μπορεί να κάνει κίνηση. Ποια θα κερδίσει αν παίξει σωστά; (Α .Γκολοβάνοβ)
. Χάνει αυτή που δεν μπορεί να κάνει κίνηση. Ποια θα κερδίσει αν παίξει σωστά; (Α .Γκολοβάνοβ)6. Στο τρίγωνο
 φέρουμε την διάμεσο
φέρουμε την διάμεσο  . Στην εφαπτομένη από το σημείο
. Στην εφαπτομένη από το σημείο  προς τον περιγεγραμμένο κύκλο του τριγώνου
προς τον περιγεγραμμένο κύκλο του τριγώνου  δίνεται σημείο
δίνεται σημείο  τέτοιο, ώστε
τέτοιο, ώστε  . Τα τμήματα
. Τα τμήματα  και
και  τέμνονται στο σημείο
τέμνονται στο σημείο  . Να αποδείξετε, ότι το κέντρο του περιγεγραμμένου κύκλου του τριγώνου
. Να αποδείξετε, ότι το κέντρο του περιγεγραμμένου κύκλου του τριγώνου 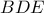 βρίσκεται στην ευθεία
βρίσκεται στην ευθεία  . (Α. Κουζνέτσοβ)
. (Α. Κουζνέτσοβ)7. Δίνονται
 διαφορετικοί μη μηδενικοί φυσικοί αριθμοί, οποιοιδήποτε δυο εκ των οποίων προκύπτουν ο ένας από των άλλων με μετάθεση των ψηφίων τους ( το μηδέν δεν μπορεί να τοποθετηθεί στην πρώτη θέση). Για ποιο μέγιστο
διαφορετικοί μη μηδενικοί φυσικοί αριθμοί, οποιοιδήποτε δυο εκ των οποίων προκύπτουν ο ένας από των άλλων με μετάθεση των ψηφίων τους ( το μηδέν δεν μπορεί να τοποθετηθεί στην πρώτη θέση). Για ποιο μέγιστο  όλοι αυτοί οι αριθμοί μπορούν να διαιρούνται με τον μικρότερο από αυτούς; (Τ. Κοροτσένκο)
όλοι αυτοί οι αριθμοί μπορούν να διαιρούνται με τον μικρότερο από αυτούς; (Τ. Κοροτσένκο)Πηγή: Επίσημη σελίδα της ολυμπιάδας.

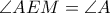 .
.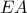 και η εφαπτομένη στο σημείο
και η εφαπτομένη στο σημείο  .
. και
και ,
, είναι
είναι και άρα
και άρα
 , δηλαδή ότι
, δηλαδή ότι  . Επομένως, αρκεί να δείξουμε ότι
. Επομένως, αρκεί να δείξουμε ότι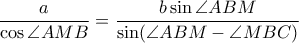
 η προβολή του
η προβολή του  στην
στην  το συμμετρικό του
το συμμετρικό του  ως προς το
ως προς το  και
και  το σημείο τέτοιο ώστε το τετράπλευρο
το σημείο τέτοιο ώστε το τετράπλευρο  να είναι παραλληλόγραμμο. Τότε, είναι
να είναι παραλληλόγραμμο. Τότε, είναι και
και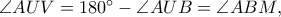




 τέμνονται πάνω στην
τέμνονται πάνω στην  .
.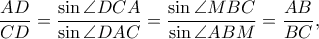
 το σημείο που τέμνονται οι εφαπτομένες του Ισχυρισμού 2, είναι
το σημείο που τέμνονται οι εφαπτομένες του Ισχυρισμού 2, είναι , άρα
, άρα  και
και

 είναι το περίκεντρο του τριγώνου
είναι το περίκεντρο του τριγώνου  , όπως θέλαμε.
, όπως θέλαμε. στο
στο 
 , υπάρχει
, υπάρχει 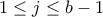 τέτοιο ώστε
τέτοιο ώστε  .
. , υπάρχει
, υπάρχει  τέτοιο ώστε
τέτοιο ώστε 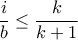 (αν τέτοιο
(αν τέτοιο  δεν υπήρχε, τότε
δεν υπήρχε, τότε
 οπότε
οπότε  και
και  λόγω της ελαχιστότητας του
λόγω της ελαχιστότητας του 
 , επιλέγουμε το
, επιλέγουμε το  του Ισχυρισμού και αφού
του Ισχυρισμού και αφού  είναι
είναι  , οπότε
, οπότε  και άρα
και άρα  όπως θέλαμε.
όπως θέλαμε. ως
ως  και
και 
 .
.  με
με  είναι θέση ήττας αν και μόνο αν
είναι θέση ήττας αν και μόνο αν 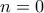 ή
ή 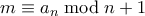 . Αρκεί να δείξουμε ότι από κάθε θέση ήττας δεν μπορούμε να πάμε σε θέση νίκης, ενώ από θέση νίκης μπορούμε οπωσδήποτε να πάμε σε θέση ήττας.
. Αρκεί να δείξουμε ότι από κάθε θέση ήττας δεν μπορούμε να πάμε σε θέση νίκης, ενώ από θέση νίκης μπορούμε οπωσδήποτε να πάμε σε θέση ήττας.  . Αν ισχύει επιπλέον ότι
. Αν ισχύει επιπλέον ότι  , τότε όλες αυτές είναι θέσεις ήττας αφού
, τότε όλες αυτές είναι θέσεις ήττας αφού 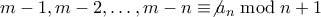 .
. για κάποιο
για κάποιο  . Πρέπει να δείξουμε ότι τα
. Πρέπει να δείξουμε ότι τα  είναι όλες θέσεις νίκης. Αλλά αν το
είναι όλες θέσεις νίκης. Αλλά αν το  ήταν θέση ήττας για κάποιο
ήταν θέση ήττας για κάποιο  , τότε θα είχαμε
, τότε θα είχαμε  . Αυτό όμως, από τον ορισμό του
. Αυτό όμως, από τον ορισμό του  , θα μας έδινε
, θα μας έδινε  . Ισχύει όμως και
. Ισχύει όμως και  αφού στην περίπτωση που εξετάζουμε ισχύει ότι
αφού στην περίπτωση που εξετάζουμε ισχύει ότι  .
.  μέγιστο ώστε
μέγιστο ώστε  και
και  . Πρέπει
. Πρέπει  αφού τουλάχιστον ένα από τα
αφού τουλάχιστον ένα από τα  είναι ισότιμο με
είναι ισότιμο με  και αυτό δεν μπορεί να είναι το
και αυτό δεν μπορεί να είναι το  . Αν
. Αν  , τότε το
, τότε το  είναι θέση ήττας και μπορούμε να πάμε από το
είναι θέση ήττας και μπορούμε να πάμε από το  και μπορούμε να πάμε από το
και μπορούμε να πάμε από το  το οποίο είναι θέση ήττας. Πράγματι, από τον ορισμό του
το οποίο είναι θέση ήττας. Πράγματι, από τον ορισμό του  που μας λέει ότι το
που μας λέει ότι το 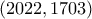 είναι θέση ήττας ή όχι.
είναι θέση ήττας ή όχι.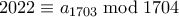 , το οποίο δίνει
, το οποίο δίνει  . Αλλά τότε έχουμε
. Αλλά τότε έχουμε  το οποίο δίνει
το οποίο δίνει  . Άρα
. Άρα  το οποίο δίνει
το οποίο δίνει  . Παίρνουμε έπειτα
. Παίρνουμε έπειτα  που δίνει
που δίνει  . Μετά
. Μετά 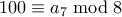 που δίνει
που δίνει 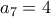 . Τέλος παίρνουμε
. Τέλος παίρνουμε  που δίνει
που δίνει  . Μόνο που είναι εύκολο να ελεγχθεί ότι
. Μόνο που είναι εύκολο να ελεγχθεί ότι  .
.  το συμμετρικό του
το συμμετρικό του 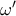 ο συμμετρικός του περιγεγραμμένου κύκλου
ο συμμετρικός του περιγεγραμμένου κύκλου  του τριγώνου
του τριγώνου  .
.  τα δεύτερα σημεία τομής της ευθείας της διαμέσου
τα δεύτερα σημεία τομής της ευθείας της διαμέσου  , και
, και  είναι παραλληλόγραμμα.
είναι παραλληλόγραμμα. .
. είναι η ευθεία της
είναι η ευθεία της  . Θα αποδείξουμε ότι η ευθεία
. Θα αποδείξουμε ότι η ευθεία  εφάπτεται του περιγεγραμμένου κύκλου
εφάπτεται του περιγεγραμμένου κύκλου  .
.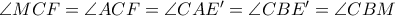 .
. .
. .
.
 . Έστω τώρα ότι η ευθεία
. Έστω τώρα ότι η ευθεία  ,
,  στο σημείο
στο σημείο  (ως εγγεγραμμένες γωνίες του κύκλου
(ως εγγεγραμμένες γωνίες του κύκλου  ).
).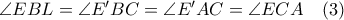 . Από
. Από  και
και  έχουμε ότι
έχουμε ότι  , δηλαδή, το τετράπλευρο
, δηλαδή, το τετράπλευρο  είναι εγγράψιμο, οπότε
είναι εγγράψιμο, οπότε  , δηλαδή,
, δηλαδή,  .
. εφάπτεται του
εφάπτεται του  .
. .
.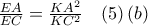 , και
, και  .
.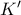 .
. , και
, και  .
. , επομένως,
, επομένως,  , και
, και  .
. και
και  εχουμε ότι
εχουμε ότι  , δηλαδή το
, δηλαδή το  , δηλαδή,
, δηλαδή,  .
.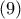 προκύπτει από την ομοιότητα των τριγώνων
προκύπτει από την ομοιότητα των τριγώνων  .
. ή της
ή της  βλέπε
βλέπε  .
.  . Θεωρούμε τα σημεία
. Θεωρούμε τα σημεία  και
και  με
με 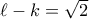 και
και  , οπότε το μέσον του
, οπότε το μέσον του  είναι το
είναι το 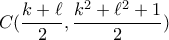 , και είναι εύκολα
, και είναι εύκολα  , οπότε πρέπει κάθε σημείο του τμήματος
, οπότε πρέπει κάθε σημείο του τμήματος  που εύκολα επαληθεύουμε ότι ανήκει στο
που εύκολα επαληθεύουμε ότι ανήκει στο  .
.
 . Αρκεί να δείξουμε ότι για
. Αρκεί να δείξουμε ότι για  και
και  τα άκρα του ευθύγραμμου τμήματος
τα άκρα του ευθύγραμμου τμήματος  είναι ομόσημα ισχύει το ζητούμενο (ένα απλό σχήμα το επιβεβαιώνει ότι τότε ισχύει το ζητούμενο ακόμα και με
είναι ομόσημα ισχύει το ζητούμενο (ένα απλό σχήμα το επιβεβαιώνει ότι τότε ισχύει το ζητούμενο ακόμα και με 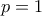 ). Υποθέτουμε λοιπόν ότι
). Υποθέτουμε λοιπόν ότι  . Ισχύουν:
. Ισχύουν: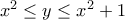 ,
,  και
και .
. , για κάποιο
, για κάποιο 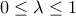 .
. .
. .
.


 .
. και
και  με
με 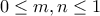 , και
, και
 .
. .
. , τότε το τριώνυμο ως προς
, τότε το τριώνυμο ως προς  διατηρεί πρόσημο που είναι θετικό αφού
διατηρεί πρόσημο που είναι θετικό αφού  .
. , τότε έχει δύο ρίζες
, τότε έχει δύο ρίζες  .
. , οι ρίζες είναι ομόσημες. Αν είναι και οι δύο αρνητικές, τότε στο διάστημα
, οι ρίζες είναι ομόσημες. Αν είναι και οι δύο αρνητικές, τότε στο διάστημα ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) το πρόσημο του τριωνύμου είναι θετικό, όπως θέλαμε. Αν είναι και οι δύο θετικές, τότε για να δείξουμε την ζητούμενη ανισότητα αρκεί να δείξουμε ότι ισχύει για
το πρόσημο του τριωνύμου είναι θετικό, όπως θέλαμε. Αν είναι και οι δύο θετικές, τότε για να δείξουμε την ζητούμενη ανισότητα αρκεί να δείξουμε ότι ισχύει για ![\lambda = \dfrac{m+n+(x-z)^2-1}{2(x-z)^2} \in [0,1] \lambda = \dfrac{m+n+(x-z)^2-1}{2(x-z)^2} \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/0fcccbe40d44da3d202676c8e61695de.png) .
. , δηλαδή ισοδύναμα
, δηλαδή ισοδύναμα  .
.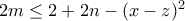 και άρα
και άρα .
. με
με  . Αυτή είναι γνησίως φθίνουσα για
. Αυτή είναι γνησίως φθίνουσα για  και γνησίως αύξουσα για
και γνησίως αύξουσα για 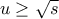 . Άρα, αν
. Άρα, αν ![u \in [r,t] u \in [r,t]](/forum/ext/geomar/texintegr/latexrender/pictures/4e1823259391069132dcd7a3fe004261.png) , για να δείξουμε πως
, για να δείξουμε πως 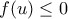 , πρέπει να το δείξουμε για
, πρέπει να το δείξουμε για  ,
,  και
και 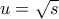 .
. και για
και για  , το οποίο είναι εύκολο με πράξεις.
, το οποίο είναι εύκολο με πράξεις.