Παραθέτω τα θέματα.
Καλή επιτυχία στους Έλληνες και Κύπριους μαθητές
Καλή δύναμη στον Αλέξανδρο Συγκελάκη (αρχηγός) και Θάνο Μάγκο (υπαρχηγός) με την διόρθωση.
Πρόβλημα 1.
Έστω
 ένα οξυγώνιο τρίγωνο τέτοιο, ώστε
ένα οξυγώνιο τρίγωνο τέτοιο, ώστε  με περιγεγραμμένο κύκλο
με περιγεγραμμένο κύκλο  κέντρου
κέντρου  . Έστω
. Έστω  και
και  οι εφαπτομένες του
οι εφαπτομένες του  στα σημεία
στα σημεία  και
και  αντίστοιχα, οι οποίες τέμνονται στο
αντίστοιχα, οι οποίες τέμνονται στο  . Έστω
. Έστω  το ίχνος της καθέτου από το σημείο
το ίχνος της καθέτου από το σημείο  στο ευθύγραμμο τμήμα
στο ευθύγραμμο τμήμα  . Η παράλληλη από το σημείο
. Η παράλληλη από το σημείο  προς την ευθεία
προς την ευθεία  τέμνει την
τέμνει την  στο σημείο
στο σημείο  . Να δείξετε ότι η ευθεία
. Να δείξετε ότι η ευθεία  διέρχεται από το μέσο του ευθύγραμμου τμήματος
διέρχεται από το μέσο του ευθύγραμμου τμήματος  .
. Πρόβλημα 2.
Έστω
 και
και  θετικοί ακέραιοι με
θετικοί ακέραιοι με  τέτοιοι, ώστε να ισχύουν τα εξής:
τέτοιοι, ώστε να ισχύουν τα εξής:(i) ο αριθμός
 διαιρεί τον
διαιρεί τον  ,
,(ii) ο αριθμός
 διαιρεί τον
διαιρεί τον  ,
,(iii) ο αριθμός
 διαιρεί τον
διαιρεί τον  .
.Να αποδείξετε ότι υπάρχει ένα υποσύνολο
 του συνόλου των θετικών διαιρετών του αριθμού
του συνόλου των θετικών διαιρετών του αριθμού  τέτοιο, ώστε το άθροισμα των στοιχείων του
τέτοιο, ώστε το άθροισμα των στοιχείων του  να διαιρείται από το
να διαιρείται από το  αλλά όχι από το
αλλά όχι από το  .
. Πρόβλημα 3.
Να βρείτε όλες τις συναρτήσεις
 τέτοιες, ώστε
τέτοιες, ώστε 
για κάθε
 .
. Πρόβλημα 4.
Ένα τετράγωνο διαστάσεων
 διαιρείται σε
διαιρείται σε  μοναδιαία τετραγωνάκια, όπου
μοναδιαία τετραγωνάκια, όπου  είναι ένας δεδομένος περιττός θετικός ακέραιος. Αρχικά, ο Διόνυσος χρωματίζει κάθε τετραγωνάκι κόκκινο ή μπλε. Ένας βάτραχος μπορεί να πηδήξει από ένα τετραγωνάκι σε ένα άλλο αν και μόνο αν αυτά έχουν το ίδιο χρώμα και επιπλέον τουλάχιστον μία κοινή κορυφή. Μετά, ο Ξανθίας παρατηρεί τον χρωματισμό των τετραγώνων και έπειτα τοποθετεί
είναι ένας δεδομένος περιττός θετικός ακέραιος. Αρχικά, ο Διόνυσος χρωματίζει κάθε τετραγωνάκι κόκκινο ή μπλε. Ένας βάτραχος μπορεί να πηδήξει από ένα τετραγωνάκι σε ένα άλλο αν και μόνο αν αυτά έχουν το ίδιο χρώμα και επιπλέον τουλάχιστον μία κοινή κορυφή. Μετά, ο Ξανθίας παρατηρεί τον χρωματισμό των τετραγώνων και έπειτα τοποθετεί  βάτραχους στα τετραγωνάκια με τέτοιο τρόπο, ώστε σε κάθε ένα από τα
βάτραχους στα τετραγωνάκια με τέτοιο τρόπο, ώστε σε κάθε ένα από τα  τετραγωνάκια κάποιος βάτραχος να μπορεί να φτάσει με πεπερασμένου πλήθους (πιθανόν και μηδέν) πηδήματα. Να βρείτε την ελάχιστη τιμή του
τετραγωνάκια κάποιος βάτραχος να μπορεί να φτάσει με πεπερασμένου πλήθους (πιθανόν και μηδέν) πηδήματα. Να βρείτε την ελάχιστη τιμή του  για την οποία αυτό είναι πάντοτε δυνατό ανεξάρτητα από τον χρωματισμό που επέλεξε ο Διόνυσος.
για την οποία αυτό είναι πάντοτε δυνατό ανεξάρτητα από τον χρωματισμό που επέλεξε ο Διόνυσος.
 το σημείο τομής της
το σημείο τομής της  το σημείο τομής της
το σημείο τομής της  και της
και της  είναι η
είναι η  , ενώ το
, ενώ το  και
και  .
.  ανήκουν σε κύκλο
ανήκουν σε κύκλο  διαμέτρου
διαμέτρου  . Έτσι, αφού το
. Έτσι, αφού το  είναι το ύψος προς την υποτείνουσα στο ορθογώνιο τρίγωνο
είναι το ύψος προς την υποτείνουσα στο ορθογώνιο τρίγωνο  και το τετράπλευρο
και το τετράπλευρο  είναι εγγράψιμο, είναι
είναι εγγράψιμο, είναι 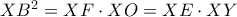 (από τη δύναμη του σημείου
(από τη δύναμη του σημείου  , οπότε
, οπότε  . Άρα
. Άρα .
. και
και  έπεται ότι
έπεται ότι  ,
, .
. είναι παράλληλη στην
είναι παράλληλη στην  , και συνεπώς η
, και συνεπώς η  είναι παράλληλη στην
είναι παράλληλη στην  , όπου
, όπου  είναι το σημείο τομής της
είναι το σημείο τομής της  , όπως θέλαμε.
, όπως θέλαμε. το σημείο τομής του κύκλου και της
το σημείο τομής του κύκλου και της  ,
,  των
των 
 προκύπτουν τα εξής :
προκύπτουν τα εξής :
 είναι εγγράψιμα, αφού
είναι εγγράψιμα, αφού  κάθετα στα
κάθετα στα  αντίστοιχα. Έπεται πως
αντίστοιχα. Έπεται πως  εγγράψιμο , άρα
εγγράψιμο , άρα  Επομένως
Επομένως  εγγράψιμο.
εγγράψιμο. . Όμως επίσης
. Όμως επίσης  . Άρα
. Άρα  , και αφού
, και αφού  το μέσο του
το μέσο του  , προκύπτει το ζητούμενο
, προκύπτει το ζητούμενο είναι κάθετη στη χορδή
είναι κάθετη στη χορδή  είναι διάμεσος στο τρίγωνο
είναι διάμεσος στο τρίγωνο  . Αν η
. Αν η 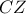 στο
στο  , αφού η
, αφού η  ,
,  ,
, 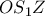 ,
,  είναι ορθές, κι έτσι, το τετράπλευρο
είναι ορθές, κι έτσι, το τετράπλευρο  θα είναι εγγράψιμο, όπως ακριβώς και το
θα είναι εγγράψιμο, όπως ακριβώς και το  . Από το γεγονός αυτό, απορρέει ότι το τετράπλευρο
. Από το γεγονός αυτό, απορρέει ότι το τετράπλευρο  είναι εγγράψιμο (από τη δύναμη του σημείου Χ ως προς τα τετράπλευρα
είναι εγγράψιμο (από τη δύναμη του σημείου Χ ως προς τα τετράπλευρα 

 (από τη δοθείσα παραλληλία) και
(από τη δοθείσα παραλληλία) και 
 (σχέση εγγεγραμμένης γωνίας-γωνίας από χορδή κι εφαπτομένη). Όμως
(σχέση εγγεγραμμένης γωνίας-γωνίας από χορδή κι εφαπτομένη). Όμως 
 και η
και η  η τομή της
η τομή της  ,
,  οι τομές της
οι τομές της 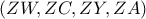 να είναι αρμονική, ή αλλιώς η τετράδα
να είναι αρμονική, ή αλλιώς η τετράδα  να είναι αρμονική.
να είναι αρμονική.  , οπότε αρκεί
, οπότε αρκεί  . Επειδή
. Επειδή  , μπορούμε να θέσουμε
, μπορούμε να θέσουμε 
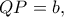

 , οπότε η ζητούμενη γράφεται
, οπότε η ζητούμενη γράφεται 
 είναι αρμονική και άρα:
είναι αρμονική και άρα:
 , μπορούμε να πάρουμε
, μπορούμε να πάρουμε  ώστε
ώστε  , οπότε
, οπότε
 στη δοθείσα, γιa
στη δοθείσα, γιa  και
και  έχουμε:
έχουμε: , και ειδικότερα, για
, και ειδικότερα, για  κ.ο.κ παίρνουμε
κ.ο.κ παίρνουμε  , όπου
, όπου  .
. τότε για
τότε για  και
και  στην αρχική έχουμε:
στην αρχική έχουμε: , όπου για μεγάλα
, όπου για μεγάλα  , οπότε η μονοτονία της συνάρτησης δίνει:
, οπότε η μονοτονία της συνάρτησης δίνει: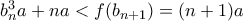 , δηλαδή
, δηλαδή  που είναι άτοπο αφού η
που είναι άτοπο αφού η  πάει στο άπειρο.
πάει στο άπειρο. τότε η
τότε η  , οπότε η μονοτονία της
, οπότε η μονοτονία της  δίνει:
δίνει: για κάθε
για κάθε  και άρα για
και άρα για  για κάθε
για κάθε  για κάθε θετικό ακέραιο
για κάθε θετικό ακέραιο 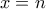 στην αρχική, όπου
στην αρχική, όπου  , όπου
, όπου  , άρα
, άρα  για κάθε θετικό ακέραιο
για κάθε θετικό ακέραιο  με
με 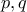 θετικούς ακέραιους. Από την τελευταία σχέση έχουμε
θετικούς ακέραιους. Από την τελευταία σχέση έχουμε  .
. για κάθε θετικό ρητό
για κάθε θετικό ρητό  για κάθε θετικό πραγματικό
για κάθε θετικό πραγματικό  .
.