ΙΜΟ 2021
Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
Re: ΙΜΟ 2021
Θα ήθελα να κάνω μερικές παρατηρήσεις - παραινέσεις διαβάζοντας και τα μηνύματα παραπάνω
1) Για το ερώτημα αν πρέπει να συμμετέχουμε σε διαγωνισμούς η απάντηση είναι βεβαίως. Ο καθένας έχει την οπτική πάνω σε αυτό εγώ προσωπικά θεωρώ ότι η ανίχνευση ταλέντων είναι σημαντική γιατί τα ταλέντα δημιουργούν κεφάλαιο πνευματικό το οποίο μετατρέπεται και σε οικονομικό για την χώρα. Δείτε τους χιλιάδες νέους που έχουν φύγει και μεγαλουργούν στο εξωτερικό.
2) Για το θέμα των υποδομών θεωρώ ότι η δημιουργία ειδικών σχολείων η Ακαδημιών που θα έχουν curriculum τέτοιο που θα στηρίζει τέτοια ταλέντα είναι απαραίτητη.Φυσικά, και η επιλογή διδασκόντων σε αυτά θα γίνεται μετά από αξιοκρατική αξιολόγηση.
3)Η διδασκαλία των Μαθηματικών στο Δημοτικό πρέπει να γίνεται από Μαθηματικούς.
4) Ίσως θα πρέπει να ενθαρρυνθεί η συμμέτοχη των γυναικών στα Μαθηματικά . Δεν μπορεί σε μια χώρα οπού οι γυναίκες είναι η πλειοψηφία να μην υπάρχει ούτε μια στην ΙΜΟ.
5)Οι συμμετέχοντες σε διεθνείς διαγωνισμούς θα μπορούσαν να απαλλάσσονται από τις Πανελλήνιες και να εισάγονται στη σχολή που επιθυμούν άνευ εξετάσεων.
6) H προπόνηση μαζί με τις ομάδες άλλων χωρών θα βοηθούσε στην ανταλλαγή εμπειριών και στρατηγικών.
7) H δημιουργία σειράς βιβλίων η ακόμα και φυλλαδίων που θα βοηθούν το problem solving απο το Γυμνάσιο μέχρι το Λύκειο και θα διατίθενται δωρεάν στο διαδίκτυο.
8)Η οικονομική κατάσταση αρκετών μαθητών μπορεί να τους αποθαρρύνει από συμμέτοχες σε διαγωνισμούς για αυτό η θέσπιση κίνητρων όπως υποτροφίες η και χρηματικά έπαθλα για την κατάκτηση μεταλλίων ίσως είναι απαραίτητη. Δεν μπορεί να δίνουμε 5000 ευρώ την Βδομάδα στον παίκτη ενός τηλεοπτικού παιχνιδιού σαν κοινωνία και να μην προσφέρουμε ανάλογα κίνητρα σε μαθητές.
Τέλος, για να εμπνέουμε τον σεβασμό πρέπει και εμείς να είμαστε τίμιοι, αξιοκρατικοί και διαφανείς.
1) Για το ερώτημα αν πρέπει να συμμετέχουμε σε διαγωνισμούς η απάντηση είναι βεβαίως. Ο καθένας έχει την οπτική πάνω σε αυτό εγώ προσωπικά θεωρώ ότι η ανίχνευση ταλέντων είναι σημαντική γιατί τα ταλέντα δημιουργούν κεφάλαιο πνευματικό το οποίο μετατρέπεται και σε οικονομικό για την χώρα. Δείτε τους χιλιάδες νέους που έχουν φύγει και μεγαλουργούν στο εξωτερικό.
2) Για το θέμα των υποδομών θεωρώ ότι η δημιουργία ειδικών σχολείων η Ακαδημιών που θα έχουν curriculum τέτοιο που θα στηρίζει τέτοια ταλέντα είναι απαραίτητη.Φυσικά, και η επιλογή διδασκόντων σε αυτά θα γίνεται μετά από αξιοκρατική αξιολόγηση.
3)Η διδασκαλία των Μαθηματικών στο Δημοτικό πρέπει να γίνεται από Μαθηματικούς.
4) Ίσως θα πρέπει να ενθαρρυνθεί η συμμέτοχη των γυναικών στα Μαθηματικά . Δεν μπορεί σε μια χώρα οπού οι γυναίκες είναι η πλειοψηφία να μην υπάρχει ούτε μια στην ΙΜΟ.
5)Οι συμμετέχοντες σε διεθνείς διαγωνισμούς θα μπορούσαν να απαλλάσσονται από τις Πανελλήνιες και να εισάγονται στη σχολή που επιθυμούν άνευ εξετάσεων.
6) H προπόνηση μαζί με τις ομάδες άλλων χωρών θα βοηθούσε στην ανταλλαγή εμπειριών και στρατηγικών.
7) H δημιουργία σειράς βιβλίων η ακόμα και φυλλαδίων που θα βοηθούν το problem solving απο το Γυμνάσιο μέχρι το Λύκειο και θα διατίθενται δωρεάν στο διαδίκτυο.
8)Η οικονομική κατάσταση αρκετών μαθητών μπορεί να τους αποθαρρύνει από συμμέτοχες σε διαγωνισμούς για αυτό η θέσπιση κίνητρων όπως υποτροφίες η και χρηματικά έπαθλα για την κατάκτηση μεταλλίων ίσως είναι απαραίτητη. Δεν μπορεί να δίνουμε 5000 ευρώ την Βδομάδα στον παίκτη ενός τηλεοπτικού παιχνιδιού σαν κοινωνία και να μην προσφέρουμε ανάλογα κίνητρα σε μαθητές.
Τέλος, για να εμπνέουμε τον σεβασμό πρέπει και εμείς να είμαστε τίμιοι, αξιοκρατικοί και διαφανείς.
Λέξεις Κλειδιά:
Re: ΙΜΟ 2021
Al.Koutsouridis έγραψε: ↑Τετ Ιούλ 21, 2021 11:14 amΠρόβλημα 3. Έστωένα εσωτερικό σημείο του οξυγώνιου τριγώνου
με
έτσι ώστε
. Το σημείο
του τμήματος
ικανοποιεί την ισότητα
, το σημείο
του τμήματος
ικανοποιεί την ισότητα
και το σημείο
της ευθείας
ικανοποιεί την ισότητα
. Έστω
και
τα περίκεντρα των τριγώνων
και
, αντίστοιχα. Να αποδείξετε ότι οι ευθείες
, και
περνούν από το ίδιο σημείο.
Καταπληκτικό πρόβλημα!
Ας υποθέσουμε ότι οι ευθείες
 και
και  τέμνονται στο
τέμνονται στο  και οι κύκλοι
και οι κύκλοι  και
και  τέμνονται για δεύτερη φορά στο
τέμνονται για δεύτερη φορά στο  . Θα αποδείξουμε ότι τα σημεία
. Θα αποδείξουμε ότι τα σημεία  ,
, και
και  είναι συνευθειακά, δηλαδή ότι το
είναι συνευθειακά, δηλαδή ότι το  ισαπέχει από τα
ισαπέχει από τα  και
και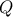 .
.Θα ξεκινήσω με τη απόδειξη δύο βασικών ισχυρισμών:
Ισχυρισμός 1 Τα σημεία
 ,
, ,
, και
και  είναι ομοκυκλικά
είναι ομοκυκλικά Έστω
 το ισογώνιο συζυγές σημείο του
το ισογώνιο συζυγές σημείο του ως προς το
ως προς το  .
.Ισχύει:


Συνεπώς

Έτσι:

Άρα το τετράπλευρο
 είναι εγγράψιμο.
είναι εγγράψιμο.Παρόμοια:


άρα

Επομένως:

Έτσι το τετράπλευρο
 είναι επίσης εγγράψιμο.
είναι επίσης εγγράψιμο.Παίρνοντας δύναμη του σημείου
 ως προς τον
ως προς τον  έχουμε:
έχουμε:
Αντίστοιχα, παίρνοντας δύναμη του
 ως προς τον
ως προς τον  λαμβάνουμε:
λαμβάνουμε:
Συνεπώς, ισχύει:

άρα τα σημεία
 ,
, ,
, και
και  είναι ομοκυκλικά .
είναι ομοκυκλικά . 
Σημείωση: Για τον ορισμό του
 μπορείτε να δείτε εδώ: http://users.math.uoc.gr/~pamfilos/gGal ... ation.html.
μπορείτε να δείτε εδώ: http://users.math.uoc.gr/~pamfilos/gGal ... ation.html.Ισχυρισμός 2 Οι περιγεγραμμένοι κύκλοι των τριγώνων
 και
και  εφάπτονται εξωτερικά στο
εφάπτονται εξωτερικά στο  .
.Ισχύει

Εφόσον όμως
 και
και  έχουμε:
έχουμε:
Επειδή
 λαμβάνουμε ότι:
λαμβάνουμε ότι: .
. Αν η
 τέμνει την
τέμνει την 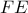 στο
στο  , ισχύει
, ισχύει  και
και 
δηλαδή τα τρίγωνα
 και
και  είναι όμοια άρα
είναι όμοια άρα 
Έτσι

Επομένως
 , άρα οι κύκλοι
, άρα οι κύκλοι  και
και  εφάπτονται.
εφάπτονται. 
Από τον ισχυρισμό 1 το
 έχει ίσες δυνάμεις ως τους
έχει ίσες δυνάμεις ως τους  και
και  εφόσον
εφόσον 
άρα ανήκει στον ριζικό τους άξονα.
Συνεπώς η
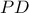 είναι η κοινή τους εσωτερική εφαπτομένη, δηλαδή ισχύει:
είναι η κοινή τους εσωτερική εφαπτομένη, δηλαδή ισχύει:
Μένει, λοιπόν, ν.δ.ο και
 .
.Θα επανέλθω με τη συνέχεια της απόδειξης.
Ματθαίος Κουκλέρης
Re: ΙΜΟ 2021
Συνεχίζουμε με την απόδειξη 2 ακόμη ισχυρισμών.
Έστω . Το
. Το  είναι το σημείο
είναι το σημείο  του πλήρους τετραπλεύρου
του πλήρους τετραπλεύρου  , έτσι εφόσον το τετράπλευρο
, έτσι εφόσον το τετράπλευρο  είναι εγράψιμο, εύκολα προκύπτει ότι τα σημεία
είναι εγράψιμο, εύκολα προκύπτει ότι τα σημεία  ,
, και
και  είναι συνευθειακά, άρα ισχύει
είναι συνευθειακά, άρα ισχύει  .
.
Ισχυρισμός 3 Τα σημεία ,
,  ,
,  και
και  είναι ομοκυκλικά.
είναι ομοκυκλικά.
Ισχύει
Άρα από το ισοσκελές λαμβάνουμε:
λαμβάνουμε:

Από το εγγεγραμμένο τετράπλευρο έχουμε:
έχουμε:

Άρα το τετράπλευρο είναι εγγράψιμο.
είναι εγγράψιμο. 
Ισχυρισμός 4 Οι κύκλοι ,
,  και
και  είναι ομοαξονικοί.
είναι ομοαξονικοί.
Έστω
Από τον ισχυρισμό 3 ισχύει
Όμως άρα
άρα  .
.
Συνεπώς, το έχει ίσες δυνάμεις ως προς τους
έχει ίσες δυνάμεις ως προς τους  και
και  , δηλαδή ανήκει στον ριζικό τους άξονα
, δηλαδή ανήκει στον ριζικό τους άξονα  .
.
Από το εγγεγραμμένο τετράπλευρο παίρνουμε:
παίρνουμε:

Από το εγγεγραμμένο τετράπλευρο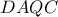 έχουμε:
έχουμε:

Έτσι , άρα ο κύκλος
, άρα ο κύκλος  διέρχεται από το
διέρχεται από το  .
. 
Έστω
 . Το
. Το  είναι το σημείο
είναι το σημείο  του πλήρους τετραπλεύρου
του πλήρους τετραπλεύρου  , έτσι εφόσον το τετράπλευρο
, έτσι εφόσον το τετράπλευρο  είναι εγράψιμο, εύκολα προκύπτει ότι τα σημεία
είναι εγράψιμο, εύκολα προκύπτει ότι τα σημεία  ,
, και
και  είναι συνευθειακά, άρα ισχύει
είναι συνευθειακά, άρα ισχύει  .
.Ισχυρισμός 3 Τα σημεία
 ,
,  ,
,  και
και  είναι ομοκυκλικά.
είναι ομοκυκλικά.Ισχύει

Άρα από το ισοσκελές
 λαμβάνουμε:
λαμβάνουμε:
Από το εγγεγραμμένο τετράπλευρο
 έχουμε:
έχουμε:
Άρα το τετράπλευρο
 είναι εγγράψιμο.
είναι εγγράψιμο. 
Ισχυρισμός 4 Οι κύκλοι
 ,
,  και
και  είναι ομοαξονικοί.
είναι ομοαξονικοί.Έστω

Από τον ισχυρισμό 3 ισχύει

Όμως
 άρα
άρα  .
.Συνεπώς, το
 έχει ίσες δυνάμεις ως προς τους
έχει ίσες δυνάμεις ως προς τους  και
και  , δηλαδή ανήκει στον ριζικό τους άξονα
, δηλαδή ανήκει στον ριζικό τους άξονα  .
.Από το εγγεγραμμένο τετράπλευρο
 παίρνουμε:
παίρνουμε: 
Από το εγγεγραμμένο τετράπλευρο
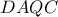 έχουμε:
έχουμε: 
Έτσι
 , άρα ο κύκλος
, άρα ο κύκλος  διέρχεται από το
διέρχεται από το  .
. 
Ματθαίος Κουκλέρης
Re: ΙΜΟ 2021
Επανέρχομαι με την ολοκλήρωση της απόδειξης.
Ισχυρισμός 4 Οι περιγεγραμμένοι κύκλοι των τριγώνων και
και  εφάπτονται εσωτερικά στο
εφάπτονται εσωτερικά στο  .
.
Εφόσον δείξαμε ότι ισχύει , οι κύκλοι
, οι κύκλοι  και
και 
εφάπτονται στο άρα
άρα 
Επίσης, ισχύει:
Από το εγγεγραμμένο τετράπλευρο λαμβάνουμε:
λαμβάνουμε:

Επομένως:

Ας υποθέσουμε ότι ισχύει

που ισχύει.
Συνεπώς:
Από το τρίγωνο παίρνουμε:
παίρνουμε: 
Άρα:
Έτσι, οι κύκλοι και
και  εφάπτονται.
εφάπτονται.
Ισχυρισμός 6 Το σημείο ανήκει στη μεσοκάθετο του
ανήκει στη μεσοκάθετο του  .
.
Δεδομένου ότι τα σημεία ,
, ,
,  και
και  είναι ομοκυκλικά ισχύει:
είναι ομοκυκλικά ισχύει:
 , άρα το P έχει ίσες δυνάμεις ως προς τους
, άρα το P έχει ίσες δυνάμεις ως προς τους  και
και  , δηλαδή ανήκει στον ριζικό τους άξονα που θα είναι η κοινή τους εφαπτομένη.
, δηλαδή ανήκει στον ριζικό τους άξονα που θα είναι η κοινή τους εφαπτομένη.
Συνεπώς .
.
Το ζητούμενο έπεται.
Ισχυρισμός 4 Οι περιγεγραμμένοι κύκλοι των τριγώνων
 και
και  εφάπτονται εσωτερικά στο
εφάπτονται εσωτερικά στο  .
.Εφόσον δείξαμε ότι ισχύει
 , οι κύκλοι
, οι κύκλοι  και
και 
εφάπτονται στο
 άρα
άρα 
Επίσης, ισχύει:

Από το εγγεγραμμένο τετράπλευρο
 λαμβάνουμε:
λαμβάνουμε:
Επομένως:

Ας υποθέσουμε ότι ισχύει

που ισχύει.
Συνεπώς:

Από το τρίγωνο
 παίρνουμε:
παίρνουμε: 
Άρα:

Έτσι, οι κύκλοι
 και
και  εφάπτονται.
εφάπτονται.Ισχυρισμός 6 Το σημείο
 ανήκει στη μεσοκάθετο του
ανήκει στη μεσοκάθετο του  .
.Δεδομένου ότι τα σημεία
 ,
, ,
,  και
και  είναι ομοκυκλικά ισχύει:
είναι ομοκυκλικά ισχύει: , άρα το P έχει ίσες δυνάμεις ως προς τους
, άρα το P έχει ίσες δυνάμεις ως προς τους  και
και  , δηλαδή ανήκει στον ριζικό τους άξονα που θα είναι η κοινή τους εφαπτομένη.
, δηλαδή ανήκει στον ριζικό τους άξονα που θα είναι η κοινή τους εφαπτομένη.Συνεπώς
 .
.Το ζητούμενο έπεται.

Ματθαίος Κουκλέρης
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες
