ΑΡΧΙΜΗΔΗΣ 2021
Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
-
nikolasxen
- Δημοσιεύσεις: 1
- Εγγραφή: Τρί Ιουν 22, 2021 2:32 pm
-
petrosmani
- Δημοσιεύσεις: 22
- Εγγραφή: Τετ Φεβ 24, 2021 6:09 pm
Re: ΑΡΧΙΜΗΔΗΣ 2021
Τελικά θα σταλθούν τα μετάλλια σε καθένα ξεχωριστά ή θα πραγματοποιηθεί τελετή βράβευσης?
- Al.Koutsouridis
- Δημοσιεύσεις: 1797
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Re: ΑΡΧΙΜΗΔΗΣ 2021
Μπορεί κάποιος να ανεβάσει τα θέματα ή να αναφέρει ποια από την sortlist ήταν; Έχει περάσει η προθεσμία. Καλά αποτελέσματα στις ελληνικές εθνικές ομάδες.
Re: ΑΡΧΙΜΗΔΗΣ 2021
Α3 G3 C2 N5Al.Koutsouridis έγραψε: ↑Τετ Ιούλ 21, 2021 11:09 amΜπορεί κάποιος να ανεβάσει τα θέματα ή να αναφέρει ποια από την sortlist ήταν; Έχει περάσει η προθεσμία. Καλά αποτελέσματα στις ελληνικές εθνικές ομάδες.
Re: ΑΡΧΙΜΗΔΗΣ 2021
Ανεβάζω τα πρώτα δύο των μεγάλων προς το παρόν που τα έχω έτοιμα:Al.Koutsouridis έγραψε: ↑Τετ Ιούλ 21, 2021 11:09 amΜπορεί κάποιος να ανεβάσει τα θέματα ή να αναφέρει ποια από την sortlist ήταν; Έχει περάσει η προθεσμία. Καλά αποτελέσματα στις ελληνικές εθνικές ομάδες.
Πρόβλημα 1. Έστω
 θετικοί πραγματικοί αριθμοί τέτοιοι ώστε
θετικοί πραγματικοί αριθμοί τέτοιοι ώστε 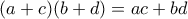 . Να προσδιορίσετε την ελάχιστη δυνατή τιμή της παράστασης
. Να προσδιορίσετε την ελάχιστη δυνατή τιμή της παράστασης
Πρόβλημα 2. Έστω
 κυρτό τετράπλευρο με
κυρτό τετράπλευρο με  ,
, 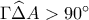 και
και  . Έστω
. Έστω  και
και  τα συμμετρικά του
τα συμμετρικά του  ως προς τις ευθείες
ως προς τις ευθείες  και
και  , αντίστοιχα. Υποθέτουμε ότι τα τμήματα
, αντίστοιχα. Υποθέτουμε ότι τα τμήματα  και
και  τέμνουν την ευθεία
τέμνουν την ευθεία  στα σημεία
στα σημεία  και
και  , αντίστοιχα. Να αποδείξετε ότι οι περιγεγραμμένοι κύκλοι των τριγώνων
, αντίστοιχα. Να αποδείξετε ότι οι περιγεγραμμένοι κύκλοι των τριγώνων  και
και 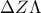 εφάπτονται μεταξύ τους.
εφάπτονται μεταξύ τους.Φιλικά,
Αχιλλέας
Re: ΑΡΧΙΜΗΔΗΣ 2021
Από την Ανισότητα Αριθμητικού- Γεωμετρικού Μέσου (AM-GM) έχουμε ότι:
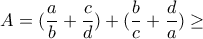


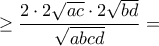
 ,
,με την ισότητα να πιάνεται για
 .
.Re: ΑΡΧΙΜΗΔΗΣ 2021
Λύση: Θέτουμε
 και
και 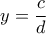 . Τότε
. Τότε  και
και  , και η δοθείσα σχέση
, και η δοθείσα σχέση  δίνει
δίνει
Αφού διαιρέσουμε και τα δύο μέλη με
 και εφαρμόσουμε την την επιμεριστική ιδιότητα παίρνουμε
και εφαρμόσουμε την την επιμεριστική ιδιότητα παίρνουμε
Από την ανισότητα ΑΜ-ΓΜ παίρνουμε
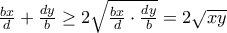 και
και 
Έτσι
 Έχουμε
Έχουμε
Η ισότητα ισχύει εάν
 και
και  , δηλ. εάν
, δηλ. εάν  και
και  . Τότε η δοθείσα σχέση γράφεται
. Τότε η δοθείσα σχέση γράφεται  , που δίνει
, που δίνει 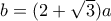 ή
ή  .
. Συνεπώς, η ελάχιστη δυνατή τιμή της παράστασης είναι 8, η οποία λαμβάνεται για όλες τις τετράδες
 της μορφής
της μορφής  και
και  με
με 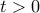 .
.-
petrosmani
- Δημοσιεύσεις: 22
- Εγγραφή: Τετ Φεβ 24, 2021 6:09 pm
Re: ΑΡΧΙΜΗΔΗΣ 2021
Ναι. Δείτε μια παραλλαγή εδώ.petrosmani έγραψε: ↑Πέμ Ιούλ 22, 2021 2:23 pmΣτο 1 πρόβλημα των μικρών 8 είναι η απάντηση όπως και στους μεγάλους ?
Re: ΑΡΧΙΜΗΔΗΣ 2021
Λύση: Έστωachilleas έγραψε: ↑Πέμ Ιούλ 22, 2021 4:21 am..
Πρόβλημα 2. Έστωκυρτό τετράπλευρο με
,
και
. Έστω
και
τα συμμετρικά του
ως προς τις ευθείες
και
, αντίστοιχα. Υποθέτουμε ότι τα τμήματα
και
τέμνουν την ευθεία
στα σημεία
και
, αντίστοιχα. Να αποδείξετε ότι οι περιγεγραμμένοι κύκλοι των τριγώνων
και
εφάπτονται μεταξύ τους.
..
 το συμμετρικό του σημείου
το συμμετρικό του σημείου  ως προς την
ως προς την  . Έστω
. Έστω  το σημείο τομής της
το σημείο τομής της  με την
με την  και έστω
και έστω  το σημείο τομής της
το σημείο τομής της  με την
με την  . Τότε το
. Τότε το  είναι ύψος, διχοτόμος και διάμεσος στο
είναι ύψος, διχοτόμος και διάμεσος στο  , και ομοίως το
, και ομοίως το  στο
στο  .
.Έχουμε

Συνεπώς, το
 ανήκει στον περιγεγραμμένο κύκλο του
ανήκει στον περιγεγραμμένο κύκλο του  .
. Ομοίως, εάν
 είναι το σημείο τομής της
είναι το σημείο τομής της  και της
και της  είναι
είναι
Άρα, το
 ανήκει και στον περιγεγραμμένο κύκλο του
ανήκει και στον περιγεγραμμένο κύκλο του 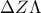 . Συνεπώς, οι περιγεγραμμένοι κύκλοι των τριγώνων
. Συνεπώς, οι περιγεγραμμένοι κύκλοι των τριγώνων  και
και 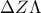 τέμνονται στο
τέμνονται στο  . Για να δείξουμε ότι εφάπτονται σε αυτό αρκεί να δείξουμε ότι
. Για να δείξουμε ότι εφάπτονται σε αυτό αρκεί να δείξουμε ότι  , όπου
, όπου  ,
,  είναι τα αντίστοιχα κέντρα τους (βλ. σχήμα).
είναι τα αντίστοιχα κέντρα τους (βλ. σχήμα).Πράγματι, αφού τα ισοσκελή τρίγωνα
 και
και  είναι ίσα, έχουμε
είναι ίσα, έχουμε
Ομοίως,
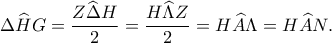
Αφού

έχουμε

στο
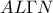 , όπως θέλαμε.
, όπως θέλαμε.- Συνημμένα
-
- archimedes_2021_problem_2_forum.png (44.45 KiB) Προβλήθηκε 2013 φορές
- Lymperis Karras
- Δημοσιεύσεις: 170
- Εγγραφή: Παρ Νοέμ 06, 2020 5:16 pm
Re: ΑΡΧΙΜΗΔΗΣ 2021
Edit: Με πρόλαβε ο κ. Αχιλλέας. Η λύση ήταν σχεδόν ίδια με την δική μου.achilleas έγραψε: ↑Πέμ Ιούλ 22, 2021 4:21 amΠρόβλημα 2. Έστωκυρτό τετράπλευρο με
,
και
. Έστω
και
τα συμμετρικά του
ως προς τις ευθείες
και
, αντίστοιχα. Υποθέτουμε ότι τα τμήματα
και
τέμνουν την ευθεία
στα σημεία
και
, αντίστοιχα. Να αποδείξετε ότι οι περιγεγραμμένοι κύκλοι των τριγώνων
και
εφάπτονται μεταξύ τους.
Φιλικά,
Αχιλλέας
Ένας μαθηματικός χρειάζεται μολύβι, γόμα και μεγάλο καλάθι αχρήστων.
-Hilbert
-Hilbert
-
petrosmani
- Δημοσιεύσεις: 22
- Εγγραφή: Τετ Φεβ 24, 2021 6:09 pm
Re: ΑΡΧΙΜΗΔΗΣ 2021
AAAAAA Ωραία και εγώ τόσο βρήκα αλλά δεν ήξερα αν ηταν σωστο γιατί με μπέρδεψε καθώς χ+1/χ>=2 και ετσι οταν το έλυσα ξανά νόμιζα οτι η απάντηση ειναι το 4. Μπορεί κάποις να μου το εξηγήσει αφου το 4 ειναι μικρότερο απο το 8.achilleas έγραψε: ↑Πέμ Ιούλ 22, 2021 2:40 pmΝαι. Δείτε μια παραλλαγή εδώ.petrosmani έγραψε: ↑Πέμ Ιούλ 22, 2021 2:23 pmΣτο 1 πρόβλημα των μικρών 8 είναι η απάντηση όπως και στους μεγάλους ?
Re: ΑΡΧΙΜΗΔΗΣ 2021
Διότι για να επιτύχουμε τοpetrosmani έγραψε: ↑Πέμ Ιούλ 22, 2021 3:21 pmAAAAAA Ωραία και εγώ τόσο βρήκα αλλά δεν ήξερα αν ηταν σωστο γιατί με μπέρδεψε καθώς χ+1/χ>=2 και ετσι οταν το έλυσα ξανά νόμιζα οτι η απάντηση ειναι το 4. Μπορεί κάποις να μου το εξηγήσει αφου το 4 ειναι μικρότερο απο το 8.achilleas έγραψε: ↑Πέμ Ιούλ 22, 2021 2:40 pmΝαι. Δείτε μια παραλλαγή εδώ.petrosmani έγραψε: ↑Πέμ Ιούλ 22, 2021 2:23 pmΣτο 1 πρόβλημα των μικρών 8 είναι η απάντηση όπως και στους μεγάλους ?
 πρέπει όλες οι μεταβλητές να είναι ίσες και τότε δεν ικανοποιείται η συνθήκη που μας δίνεται πάνω.
πρέπει όλες οι μεταβλητές να είναι ίσες και τότε δεν ικανοποιείται η συνθήκη που μας δίνεται πάνω.
τελευταία επεξεργασία από llenny σε Πέμ Ιούλ 22, 2021 3:25 pm, έχει επεξεργασθεί 1 φορά συνολικά.
-
petrosmani
- Δημοσιεύσεις: 22
- Εγγραφή: Τετ Φεβ 24, 2021 6:09 pm
Re: ΑΡΧΙΜΗΔΗΣ 2021
Πρόβλημα 3. Έστω  ένας θετικός ακέραιος. Οι κορυφές ενός κυρτού
ένας θετικός ακέραιος. Οι κορυφές ενός κυρτού  -γωνου
-γωνου  χρωματίζονται με δύο χρώματα, άσπρο και μαύρο και κάθε χρώμα χρησιμοποιείται τουλάχιστον
χρωματίζονται με δύο χρώματα, άσπρο και μαύρο και κάθε χρώμα χρησιμοποιείται τουλάχιστον  φορές. Ένα κυρτό τετράπλευρο, που οι κορυφές του είναι και κορυφές του
φορές. Ένα κυρτό τετράπλευρο, που οι κορυφές του είναι και κορυφές του  , θα ονομάζεται καλό, εάν έχει τρεις κορυφές του ενός χρώματος και μία κορυφή του άλλου χρώματος. Να αποδείξετε ότι υπάρχουν
, θα ονομάζεται καλό, εάν έχει τρεις κορυφές του ενός χρώματος και μία κορυφή του άλλου χρώματος. Να αποδείξετε ότι υπάρχουν  καλά κυρτά τετράπλευρα που είναι ανά δύο ξένα, δηλαδή ανά δύο δεν έχουν κοινά σημεία στην περίμετρο ή στο εσωτερικό τους.
καλά κυρτά τετράπλευρα που είναι ανά δύο ξένα, δηλαδή ανά δύο δεν έχουν κοινά σημεία στην περίμετρο ή στο εσωτερικό τους.
 ένας θετικός ακέραιος. Οι κορυφές ενός κυρτού
ένας θετικός ακέραιος. Οι κορυφές ενός κυρτού  -γωνου
-γωνου  χρωματίζονται με δύο χρώματα, άσπρο και μαύρο και κάθε χρώμα χρησιμοποιείται τουλάχιστον
χρωματίζονται με δύο χρώματα, άσπρο και μαύρο και κάθε χρώμα χρησιμοποιείται τουλάχιστον  φορές. Ένα κυρτό τετράπλευρο, που οι κορυφές του είναι και κορυφές του
φορές. Ένα κυρτό τετράπλευρο, που οι κορυφές του είναι και κορυφές του  , θα ονομάζεται καλό, εάν έχει τρεις κορυφές του ενός χρώματος και μία κορυφή του άλλου χρώματος. Να αποδείξετε ότι υπάρχουν
, θα ονομάζεται καλό, εάν έχει τρεις κορυφές του ενός χρώματος και μία κορυφή του άλλου χρώματος. Να αποδείξετε ότι υπάρχουν  καλά κυρτά τετράπλευρα που είναι ανά δύο ξένα, δηλαδή ανά δύο δεν έχουν κοινά σημεία στην περίμετρο ή στο εσωτερικό τους.
καλά κυρτά τετράπλευρα που είναι ανά δύο ξένα, δηλαδή ανά δύο δεν έχουν κοινά σημεία στην περίμετρο ή στο εσωτερικό τους.Σιλουανός Μπραζιτίκος
Re: ΑΡΧΙΜΗΔΗΣ 2021
Θα χρησιμοποιήσουμε επαγωγή. Αρχικά γιαsilouan έγραψε: ↑Πέμ Ιούλ 22, 2021 5:17 pmΠρόβλημα 3. Έστωένας θετικός ακέραιος. Οι κορυφές ενός κυρτού
-γωνου
χρωματίζονται με δύο χρώματα, άσπρο και μαύρο και κάθε χρώμα χρησιμοποιείται τουλάχιστον
φορές. Ένα κυρτό τετράπλευρο, που οι κορυφές του είναι και κορυφές του
, θα ονομάζεται καλό, εάν έχει τρεις κορυφές του ενός χρώματος και μία κορυφή του άλλου χρώματος. Να αποδείξετε ότι υπάρχουν
καλά κυρτά τετράπλευρα που είναι ανά δύο ξένα, δηλαδή ανά δύο δεν έχουν κοινά σημεία στην περίμετρο ή στο εσωτερικό τους.
 έχουμε ένα πεντάγωνο
έχουμε ένα πεντάγωνο  με τουλάχιστον 1 άσπρη και τουλάχιστον 1 μαύρη κορυφή. Αρκεί να εξετάσουμε τις περιπτώσεις 1 άσπρης και 4 μαύρων κορυφών, και 2 άσπρων και 3 μαύρων κορυφών. Στην πρώτη περίπτωση υπάρχει καλό τετράπλευρο με τη μια άσπρη κορυφή και 3 από τις 4 μαύρες, ενώ στη δεύτερη υπάρχει καλό τετράπλευρο με 1 από τις 2 άσπρες κορυφές και τις 3 μαύρες.
με τουλάχιστον 1 άσπρη και τουλάχιστον 1 μαύρη κορυφή. Αρκεί να εξετάσουμε τις περιπτώσεις 1 άσπρης και 4 μαύρων κορυφών, και 2 άσπρων και 3 μαύρων κορυφών. Στην πρώτη περίπτωση υπάρχει καλό τετράπλευρο με τη μια άσπρη κορυφή και 3 από τις 4 μαύρες, ενώ στη δεύτερη υπάρχει καλό τετράπλευρο με 1 από τις 2 άσπρες κορυφές και τις 3 μαύρες.Πάμε τώρα στο επαγωγικό βήμα. Έστω
 και
και  το πλήθος των άσπρων και των μαύρων κορυφών αντίστοιχα. Χωρίς βλάβη της γενικότητας, έστω
το πλήθος των άσπρων και των μαύρων κορυφών αντίστοιχα. Χωρίς βλάβη της γενικότητας, έστω 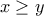 . Τότε έχουμε
. Τότε έχουμε  και
και  . Θα δείξουμε πως υπάρχουν 4 διαδοχικές κορυφές που σχηματίζουν καλό τετράπλευρο με 3 άσπρες κορυφές. Αν
. Θα δείξουμε πως υπάρχουν 4 διαδοχικές κορυφές που σχηματίζουν καλό τετράπλευρο με 3 άσπρες κορυφές. Αν  , για κάθε
, για κάθε  ορίζουμε
ορίζουμε  αν η
αν η  είναι άσπρη και
είναι άσπρη και  διαφορετικά, και στη συνέχεια ορίζουμε
διαφορετικά, και στη συνέχεια ορίζουμε 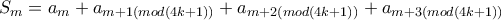 , οπότε το ζητούμενο σύνολο 4 διαδοχικών κορυφών σχηματίζεται αν
, οπότε το ζητούμενο σύνολο 4 διαδοχικών κορυφών σχηματίζεται αν  για κάποιο
για κάποιο  . Παρατηρούμε ότι τα
. Παρατηρούμε ότι τα 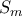 και
και 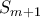 διαφέρουν πάντα το πολύ κατά 1, ενώ
διαφέρουν πάντα το πολύ κατά 1, ενώ  για κάθε
για κάθε  , οπότε ο μόνος τρόπος να μην υπάρχει
, οπότε ο μόνος τρόπος να μην υπάρχει  με
με  είναι να έχουμε
είναι να έχουμε 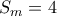 για όλα τα
για όλα τα  , ή να έχουμε
, ή να έχουμε  για κάθε
για κάθε  . Η πρώτη περίπτωση δίνει εύκολα ότι όλες οι κορυφές είναι άσπρες, το οποίο αντιβαίνει στις υποθέσεις του προβλήματος. Στη δεύτερη περίπτωση πάλι έχουμε:
. Η πρώτη περίπτωση δίνει εύκολα ότι όλες οι κορυφές είναι άσπρες, το οποίο αντιβαίνει στις υποθέσεις του προβλήματος. Στη δεύτερη περίπτωση πάλι έχουμε:
και ταυτόχρονα

άτοπο και πάλι. Επομένως, υπάρχει
 με
με  , άρα και 4 διαδοχικές κορυφές που σχηματίζουν καλό τετράπλευρο
, άρα και 4 διαδοχικές κορυφές που σχηματίζουν καλό τετράπλευρο  με 3 άσπρες κορυφές. Σβήνοντας αυτό το καλό τετράπλευρο (τις κορυφές του και κάθε ακμή που διέρχεται από κάποια εξ' αυτών), μένει ένα κυρτό πολύγωνο
με 3 άσπρες κορυφές. Σβήνοντας αυτό το καλό τετράπλευρο (τις κορυφές του και κάθε ακμή που διέρχεται από κάποια εξ' αυτών), μένει ένα κυρτό πολύγωνο  που ικανοποιεί τις υποθέσεις του προβλήματος για
που ικανοποιεί τις υποθέσεις του προβλήματος για 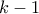 , αφού έχει
, αφού έχει 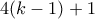 κορυφές, τουλάχιστον
κορυφές, τουλάχιστον 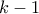 μαύρες κορυφές και τουλάχιστον
μαύρες κορυφές και τουλάχιστον  άσπρες κορυφές. Από την επαγωγική υπόθεση, το
άσπρες κορυφές. Από την επαγωγική υπόθεση, το  έχει
έχει 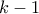 ξένα ανά 2 καλά κυρτά τετράπλευρα, τα οποία δεν τέμνουν το
ξένα ανά 2 καλά κυρτά τετράπλευρα, τα οποία δεν τέμνουν το  (αφού το
(αφού το  δεν τέμνει το
δεν τέμνει το  ), οπότε μαζί με το
), οπότε μαζί με το  έχουμε
έχουμε  ξένα ανά 2 καλά κυρτά τετράπλευρα.
ξένα ανά 2 καλά κυρτά τετράπλευρα.Κολλιοπουλος Νικος.
Μεταδιδακτορικός ερευνητής.
Ερευνητικά ενδιαφέροντα: Στοχαστικές ΜΔΕ, ασυμπτωτική ανάλυση στοχαστικών συστημάτων, εφαρμογές αυτών στα χρηματοοικονομικά και στη διαχείριση ρίσκων.
Μεταδιδακτορικός ερευνητής.
Ερευνητικά ενδιαφέροντα: Στοχαστικές ΜΔΕ, ασυμπτωτική ανάλυση στοχαστικών συστημάτων, εφαρμογές αυτών στα χρηματοοικονομικά και στη διαχείριση ρίσκων.
Re: ΑΡΧΙΜΗΔΗΣ 2021
Για k=1 προφανώς και ισχύει από συνθήκη και από την αρχή της περιστεροφωλιας.silouan έγραψε: ↑Πέμ Ιούλ 22, 2021 5:17 pmΠρόβλημα 3. Έστωένας θετικός ακέραιος. Οι κορυφές ενός κυρτού
-γωνου
χρωματίζονται με δύο χρώματα, άσπρο και μαύρο και κάθε χρώμα χρησιμοποιείται τουλάχιστον
φορές. Ένα κυρτό τετράπλευρο, που οι κορυφές του είναι και κορυφές του
, θα ονομάζεται καλό, εάν έχει τρεις κορυφές του ενός χρώματος και μία κορυφή του άλλου χρώματος. Να αποδείξετε ότι υπάρχουν
καλά κυρτά τετράπλευρα που είναι ανά δύο ξένα, δηλαδή ανά δύο δεν έχουν κοινά σημεία στην περίμετρο ή στο εσωτερικό τους.
Έστω ότι ισχύει για k=n θα δείξουμε ότι ισχύει και για k=n+1.
(Σκοπός μας είναι να δείξουμε πως υπάρχουν 4 διαδοχικές κορυφές οι οποίες αποτελούν καλό τετράπλευρο τότε από το επαγωγικό βήμα έχουμε τελείωση).
Από την αρχή τής περιστεροφωλιας έχουμε ότι ένα χρώμα έχει τουλάχιστον 2n+3 κορυφές έστω μαύρες.
Επιλέγω μια λευκή κορυφή και χωρίς αυτή φτιάχνω n+1 ομάδες διαδοχικών τετράδων κορυφών.
Από την αρχή της περιστεροφωλιας και πάλη έχουμε ότι μια τετράδα περιέχει τουλάχιστον τρεις μαύρες κοριφες.
Αν περιέχει τρεις μαύρες και μια λευκή τελειώσαμε.
Αν και τα 4 έχουν το ίδιο χρώμα τότε κάνουμε ένα "κλικ" δεξιά όπως η φορά του ρολογιού αν είναι 3-1 τελειώσαμε αν είναι πάλη όλα το ίδιο χρώμα το ξανακάνουμε μέχρι να καταλήξουμε σε 3-1 που είναι σίγουρο αφού υπάρχουν και από τα δύο χρώματα.
-
petrosmani
- Δημοσιεύσεις: 22
- Εγγραφή: Τετ Φεβ 24, 2021 6:09 pm
Re: ΑΡΧΙΜΗΔΗΣ 2021
Πρόβλημα 4. Έστω  το σύνολο των φυσικών αριθμών και
το σύνολο των φυσικών αριθμών και  το σύνολο των μη μηδενικών φυσικών αριθμών. Να προσδιορίσετε όλες τις συναρτήσεις
το σύνολο των μη μηδενικών φυσικών αριθμών. Να προσδιορίσετε όλες τις συναρτήσεις  οι οποίες ικανοποιούν και τις τρεις συνθήκες:
οι οποίες ικανοποιούν και τις τρεις συνθήκες:
(α) για ένα τουλάχιστον
για ένα τουλάχιστον 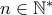 ,
,
(β) για κάθε
για κάθε  ,
,
(γ) υπάρχουν άπειροι θετικοί φυσικοί αριθμοί έτσι ώστε:
έτσι ώστε:  , για όλα τα
, για όλα τα  με
με  .
.
 το σύνολο των φυσικών αριθμών και
το σύνολο των φυσικών αριθμών και  το σύνολο των μη μηδενικών φυσικών αριθμών. Να προσδιορίσετε όλες τις συναρτήσεις
το σύνολο των μη μηδενικών φυσικών αριθμών. Να προσδιορίσετε όλες τις συναρτήσεις  οι οποίες ικανοποιούν και τις τρεις συνθήκες:
οι οποίες ικανοποιούν και τις τρεις συνθήκες:(α)
 για ένα τουλάχιστον
για ένα τουλάχιστον 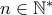 ,
,(β)
 για κάθε
για κάθε  ,
, (γ) υπάρχουν άπειροι θετικοί φυσικοί αριθμοί
 έτσι ώστε:
έτσι ώστε:  , για όλα τα
, για όλα τα  με
με  .
.Re: ΑΡΧΙΜΗΔΗΣ 2021
Απ' όσο θυμάμαι, η δεύτερη συνθήκη είναιachilleas έγραψε: ↑Παρ Ιούλ 23, 2021 9:16 pmΠρόβλημα 4. Έστωτο σύνολο των φυσικών αριθμών και
το σύνολο των μη μηδενικών φυσικών αριθμών. Να προσδιορίσετε όλες τις συναρτήσεις
οι οποίες ικανοποιούν και τις τρεις συνθήκες:
(α)για ένα τουλάχιστον
,
(β)για κάθε
,
(γ) υπάρχουν άπειροι θετικοί φυσικοί αριθμοίέτσι ώστε:
, για όλα τα
με
.
 για κάθε
για κάθε 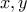
Αρχικά από το β) έχουμε
 , άρα
, άρα 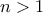 .
. Υποθέτουμε τώρα (χωρίς βλάβη της γενικότητας) ότι
 είναι ο μικρότερος φυσικός τέτοιος ώστε
είναι ο μικρότερος φυσικός τέτοιος ώστε  . Στη συνέχεια, αν
. Στη συνέχεια, αν  είναι η παραγοντοποίηση του
είναι η παραγοντοποίηση του  σε δυνάμεις πρώτων, από το β) έχουμε
σε δυνάμεις πρώτων, από το β) έχουμε  , που σημαίνει ότι
, που σημαίνει ότι  για κάποιο
για κάποιο  . Ισχύει όμως
. Ισχύει όμως  , οπότε από την υπόθεση ελαχίστου πρέπει να έχουμε
, οπότε από την υπόθεση ελαχίστου πρέπει να έχουμε  , που σημαίνει ότι
, που σημαίνει ότι  όπου
όπου  είναι ένας πρώτος.
είναι ένας πρώτος. Θα δείξουμε τώρα ότι
 για κάθε
για κάθε  , όπου
, όπου  ένας θετικός ακέραιος και
ένας θετικός ακέραιος και  είναι η μέγιστη δύναμη του
είναι η μέγιστη δύναμη του  που διαιρεί το
που διαιρεί το  .
.Έστω τώρα
 ένας φυσικός με
ένας φυσικός με  , για όλα τα
, για όλα τα  με
με  . Αν
. Αν  , διαιρώντας το
, διαιρώντας το  με το
με το  έχουμε
έχουμε  με
με  . Μετά, αν είναι
. Μετά, αν είναι  τότε έχουμε
τότε έχουμε 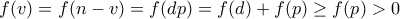 , το οποίο είναι άτοπο διότι
, το οποίο είναι άτοπο διότι 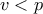 και ο
και ο  είναι ο ελάχιστος
είναι ο ελάχιστος  με
με  . Άρα είναι
. Άρα είναι  και
και 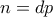 . Μετά για κάθε
. Μετά για κάθε  έχουμε
έχουμε  και άρα
και άρα  δηλαδή
δηλαδή  . Άρα ο
. Άρα ο  έχει την ίδια ιδιότητα με τον
έχει την ίδια ιδιότητα με τον  , οπότε επαναλαμβάνοντας την ίδια διαδικασία βρίσκουμε μια γνησίως φθίνουσα ακολουθία
, οπότε επαναλαμβάνοντας την ίδια διαδικασία βρίσκουμε μια γνησίως φθίνουσα ακολουθία  με
με  , όπου κάθε
, όπου κάθε  έχει την ίδια ιδιότητα με τον
έχει την ίδια ιδιότητα με τον  (η κατασκευή της ακολουθίας μπορεί να συνεχιστεί μέχρι να φτάσουμε σε όρο μικρότερο του
(η κατασκευή της ακολουθίας μπορεί να συνεχιστεί μέχρι να φτάσουμε σε όρο μικρότερο του  , και αυτό πρέπει να συμβεί μετά από πεπερασμένο αριθμό βημάτων καθώς διαφορετικά θα είχαμε μια άπειρη γνησίως φθίνουσα ακολουθία φυσικών αριθμών, πράγμα αδύνατο). Επομένως για
, και αυτό πρέπει να συμβεί μετά από πεπερασμένο αριθμό βημάτων καθώς διαφορετικά θα είχαμε μια άπειρη γνησίως φθίνουσα ακολουθία φυσικών αριθμών, πράγμα αδύνατο). Επομένως για  παίρνουμε
παίρνουμε  , όπου
, όπου  και
και  . Επιπλέον, επειδή υπάρχουν άπειροι φυσικοί
. Επιπλέον, επειδή υπάρχουν άπειροι φυσικοί  με την ιδιότητα γ) και
με την ιδιότητα γ) και 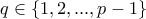 , υπάρχει ένας
, υπάρχει ένας  ώστε τη συγκεκριμένη ιδιότητα να την έχουν άπειροι αριθμοί της μορφής
ώστε τη συγκεκριμένη ιδιότητα να την έχουν άπειροι αριθμοί της μορφής  με
με  , οπότε τελικά όλοι οι αριθμοί αυτής της μορφής (από την κατασκευή της γνησίως φθίνουσας ακολουθίας παραπάνω). Τέλος, επειδή για
, οπότε τελικά όλοι οι αριθμοί αυτής της μορφής (από την κατασκευή της γνησίως φθίνουσας ακολουθίας παραπάνω). Τέλος, επειδή για  με
με  έχουμε
έχουμε  , ισχύει
, ισχύει  , οπότε από το β) έχουμε
, οπότε από το β) έχουμε  , δηλαδή την ιδιότητα γ) την έχουν όλες οι δυνάμεις το
, δηλαδή την ιδιότητα γ) την έχουν όλες οι δυνάμεις το  με θετικό ακέραιο εκθέτη.
με θετικό ακέραιο εκθέτη.Θέτουμε τώρα
 , και για έναν οποιοδήποτε φυσικό
, και για έναν οποιοδήποτε φυσικό  έχουμε
έχουμε  με
με 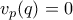 , οπότε από το β) έχουμε
, οπότε από το β) έχουμε  , οπότε αρκεί να δείξουμε ότι
, οπότε αρκεί να δείξουμε ότι  . Έστω πως υπάρχουν φυσικοί r που δεν διαιρούνται με το
. Έστω πως υπάρχουν φυσικοί r που δεν διαιρούνται με το  ώστε
ώστε  , και έστω
, και έστω  ο ελάχιστος αυτών. Τότε, υπάρχει φυσικός
ο ελάχιστος αυτών. Τότε, υπάρχει φυσικός  με
με  , οπότε γράφουμε
, οπότε γράφουμε  με
με  και έχουμε
και έχουμε  , που σημαίνει ότι
, που σημαίνει ότι  (από την υπόθεση ελαχίστου για το
(από την υπόθεση ελαχίστου για το  ). Άρα έχουμε
). Άρα έχουμε  με
με  , οπότε πρέπει
, οπότε πρέπει  και
και  αν
αν  που είναι άτοπο αφού
που είναι άτοπο αφού  . Επομένως
. Επομένως  και
και  , που σημαίνει ότι
, που σημαίνει ότι  που είναι πάλι άτοπο αφού
που είναι πάλι άτοπο αφού  . Άρα έχουμε πράγματι
. Άρα έχουμε πράγματι  οποτεδήποτε ο
οποτεδήποτε ο  δεν διαιρείται με τον
δεν διαιρείται με τον  και άρα
και άρα  για κάθε φυσικό
για κάθε φυσικό  .
.Εύκολα όλες οι συναρτήσεις της παραπάνω μορφής ικανοποιούν τη συνθήκη α) για
 , τη συνθήκη β), και τη συνθήκη γ) για τις δυνάμεις του
, τη συνθήκη β), και τη συνθήκη γ) για τις δυνάμεις του  .
.Κολλιοπουλος Νικος.
Μεταδιδακτορικός ερευνητής.
Ερευνητικά ενδιαφέροντα: Στοχαστικές ΜΔΕ, ασυμπτωτική ανάλυση στοχαστικών συστημάτων, εφαρμογές αυτών στα χρηματοοικονομικά και στη διαχείριση ρίσκων.
Μεταδιδακτορικός ερευνητής.
Ερευνητικά ενδιαφέροντα: Στοχαστικές ΜΔΕ, ασυμπτωτική ανάλυση στοχαστικών συστημάτων, εφαρμογές αυτών στα χρηματοοικονομικά και στη διαχείριση ρίσκων.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες
