Συμπληρωματικός Θαλής 2020-2021
Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
-
Τσιαλας Νικολαος
- Δημοσιεύσεις: 789
- Εγγραφή: Σάβ Ιαν 17, 2015 1:04 pm
Συμπληρωματικός Θαλής 2020-2021
Παραθέτω τα σημερινά θέματα. Καλά αποτελέσματα σε όλα τα παιδιά!
- Συνημμένα
-
- ΘΕΜΑΤΑ ΘΑΛΗ2.pdf
- (513.72 KiB) Μεταφορτώθηκε 620 φορές
τελευταία επεξεργασία από Τσιαλας Νικολαος σε Σάβ Μάιος 15, 2021 12:53 am, έχει επεξεργασθεί 3 φορές συνολικά.
Λέξεις Κλειδιά:
-
Manolis Petrakis
- Δημοσιεύσεις: 204
- Εγγραφή: Τετ Οκτ 07, 2020 3:19 pm
- Τοποθεσία: Αγρίνιο
Re: Συμπληρωματικός Θαλής 2020-2021
Μία λύση για το 1 της Β Λυκείου.
Χρησιμοποιώντας την έχουμε:
έχουμε:
 , το
, το  όταν
όταν  .
.
 , το
, το  όταν
όταν  .
.
 , το
, το  όταν
όταν 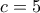 .
.
Άρα .
.
Το ισχύει όταν
ισχύει όταν  η οποία είναι υποχρεωτικά η μοναδική λύση του συστήματος.
η οποία είναι υποχρεωτικά η μοναδική λύση του συστήματος.
Χρησιμοποιώντας την
 έχουμε:
έχουμε: , το
, το  όταν
όταν  .
. , το
, το  όταν
όταν  .
. , το
, το  όταν
όταν 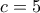 .
.Άρα
 .
.Το
 ισχύει όταν
ισχύει όταν  η οποία είναι υποχρεωτικά η μοναδική λύση του συστήματος.
η οποία είναι υποχρεωτικά η μοναδική λύση του συστήματος.-
Manolis Petrakis
- Δημοσιεύσεις: 204
- Εγγραφή: Τετ Οκτ 07, 2020 3:19 pm
- Τοποθεσία: Αγρίνιο
Re: Συμπληρωματικός Θαλής 2020-2021
Για το 1 της Α Λυκείου.
Θέτουμε και
και 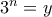 οπότε η δεδομένη γράφεται:
οπότε η δεδομένη γράφεται:
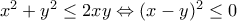 το οποίο ισχύει μόνο αν
το οποίο ισχύει μόνο αν 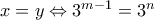 .
.
Άρα με
με  και τελειώσαμε.
και τελειώσαμε.
Θέτουμε
 και
και 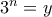 οπότε η δεδομένη γράφεται:
οπότε η δεδομένη γράφεται: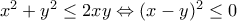 το οποίο ισχύει μόνο αν
το οποίο ισχύει μόνο αν 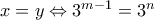 .
.Άρα
 με
με  και τελειώσαμε.
και τελειώσαμε.Re: Συμπληρωματικός Θαλής 2020-2021
Γ' Γυμνασίου- Πρόβλημα 1
Παρατηρούμε ότι: , όπου όλοι οι παράγοντες είναι πρώτοι αριθμοί.
, όπου όλοι οι παράγοντες είναι πρώτοι αριθμοί.
Οι αριθμοί που γράφουμε στη σειρά τότε είναι:
1ος:
2ος:
3ος:
4ος:
5ος: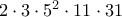
6ος: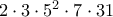
7ος: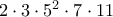
8ος: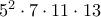
9ος: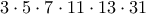
10ος: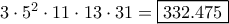
Παρατηρούμε ότι:
 , όπου όλοι οι παράγοντες είναι πρώτοι αριθμοί.
, όπου όλοι οι παράγοντες είναι πρώτοι αριθμοί.Οι αριθμοί που γράφουμε στη σειρά τότε είναι:
1ος:

2ος:

3ος:

4ος:

5ος:
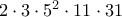
6ος:
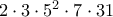
7ος:
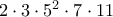
8ος:
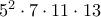
9ος:
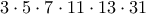
10ος:
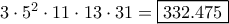
τελευταία επεξεργασία από Joaakim σε Σάβ Μάιος 15, 2021 8:33 am, έχει επεξεργασθεί 1 φορά συνολικά.
Re: Συμπληρωματικός Θαλής 2020-2021
ΘΕΜΑ 2- Α ΛΥΚΕΙΟΥ
Τα δύο μικρότερα αθροίσματα είναι και
και 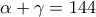 ,
,
ενώ τα δύο μεγαλύτερα αθροίσματα είναι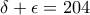 και
και  .
.
Το τρίτο μικρότερο άθροισμα δύο όρων είναι το ή το
ή το  .
.
Αφαιρώντας τις δύο πρώτες σχέσεις κατά μέλη παίρνουμε (*), ενώ από τις δύο τελευταίες παίρνουμε
(*), ενώ από τις δύο τελευταίες παίρνουμε 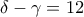
Έτσι,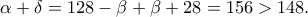
Άρα το τρίτο μικρότερο άθροισμα είναι το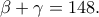 (**)
(**)
Από (*), (**) παίρνουμε και
και  .
.
Εύκολα βρίσκουμε, λοιπόν, ότι
 .
.
Φιλικά,
Αχιλλέας
Τα δύο μικρότερα αθροίσματα είναι
 και
και 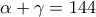 ,
, ενώ τα δύο μεγαλύτερα αθροίσματα είναι
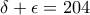 και
και  .
. Το τρίτο μικρότερο άθροισμα δύο όρων είναι το
 ή το
ή το  .
.Αφαιρώντας τις δύο πρώτες σχέσεις κατά μέλη παίρνουμε
 (*), ενώ από τις δύο τελευταίες παίρνουμε
(*), ενώ από τις δύο τελευταίες παίρνουμε 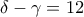
Έτσι,
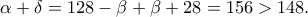
Άρα το τρίτο μικρότερο άθροισμα είναι το
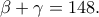 (**)
(**)Από (*), (**) παίρνουμε
 και
και  .
. Εύκολα βρίσκουμε, λοιπόν, ότι
 .
.Φιλικά,
Αχιλλέας
Re: Συμπληρωματικός Θαλής 2020-2021
ΘΕΜΑ 2 - Β ΛΥΚΕΙΟΥ
Έστω ότι ο είναι ένας ακέραιος για τον οποίο υπάρχει πραγματικός αριθμός
είναι ένας ακέραιος για τον οποίο υπάρχει πραγματικός αριθμός  , τέτοιος ώστε
, τέτοιος ώστε  και ο
και ο 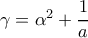 είναι ακέραιος.
είναι ακέραιος.
Tότε είναι ακέραιος αριθμός και η διαφορά
 ,
,
οπότε θα έχουμε για κάποιο μη μηδενικό ακέραιο
για κάποιο μη μηδενικό ακέραιο  .
.
Αφού ,
,
ο αποτελεί ακέραια λύση του πολυωνύμου
αποτελεί ακέραια λύση του πολυωνύμου
 .
.
Με , παίρνουμε
, παίρνουμε  . Αφού ο
. Αφού ο  είναι ακέραιος, o
είναι ακέραιος, o  είναι άρτιος, και ο
είναι άρτιος, και ο  διαιρεί το
διαιρεί το  , άρα
, άρα 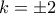 .
.
Παρατηρούμε ότι , αν και μόνο αν
, αν και μόνο αν  . Αυτή η περίπτωση είναι δυνατή με
. Αυτή η περίπτωση είναι δυνατή με  , οπότε
, οπότε 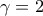 .
.
Επίσης,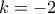 αν και μόνο αν
αν και μόνο αν  . Αυτή η περίπτωση είναι δυνατή εάν
. Αυτή η περίπτωση είναι δυνατή εάν 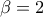 , οπότε
, οπότε  .
.
Συνεπώς, εάν ή
ή 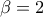 , τότε υπάρχει πραγματικός αριθμός
, τότε υπάρχει πραγματικός αριθμός  τέτοιος ώστε
τέτοιος ώστε  και ο
και ο 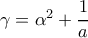 είναι ακέραιος.
είναι ακέραιος.
Σημείωση: Για τον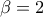 , και
, και 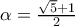 ισχύει
ισχύει  . Για αυτή την τιμή του
. Για αυτή την τιμή του  , ο
, ο  δεν είναι ακέραιος.
δεν είναι ακέραιος.
Φιλικά,
Αχιλλέας
Έστω ότι ο
 είναι ένας ακέραιος για τον οποίο υπάρχει πραγματικός αριθμός
είναι ένας ακέραιος για τον οποίο υπάρχει πραγματικός αριθμός  , τέτοιος ώστε
, τέτοιος ώστε  και ο
και ο 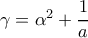 είναι ακέραιος.
είναι ακέραιος.Tότε είναι ακέραιος αριθμός και η διαφορά
 ,
,οπότε θα έχουμε
 για κάποιο μη μηδενικό ακέραιο
για κάποιο μη μηδενικό ακέραιο  .
.Αφού
 ,
, ο
 αποτελεί ακέραια λύση του πολυωνύμου
αποτελεί ακέραια λύση του πολυωνύμου .
.Με
 , παίρνουμε
, παίρνουμε  . Αφού ο
. Αφού ο  είναι ακέραιος, o
είναι ακέραιος, o  είναι άρτιος, και ο
είναι άρτιος, και ο  διαιρεί το
διαιρεί το  , άρα
, άρα 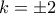 .
.Παρατηρούμε ότι
 , αν και μόνο αν
, αν και μόνο αν  . Αυτή η περίπτωση είναι δυνατή με
. Αυτή η περίπτωση είναι δυνατή με  , οπότε
, οπότε 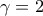 .
.Επίσης,
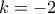 αν και μόνο αν
αν και μόνο αν  . Αυτή η περίπτωση είναι δυνατή εάν
. Αυτή η περίπτωση είναι δυνατή εάν 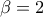 , οπότε
, οπότε  .
.Συνεπώς, εάν
 ή
ή 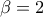 , τότε υπάρχει πραγματικός αριθμός
, τότε υπάρχει πραγματικός αριθμός  τέτοιος ώστε
τέτοιος ώστε  και ο
και ο 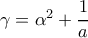 είναι ακέραιος.
είναι ακέραιος.Σημείωση: Για τον
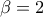 , και
, και 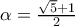 ισχύει
ισχύει  . Για αυτή την τιμή του
. Για αυτή την τιμή του  , ο
, ο  δεν είναι ακέραιος.
δεν είναι ακέραιος. Φιλικά,
Αχιλλέας
- Lymperis Karras
- Δημοσιεύσεις: 170
- Εγγραφή: Παρ Νοέμ 06, 2020 5:16 pm
Re: Συμπληρωματικός Θαλής 2020-2021
Ίδια λύση έχω κι εγώ. Σωστό αποτέλεσμα!
Ένας μαθηματικός χρειάζεται μολύβι, γόμα και μεγάλο καλάθι αχρήστων.
-Hilbert
-Hilbert
Re: Συμπληρωματικός Θαλής 2020-2021
Kαλησπέρα για το πρόβλημα 3 της Α Λυκείου
Τα κόκκινα τμήματα είναι ίσα Αρα
Τα κόκκινα τμήματα είναι ίσα Αρα

- Συνημμένα
-
- Ο Θαλής Α Λυκειίου Πρόβλημα 3.png (38.85 KiB) Προβλήθηκε 4342 φορές
α. Η δυσκολία με κάνει δυνατότερο.
β. Όταν πέφτεις να έχεις τη δύναμη να σηκώνεσαι.
β. Όταν πέφτεις να έχεις τη δύναμη να σηκώνεσαι.
-
Manolis Petrakis
- Δημοσιεύσεις: 204
- Εγγραφή: Τετ Οκτ 07, 2020 3:19 pm
- Τοποθεσία: Αγρίνιο
Re: Συμπληρωματικός Θαλής 2020-2021
Πρόβλημα 2 - Γ' Λυκείου.
Είναι γνωστό ότι .
.
Άρα![S(m,n) = \dfrac{1}{2}[m+(m+2)+(m+4)+...+(m+2n) -m(m+n)] S(m,n) = \dfrac{1}{2}[m+(m+2)+(m+4)+...+(m+2n) -m(m+n)]](/forum/ext/geomar/texintegr/latexrender/pictures/6536ab9bcc9dff44baeb84a7596bafc8.png)
![= \dfrac{1}{2}[m(n+1) +(2+4+6+...+2n)-m(m+n)] = \dfrac{1}{2}[m(n+1) +(2+4+6+...+2n)-m(m+n)]](/forum/ext/geomar/texintegr/latexrender/pictures/1f9f6d01fd053e74ea8790ea66603135.png)
![= \dfrac{1}{2}[m(n+1) +2(1+2+3+...+n)-m(m+n)] = \dfrac{1}{2}[m(n+1) +2(1+2+3+...+n)-m(m+n)]](/forum/ext/geomar/texintegr/latexrender/pictures/466821081502266557c9f76e4d042142.png)
![= \dfrac{1}{2}[m(n+1)+n(n+1)-m(m+n)] = \dfrac{1}{2}[m(n+1)+n(n+1)-m(m+n)]](/forum/ext/geomar/texintegr/latexrender/pictures/ea75eedcc650b750cd230ac14c000c4e.png)
![= \dfrac{1}{2}[(m+n)(n+1)-m(m+n)] = \dfrac{1}{2}[(m+n)(n+1)-m(m+n)]](/forum/ext/geomar/texintegr/latexrender/pictures/1e5a64a8b635aef1ab59abc4353ad6e0.png)
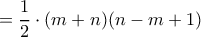
Αν ο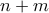 είναι άρτιος τότε ο
είναι άρτιος τότε ο  είναι περιττός, άρα
είναι περιττός, άρα  και είναι αδύνατον ο
και είναι αδύνατον ο  να είναι δύναμη του 2 αφού
να είναι δύναμη του 2 αφού 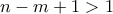 . Ομοίως, αν υποθέσουμε ότι ο
. Ομοίως, αν υποθέσουμε ότι ο 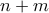 είναι περιττός, τότε
είναι περιττός, τότε  και είναι αδύνατον ο
και είναι αδύνατον ο  να είναι δύναμη του 2.
να είναι δύναμη του 2.
Είναι γνωστό ότι
 .
.Άρα
![S(m,n) = \dfrac{1}{2}[m+(m+2)+(m+4)+...+(m+2n) -m(m+n)] S(m,n) = \dfrac{1}{2}[m+(m+2)+(m+4)+...+(m+2n) -m(m+n)]](/forum/ext/geomar/texintegr/latexrender/pictures/6536ab9bcc9dff44baeb84a7596bafc8.png)
![= \dfrac{1}{2}[m(n+1) +(2+4+6+...+2n)-m(m+n)] = \dfrac{1}{2}[m(n+1) +(2+4+6+...+2n)-m(m+n)]](/forum/ext/geomar/texintegr/latexrender/pictures/1f9f6d01fd053e74ea8790ea66603135.png)
![= \dfrac{1}{2}[m(n+1) +2(1+2+3+...+n)-m(m+n)] = \dfrac{1}{2}[m(n+1) +2(1+2+3+...+n)-m(m+n)]](/forum/ext/geomar/texintegr/latexrender/pictures/466821081502266557c9f76e4d042142.png)
![= \dfrac{1}{2}[m(n+1)+n(n+1)-m(m+n)] = \dfrac{1}{2}[m(n+1)+n(n+1)-m(m+n)]](/forum/ext/geomar/texintegr/latexrender/pictures/ea75eedcc650b750cd230ac14c000c4e.png)
![= \dfrac{1}{2}[(m+n)(n+1)-m(m+n)] = \dfrac{1}{2}[(m+n)(n+1)-m(m+n)]](/forum/ext/geomar/texintegr/latexrender/pictures/1e5a64a8b635aef1ab59abc4353ad6e0.png)
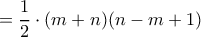
Αν ο
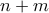 είναι άρτιος τότε ο
είναι άρτιος τότε ο  είναι περιττός, άρα
είναι περιττός, άρα  και είναι αδύνατον ο
και είναι αδύνατον ο  να είναι δύναμη του 2 αφού
να είναι δύναμη του 2 αφού 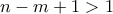 . Ομοίως, αν υποθέσουμε ότι ο
. Ομοίως, αν υποθέσουμε ότι ο 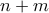 είναι περιττός, τότε
είναι περιττός, τότε  και είναι αδύνατον ο
και είναι αδύνατον ο  να είναι δύναμη του 2.
να είναι δύναμη του 2.- Lymperis Karras
- Δημοσιεύσεις: 170
- Εγγραφή: Παρ Νοέμ 06, 2020 5:16 pm
Re: Συμπληρωματικός Θαλής 2020-2021
Πρόβλημα 2 Γ' Γυμνασίου
α) Για να ισχύει το ζητούμενο θα πρέπει . Άρα το
. Άρα το  ορίζεται μονοσήμαντα
ορίζεται μονοσήμαντα 
β) Μετά από αντικατάσταση του με το
με το  παίρνουμε
παίρνουμε  . Παρατηρούμε πως ισχύει πάντα
. Παρατηρούμε πως ισχύει πάντα 
(με πράξεις καταλήγει τετράγωνο μεγαλύτερο ή ίσο του μηδενός που ισχύει) άρα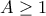 και το ελάχιστο λαμβάνεται για
και το ελάχιστο λαμβάνεται για 
α) Για να ισχύει το ζητούμενο θα πρέπει
 . Άρα το
. Άρα το  ορίζεται μονοσήμαντα
ορίζεται μονοσήμαντα 
β) Μετά από αντικατάσταση του
 με το
με το  παίρνουμε
παίρνουμε  . Παρατηρούμε πως ισχύει πάντα
. Παρατηρούμε πως ισχύει πάντα 
(με πράξεις καταλήγει τετράγωνο μεγαλύτερο ή ίσο του μηδενός που ισχύει) άρα
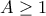 και το ελάχιστο λαμβάνεται για
και το ελάχιστο λαμβάνεται για 
Ένας μαθηματικός χρειάζεται μολύβι, γόμα και μεγάλο καλάθι αχρήστων.
-Hilbert
-Hilbert
- Lymperis Karras
- Δημοσιεύσεις: 170
- Εγγραφή: Παρ Νοέμ 06, 2020 5:16 pm
Re: Συμπληρωματικός Θαλής 2020-2021
Πρόβλημα 3 Γ' Γυμνασίου
Έστω το σημείο τομής της
το σημείο τομής της 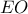 με την
με την  . Λόγω ημικυκλίου το
. Λόγω ημικυκλίου το  έιναι κέντρο του μικρού κύκλου.
έιναι κέντρο του μικρού κύκλου.
Άρα και
και 
Με ΠΘ όμως παίρνουμε ότι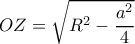
άρα μετά από πράξεις (αντικαθιστώ το στην πρώτη) παίρνω
στην πρώτη) παίρνω 
Για το εμβαδόν εργαζόμαστε ως εξής:
Φέρνουμε την κάθετη

Η συνέχεια είναι εύκολη, θα το ολοκληρώσω αύριο...
Έστω
 το σημείο τομής της
το σημείο τομής της 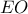 με την
με την  . Λόγω ημικυκλίου το
. Λόγω ημικυκλίου το  έιναι κέντρο του μικρού κύκλου.
έιναι κέντρο του μικρού κύκλου.Άρα
 και
και 
Με ΠΘ όμως παίρνουμε ότι
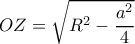
άρα μετά από πράξεις (αντικαθιστώ το
 στην πρώτη) παίρνω
στην πρώτη) παίρνω 
Για το εμβαδόν εργαζόμαστε ως εξής:
Φέρνουμε την κάθετη


Η συνέχεια είναι εύκολη, θα το ολοκληρώσω αύριο...
Ένας μαθηματικός χρειάζεται μολύβι, γόμα και μεγάλο καλάθι αχρήστων.
-Hilbert
-Hilbert
Re: Συμπληρωματικός Θαλής 2020-2021
Γ' Λυκείου- Πρόβλημα 1
Διακρίνουμε δύο περιπτώσεις:
Περίπτωση 1:
Τότε:
 .
.
Όμως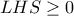 , με το ίσον για
, με το ίσον για 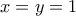 , δεκτή.
, δεκτή.
Περίπτωση 2:
Τότε:
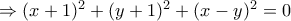 .
.
Όμως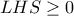 , με το ίσον για
, με το ίσον για  , δεκτή.
, δεκτή.
Τελικά: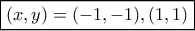 .
.
Διακρίνουμε δύο περιπτώσεις:
Περίπτωση 1:

Τότε:

 .
.Όμως
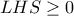 , με το ίσον για
, με το ίσον για 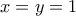 , δεκτή.
, δεκτή.Περίπτωση 2:

Τότε:

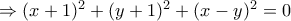 .
.Όμως
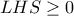 , με το ίσον για
, με το ίσον για  , δεκτή.
, δεκτή.Τελικά:
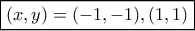 .
.
τελευταία επεξεργασία από Joaakim σε Κυρ Μάιος 16, 2021 1:12 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Re: Συμπληρωματικός Θαλής 2020-2021
ΘΕΜΑ 3 - Β ΛΥΚΕΙΟΥ
(Σχεδιάζουμε το τρίγωνο και τη γωνία
και τη γωνία  με τη φορά των δεικτών του ρολογιού, οπότε παίρνουμε το
με τη φορά των δεικτών του ρολογιού, οπότε παίρνουμε το  να είναι σημείο της πλευράς
να είναι σημείο της πλευράς  )
)
Στο ορθογώνιο τρίγωνο έχουμε
έχουμε  (βλ. Αλγεβρα Β Λυκείου, σελ. 92).
(βλ. Αλγεβρα Β Λυκείου, σελ. 92).
και άρα .
.
Έτσι, (**), οπότε
(**), οπότε 
(**) Αλλιώς: Ο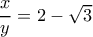 και ο συζυγής του
και ο συζυγής του 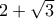 είναι ρίζες της εξίσωσης
είναι ρίζες της εξίσωσης 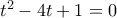 , οπότε
, οπότε  .
.
Έτσι, από το Πυθαγόρειο στο παίρνουμε
παίρνουμε
 .
.
Συνεπώς, στο ορθογώνιο τρίγωνο , η υποτείνουσα έχει διπλάσιο μήκος της κάθετης πλευράς
, η υποτείνουσα έχει διπλάσιο μήκος της κάθετης πλευράς  , οποτε
, οποτε  .
.
Φιλικά,
Αχιλλέας
(Σχεδιάζουμε το τρίγωνο
 και τη γωνία
και τη γωνία  με τη φορά των δεικτών του ρολογιού, οπότε παίρνουμε το
με τη φορά των δεικτών του ρολογιού, οπότε παίρνουμε το  να είναι σημείο της πλευράς
να είναι σημείο της πλευράς  )
)Στο ορθογώνιο τρίγωνο
 έχουμε
έχουμε  (βλ. Αλγεβρα Β Λυκείου, σελ. 92).
(βλ. Αλγεβρα Β Λυκείου, σελ. 92).και άρα
 .
.Έτσι,
 (**), οπότε
(**), οπότε 
(**) Αλλιώς: Ο
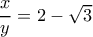 και ο συζυγής του
και ο συζυγής του 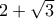 είναι ρίζες της εξίσωσης
είναι ρίζες της εξίσωσης 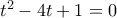 , οπότε
, οπότε  .
.Έτσι, από το Πυθαγόρειο στο
 παίρνουμε
παίρνουμε .
.Συνεπώς, στο ορθογώνιο τρίγωνο
 , η υποτείνουσα έχει διπλάσιο μήκος της κάθετης πλευράς
, η υποτείνουσα έχει διπλάσιο μήκος της κάθετης πλευράς  , οποτε
, οποτε  .
.Φιλικά,
Αχιλλέας
- Συνημμένα
-
- thales_2020b_B2.png (8.04 KiB) Προβλήθηκε 4256 φορές
-
socrates
- Επιμελητής
- Δημοσιεύσεις: 6461
- Εγγραφή: Δευ Μαρ 09, 2009 1:47 pm
- Τοποθεσία: Θεσσαλονίκη
- Επικοινωνία:
Re: Συμπληρωματικός Θαλής 2020-2021
Β,Γ Γυμνασίου Θέμα 1
Βρίσκουμε τον δέκατο μικρότερο διαιρέτη του αριθμού. Οι διαιρέτες του 4654650 είναι οι 1,2,3,5,6,7,10, 11,13,14.
Άρα ο 10ος μεγαλύτερος είναι ο 4654650:14=332475
https://www.wiskundeolympiade.nl/phocad ... ven_en.pdf (Θέμα Β1)
Β Γυμνασίου Θέμα 2
https://mathematica.gr/forum/viewtopic. ... 13#p144713 (Θέμα 4)
Β Γυμνασίου Θέμα 3
https://www.wiskundeolympiade.nl/files/ ... ven_en.pdf (Θέμα Β2)
Γ Γυμνασίου Θέμα 3
https://www.wiskundeolympiade.nl/files/ ... ven_en.pdf (Θέμα Β3)
Α Λυκείου Θέμα 1
viewtopic.php?f=58&t=32205 (Θέμα 2)
Α Λυκείου Θέμα 2
https://www.wiskundeolympiade.nl/files/ ... ven_en.pdf (Θέμα Β1)
Β Λυκείου Θέμα 2
Αφαιρώντας οπότε αντικαθιστώντας στην πρώτη
οπότε αντικαθιστώντας στην πρώτη  οπότε
οπότε 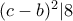 δηλ.
δηλ.  ή
ή 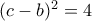 κτλ
κτλ
Γ Λυκείου Θέμα 1
Είναι με ισότητα αν-ν
με ισότητα αν-ν
 δηλαδή αν-ν
δηλαδή αν-ν 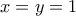 ή
ή 
Γ Λυκείου Θέμα 2
Γενικότερο: search.php?keywords=43&t=12692&sf=msgonly
Βρίσκουμε τον δέκατο μικρότερο διαιρέτη του αριθμού. Οι διαιρέτες του 4654650 είναι οι 1,2,3,5,6,7,10, 11,13,14.
Άρα ο 10ος μεγαλύτερος είναι ο 4654650:14=332475
https://www.wiskundeolympiade.nl/phocad ... ven_en.pdf (Θέμα Β1)
Β Γυμνασίου Θέμα 2
https://mathematica.gr/forum/viewtopic. ... 13#p144713 (Θέμα 4)
Β Γυμνασίου Θέμα 3
https://www.wiskundeolympiade.nl/files/ ... ven_en.pdf (Θέμα Β2)
Γ Γυμνασίου Θέμα 3
https://www.wiskundeolympiade.nl/files/ ... ven_en.pdf (Θέμα Β3)
Α Λυκείου Θέμα 1
viewtopic.php?f=58&t=32205 (Θέμα 2)
Α Λυκείου Θέμα 2
https://www.wiskundeolympiade.nl/files/ ... ven_en.pdf (Θέμα Β1)
Β Λυκείου Θέμα 2
Αφαιρώντας
 οπότε αντικαθιστώντας στην πρώτη
οπότε αντικαθιστώντας στην πρώτη  οπότε
οπότε 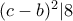 δηλ.
δηλ.  ή
ή 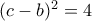 κτλ
κτλ Γ Λυκείου Θέμα 1
Είναι
 με ισότητα αν-ν
με ισότητα αν-ν  δηλαδή αν-ν
δηλαδή αν-ν 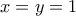 ή
ή 
Γ Λυκείου Θέμα 2
Γενικότερο: search.php?keywords=43&t=12692&sf=msgonly
Θανάσης Κοντογεώργης
Re: Συμπληρωματικός Θαλής 2020-2021
ΘΕΜΑ 3 - Γ ΛΥΚΕΙΟΥ
Έστω το σημείο τομής της
το σημείο τομής της  με τον
με τον  . Τότε
. Τότε 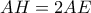 , αφού το
, αφού το  είναι ύψος, και άρα διάμεσος στο ισοσκελές τρίγωνο
είναι ύψος, και άρα διάμεσος στο ισοσκελές τρίγωνο 
Από την ομοιότητα των τριγώνων και
και  έπεται ότι
έπεται ότι

Αφού , από την παραπάνω σχέση έπεται ότι τα τρίγωνα
, από την παραπάνω σχέση έπεται ότι τα τρίγωνα  και
και  είναι όμοια.
είναι όμοια.
Έτσι,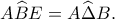
Έστω το συμμετρικό του
το συμμετρικό του  ως προς την διχοτόμο
ως προς την διχοτόμο  . Τότε το
. Τότε το  βρίσκεται πάνω στην
βρίσκεται πάνω στην  και είναι
και είναι

αφού στο ισοσκελές τρίγωνο έχουμε
έχουμε  .
.
Αφού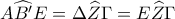 , το τετράπλευρο
, το τετράπλευρο  είναι εγγράψιμο.
είναι εγγράψιμο.
Συνεπώς, , λόγω συμμετρίας, όπως θέλαμε.
, λόγω συμμετρίας, όπως θέλαμε.
Έστω
 το σημείο τομής της
το σημείο τομής της  με τον
με τον  . Τότε
. Τότε 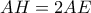 , αφού το
, αφού το  είναι ύψος, και άρα διάμεσος στο ισοσκελές τρίγωνο
είναι ύψος, και άρα διάμεσος στο ισοσκελές τρίγωνο 
Από την ομοιότητα των τριγώνων
 και
και  έπεται ότι
έπεται ότι
Αφού
 , από την παραπάνω σχέση έπεται ότι τα τρίγωνα
, από την παραπάνω σχέση έπεται ότι τα τρίγωνα  και
και  είναι όμοια.
είναι όμοια. Έτσι,
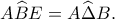
Έστω
 το συμμετρικό του
το συμμετρικό του  ως προς την διχοτόμο
ως προς την διχοτόμο  . Τότε το
. Τότε το  βρίσκεται πάνω στην
βρίσκεται πάνω στην  και είναι
και είναι
αφού στο ισοσκελές τρίγωνο
 έχουμε
έχουμε  .
.Αφού
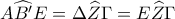 , το τετράπλευρο
, το τετράπλευρο  είναι εγγράψιμο.
είναι εγγράψιμο.Συνεπώς,
 , λόγω συμμετρίας, όπως θέλαμε.
, λόγω συμμετρίας, όπως θέλαμε.- Συνημμένα
-
- thales_2020_Γ3b.png (21.22 KiB) Προβλήθηκε 4060 φορές
Re: Συμπληρωματικός Θαλής 2020-2021
ΘΕΜΑ 3 - Β ΛΥΚΕΙΟΥ
(2ος τρόπος - με συνθετική γεωμετρία - Ο 1ος τρόπος με τριγωνομετρία είναι εδώ)
Έστω ότι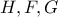 είναι τα σημεία τομής της
είναι τα σημεία τομής της  , της διχοτόμου της
, της διχοτόμου της 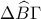 , και της
, και της  με τον περιγεγραμμένο κύκλο του τριγώνου
με τον περιγεγραμμένο κύκλο του τριγώνου  .
.
Έστω και
και 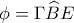 .
.
Στο ορθογώνιο τρίγωνο , η διάμεσος
, η διάμεσος 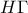 είναι ίση με το μισό της υποτείνουσας, οπότε
είναι ίση με το μισό της υποτείνουσας, οπότε  . Επιπλέον, αφού
. Επιπλέον, αφού 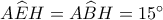 , έχουμε
, έχουμε  .
.
Αφού , έπεται ότι
, έπεται ότι  . Άρα το τρίγωνο
. Άρα το τρίγωνο  είναι ισοσκελές και η διχοτόμος
είναι ισοσκελές και η διχοτόμος  της
της  είναι μεσοκάθετος του
είναι μεσοκάθετος του 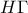 . Έτσι,
. Έτσι, 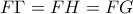 .
.
Τα τρίγωνα και
και  έχουν
έχουν 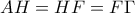 ,
,  και
και  , οπότε είναι ίσα (ΠΓΠ).
, οπότε είναι ίσα (ΠΓΠ).
Συνεπώς,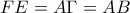 . Αφού ίσες χορδές αντιστοιχούν σε ίσα τόξα, έπεται ότι
. Αφού ίσες χορδές αντιστοιχούν σε ίσα τόξα, έπεται ότι
 . Αλλά,
. Αλλά, 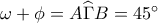 . Συνεπώς,
. Συνεπώς,
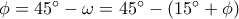 , απ' όπου έπεται άμεσα ότι
, απ' όπου έπεται άμεσα ότι 
(2ος τρόπος - με συνθετική γεωμετρία - Ο 1ος τρόπος με τριγωνομετρία είναι εδώ)
Έστω ότι
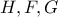 είναι τα σημεία τομής της
είναι τα σημεία τομής της  , της διχοτόμου της
, της διχοτόμου της 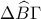 , και της
, και της  με τον περιγεγραμμένο κύκλο του τριγώνου
με τον περιγεγραμμένο κύκλο του τριγώνου  .
.Έστω
 και
και 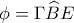 .
. Στο ορθογώνιο τρίγωνο
 , η διάμεσος
, η διάμεσος 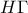 είναι ίση με το μισό της υποτείνουσας, οπότε
είναι ίση με το μισό της υποτείνουσας, οπότε  . Επιπλέον, αφού
. Επιπλέον, αφού 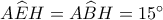 , έχουμε
, έχουμε  .
. Αφού
 , έπεται ότι
, έπεται ότι  . Άρα το τρίγωνο
. Άρα το τρίγωνο  είναι ισοσκελές και η διχοτόμος
είναι ισοσκελές και η διχοτόμος  της
της  είναι μεσοκάθετος του
είναι μεσοκάθετος του 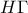 . Έτσι,
. Έτσι, 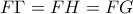 .
.Τα τρίγωνα
 και
και  έχουν
έχουν 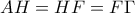 ,
,  και
και  , οπότε είναι ίσα (ΠΓΠ).
, οπότε είναι ίσα (ΠΓΠ).Συνεπώς,
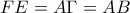 . Αφού ίσες χορδές αντιστοιχούν σε ίσα τόξα, έπεται ότι
. Αφού ίσες χορδές αντιστοιχούν σε ίσα τόξα, έπεται ότι . Αλλά,
. Αλλά, 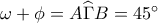 . Συνεπώς,
. Συνεπώς,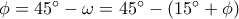 , απ' όπου έπεται άμεσα ότι
, απ' όπου έπεται άμεσα ότι 
- Συνημμένα
-
- thales_2020b_B2b.png (17.66 KiB) Προβλήθηκε 3999 φορές
Re: Συμπληρωματικός Θαλής 2020-2021
Ωραία λύση Αχιλλέα!
Έχω υπόψη μου άλλες δύο συνθετικές λύσεις. Θα δώσω hint για την πιο απρόσμενη (κατά την άποψή μου). Μπορούμε να χρησιμοποιήσουμε τη γνωστή άσκηση viewtopic.php?f=20&t=16341&p=84868&hili ... %BF#p84868
για να καταλήξουμε στο συμπέρασμα!
Σιλουανός Μπραζιτίκος
- Γιώργος Μήτσιος
- Δημοσιεύσεις: 1789
- Εγγραφή: Κυρ Ιούλ 01, 2012 10:14 am
- Τοποθεσία: Aρτα
Re: Συμπληρωματικός Θαλής 2020-2021
Καλησπέρα! Για το θέμα 3 της Β΄Λυκείου.
Με τα εργαλεία της Ευκλείδειας και χρήση του σχήματος Έστω και
και  . Τότε
. Τότε 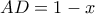 ενώ
ενώ  .
.
Το Πυθαγόρειο στο τρίγωνο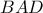 δίνει
δίνει 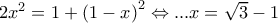
και στο έχουμε
έχουμε  , άρα
, άρα  οπότε
οπότε 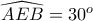 και τέλος
και τέλος  .
.
Φιλικά, Γιώργος.
Με τα εργαλεία της Ευκλείδειας και χρήση του σχήματος Έστω
 και
και  . Τότε
. Τότε 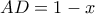 ενώ
ενώ  .
.Το Πυθαγόρειο στο τρίγωνο
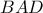 δίνει
δίνει 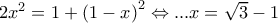
και στο
 έχουμε
έχουμε  , άρα
, άρα  οπότε
οπότε 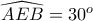 και τέλος
και τέλος  .
.Φιλικά, Γιώργος.
Re: Συμπληρωματικός Θαλής 2020-2021
Μια λύση με την υπόδειξη του Σιλουανού.silouan έγραψε: ↑Σάβ Μάιος 15, 2021 3:40 pmΩραία λύση Αχιλλέα!
Έχω υπόψη μου άλλες δύο συνθετικές λύσεις. Θα δώσω hint για την πιο απρόσμενη (κατά την άποψή μου). Μπορούμε να χρησιμοποιήσουμε τη γνωστή άσκηση viewtopic.php?f=20&t=16341&p=84868&hili ... %BF#p84868
για να καταλήξουμε στο συμπέρασμα!
Θεωρούμε το τετράγωνο
 , όπου
, όπου  είναι το συμμετρικό του
είναι το συμμετρικό του  ως προς το
ως προς το  , το οποίο έχει κέντρο το σημείο
, το οποίο έχει κέντρο το σημείο  αφού
αφού 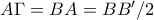 . Το συμμετρικό
. Το συμμετρικό  του
του  ως προς το
ως προς το  ανήκει στην
ανήκει στην 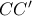 και αφού
και αφού  , είναι
, είναι  . Εύκολα βλέπουμε ότι τα ορθογώνια τρίγωνα
. Εύκολα βλέπουμε ότι τα ορθογώνια τρίγωνα  και
και  είναι ίσα, και έτσι
είναι ίσα, και έτσι  και
και 
Από το πρόβλημα της υπόδειξης του Σιλουανού, το τρίγωνο
 είναι ισόπλευρο, οπότε
είναι ισόπλευρο, οπότε  .
.Φιλικά,
Αχιλλέας
- Συνημμένα
-
- thales_2020c_B3b.png (15.34 KiB) Προβλήθηκε 3805 φορές
Re: Συμπληρωματικός Θαλής 2020-2021
ΘΕΜΑ 3 - Α ΛΥΚΕΙΟΥ
Παρατηρούμε ότι η διάμεσος είναι διχοτόμος της
είναι διχοτόμος της  και ύψος στο ισοσκελές τρίγωνο
και ύψος στο ισοσκελές τρίγωνο  . Άρα το
. Άρα το  είναι το έγκεντρο του τριγώνου
είναι το έγκεντρο του τριγώνου  και ισαπέχει από τiς πλευρές της γωνίας
και ισαπέχει από τiς πλευρές της γωνίας 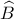 . Έτσι,
. Έτσι,  .
.
Έστω το συμμετρικό του
το συμμετρικό του  ως προς το
ως προς το  . Τότε το
. Τότε το  είναι παραλληλόγραμμο, αφού οι διαγώνιοι του διχοτομούνται. Συνεπώς η
είναι παραλληλόγραμμο, αφού οι διαγώνιοι του διχοτομούνται. Συνεπώς η 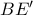 είναι παράλληλη στη
είναι παράλληλη στη 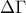 .
.
Αφού , το
, το 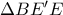 είναι ισοσκελές τράπέζιο, οπότε
είναι ισοσκελές τράπέζιο, οπότε
 .
.
Παρατηρούμε ότι η διάμεσος
 είναι διχοτόμος της
είναι διχοτόμος της  και ύψος στο ισοσκελές τρίγωνο
και ύψος στο ισοσκελές τρίγωνο  . Άρα το
. Άρα το  είναι το έγκεντρο του τριγώνου
είναι το έγκεντρο του τριγώνου  και ισαπέχει από τiς πλευρές της γωνίας
και ισαπέχει από τiς πλευρές της γωνίας 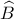 . Έτσι,
. Έτσι,  .
. Έστω
 το συμμετρικό του
το συμμετρικό του  ως προς το
ως προς το  . Τότε το
. Τότε το  είναι παραλληλόγραμμο, αφού οι διαγώνιοι του διχοτομούνται. Συνεπώς η
είναι παραλληλόγραμμο, αφού οι διαγώνιοι του διχοτομούνται. Συνεπώς η 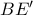 είναι παράλληλη στη
είναι παράλληλη στη 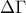 .
.Αφού
 , το
, το 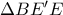 είναι ισοσκελές τράπέζιο, οπότε
είναι ισοσκελές τράπέζιο, οπότε .
.- Συνημμένα
-
- thales_2020_A3b.png (13.22 KiB) Προβλήθηκε 3761 φορές
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης

 , όπου όλοι οι παράγοντες είναι πρώτοι αριθμοί.
, όπου όλοι οι παράγοντες είναι πρώτοι αριθμοί.