Πανρωσική Μαθηματική Ολυμπιάδα 2021 (11η τάξη, 2η μέρα)

[Al.Koutsouridis]

Πανρωσική Μαθητική Μαθηματική Ολυμπιάδα 2021.
2η μέρα: Θέματα της 4ης φάσης (τελικής) για την 11η τάξη.


1. Δίνεται ένα άπειρο τετραγωνισμένο επίπεδο. Η δασκάλα και η τάξη που αποτελείται από μαθητές παίζουν ένα παιχνίδι. Κάνουν κινήσεις με την σειρά, στην αρχή η δασκάλα, ύστερα με την σειρά όλοι οι μαθητές, ύστερα πάλι η δασκάλα κ.ο.κ. Με μια κίνηση επιτρέπεται να χρωματιστεί μοναδιαίο τμήμα, που αποτελεί το σύνορο δυο γειτονικών κελιών. Δεν επιτρέπεται να χρωματιστεί ένα τμήμα δυο φορές. Η δασκάλα κερδίζει, αν μετά από κίνηση ενός εκ των παικτών βρεθεί ένα τετραγωνισμένο ορθογώνιο ή , τέτοιο ώστε όλη η περίμετρός του να είναι χρωματισμένη, αλλά το μοναδιαίο τμήμα στο εσωτερικό του όχι. Μπορούν οι μαθητές να αποτρέψουν την δασκάλα να κερδίσει; (Μ.Ντίντιν, Α.Κουζνέτσοβ)


2. Στο τετράεδρο τα μήκη όλων των ακμών του είναι διαφορετικά. Το σημείο του επιπέδου είναι το συμμετρικό του ως προς την μεσοκάθετη του τμήματος . Το σημείο του επιπέδου και το σημείο του επιπέδου 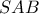ορίζονται ανάλογα. να αποδείξετε, ότι τα επίπεδα , , και έχουν κοινό σημείο. (Α.Κουζνέτσοβ)


3. Να βρείτε όλες τις μεταθέσεις των αριθμών τέτοιες, ώστε για οποιουσδήποτε δυο θετικούς ακέραιους , που ικανοποιούν την συνθήκη , να αληθεύει η ανίσωση: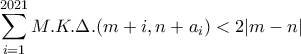

.

(Μετάθεση είναι μια ακολουθία, στην οποία καθένας εκ των αριθμών εμφανίζεται ακριβώς μία φορά.) (Π.Κοζλόβ)


4. Καθένα από κορίτσια έχει από βόλους. Μεταξύ αυτών των βόλων υπάρχουν από βόλοι διαφορετικών χρωμάτων. Δυο κορίτσια μπορούν να ανταλλάξουν βόλους, δίνοντας η μια στην άλλη από ένα βόλο. Θέλουν να επιτύχουν κάθε κορίτσι να έχει βόλους διαφορετικών χρωμάτων. Να αποδείξετε, ότι μπορούν να το πετύχουν αυτό με τέτοια ακολουθία ανταλλαγών, ώστε κάθε βόλος να συμμετέχει το πολύ σε μια ανταλλαγή. (Ι.Μπογκτάνοβ, Θ.Πετρόβ)