 , τέτοιοι ώστε
, τέτοιοι ώστε  . Να αποδείξετε ότι:
. Να αποδείξετε ότι:
Πρόβλημα 2: Να βρείτε όλα τα ζεύγη φυσικών αριθμών
 για τα οποίων αν
για τα οποίων αν  ο μέγιστος κοινός διαιρέτης των
ο μέγιστος κοινός διαιρέτης των  και
και  το ελάχιστο κοινό πολλαπλάσιό των
το ελάχιστο κοινό πολλαπλάσιό των  , τότε
, τότε 
Πρόβλημα 3: Δίνεται ρόμβος
 .
.(α) Να αποδείξετε ότι μπορείτε να κατασκευάσετε ένα κύκλο
 που να είναι εγγεγραμμένος στον ρόμβο και να εφάπτεται των πλευρών του.
που να είναι εγγεγραμμένος στον ρόμβο και να εφάπτεται των πλευρών του.(β) Τα σημεία
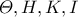 βρίσκονται πάνω στις πλευρές
βρίσκονται πάνω στις πλευρές  του ρόμβου αντίστοιχα, έτσι ώστε τα ευθύγραμμα τμήματα
του ρόμβου αντίστοιχα, έτσι ώστε τα ευθύγραμμα τμήματα  και
και  να είναι εφαπτόμενα στον κύκλο
να είναι εφαπτόμενα στον κύκλο  . Να αποδείξετε ότι το τετράπλευρο που ορίζεται από τα σημεία
. Να αποδείξετε ότι το τετράπλευρο που ορίζεται από τα σημεία 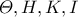 είναι τραπέζιο.
είναι τραπέζιο.Πρόβλημα 4: Χρωματίζουμε κάθε τετραγωνάκι μιας
 σκακιέρας με ένα από τα χρώματα κόκκινο, πράσινο και μπλε. Να αποδείξετε πως όπως και να γίνει αυτός ο χρωματισμός, μπορούμε να βρούμε δυο οριζόντιες σειρές και δυο κάθετες στήλες, ώστε τα
σκακιέρας με ένα από τα χρώματα κόκκινο, πράσινο και μπλε. Να αποδείξετε πως όπως και να γίνει αυτός ο χρωματισμός, μπορούμε να βρούμε δυο οριζόντιες σειρές και δυο κάθετες στήλες, ώστε τα  τετραγωνάκια που βρίσκονται στις τομές αυτών των γραμμών να έχουν όλα το ίδιο χρώμα.
τετραγωνάκια που βρίσκονται στις τομές αυτών των γραμμών να έχουν όλα το ίδιο χρώμα.
![\displaystyle{xyz(x+y+z)+2021=x^2yz+xy^2z+xyz^2+\underbrace{1+1+\cdots +1}_{2021 ~terms}\geq 2024\sqrt[2024]{(xyz)^4}.} \displaystyle{xyz(x+y+z)+2021=x^2yz+xy^2z+xyz^2+\underbrace{1+1+\cdots +1}_{2021 ~terms}\geq 2024\sqrt[2024]{(xyz)^4}.}](/forum/ext/geomar/texintegr/latexrender/pictures/030f655f54d828924edfb2588e28feeb.png)
![\displaystyle{\sqrt[2024]{(xyz)^4} \geq xyz,} \displaystyle{\sqrt[2024]{(xyz)^4} \geq xyz,}](/forum/ext/geomar/texintegr/latexrender/pictures/51b926ef279730f38585c13c0ec5bb17.png) δηλαδή
δηλαδή  Αυτό είναι συνέπεια της
Αυτό είναι συνέπεια της ![\displaystyle{x^2+y^2+z^2\geq 3\sqrt[3]{(xyz)^2}} \displaystyle{x^2+y^2+z^2\geq 3\sqrt[3]{(xyz)^2}}](/forum/ext/geomar/texintegr/latexrender/pictures/beaca3f30d39ed16f4c040c2b3d053c9.png) .
.![\dfrac{x^{2}+y^{2}+z^{2}}{3}=1\geq \sqrt[3]{(xyz)^{2}}\Leftrightarrow xyz \leq 1 \dfrac{x^{2}+y^{2}+z^{2}}{3}=1\geq \sqrt[3]{(xyz)^{2}}\Leftrightarrow xyz \leq 1](/forum/ext/geomar/texintegr/latexrender/pictures/36e13ccafb4389bd256e661b4f7cc519.png)


 που ισχύει από AM-GM
που ισχύει από AM-GM τον Μ.Κ.Δ. και
τον Μ.Κ.Δ. και  το Ε.Κ.Π.
το Ε.Κ.Π.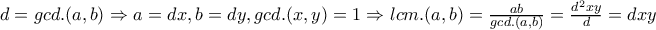 .
.![d+dxy=4dx+4dy+2021 \Rightarrow d[(xy-4x)+(-4y+16)+1-16]=2021 \Rightarrow d+dxy=4dx+4dy+2021 \Rightarrow d[(xy-4x)+(-4y+16)+1-16]=2021 \Rightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/3040fa13aa0ccd3a039a1ab2eaabc9d7.png)
![\Rightarrow d[x(y-4)-4(y-4)-15]=2021 \Rightarrow d[(x-4)(y-4)-15]=2021 \Rightarrow d|2021=43 \cdot 47 \Rightarrow \Rightarrow d[x(y-4)-4(y-4)-15]=2021 \Rightarrow d[(x-4)(y-4)-15]=2021 \Rightarrow d|2021=43 \cdot 47 \Rightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/492707211e3415e9cd4398330892d871.png)
 .
.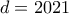 .
. .
. τότε
τότε  , άτοπο.
, άτοπο. , τότε
, τότε  , άτοπο.
, άτοπο. ,τότε
,τότε  , άτοπο.
, άτοπο. απορρίπτονται και οι υπόλοιπες περιπτώσεις.
απορρίπτονται και οι υπόλοιπες περιπτώσεις. .
. .
.
 και η μετάθεσή της
και η μετάθεσή της  .
. , άτοπο.
, άτοπο. .
. .
.
 και η μετάθεσή της
και η μετάθεσή της  .
.
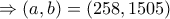 , και η μετάθεσή της
, και η μετάθεσή της  .
. .
.
 .
. , άτοπο.
, άτοπο. , άτοπο.
, άτοπο.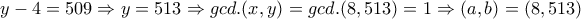 ,
, .
. και οι μεταθέσεις τους.
και οι μεταθέσεις τους. φορές (
φορές ( )
) υπάρχουν
υπάρχουν  τρόποι για να υπερτερεί ένα χρώμα.
τρόποι για να υπερτερεί ένα χρώμα. .
. και κάθε τετραγώνω βάφεται μαύρο η άσπρο να αποδειχθεί ότι μπορούμε να βρούμε δυο οριζόντιες σειρές και δυο κάθετες στήλες, ώστε τα
και κάθε τετραγώνω βάφεται μαύρο η άσπρο να αποδειχθεί ότι μπορούμε να βρούμε δυο οριζόντιες σειρές και δυο κάθετες στήλες, ώστε τα  αλλά στην Αμερική είχαν δώσει
αλλά στην Αμερική είχαν δώσει  σκακιέρας με ένα από τα
σκακιέρας με ένα από τα  χρώματα . Να αποδείξετε πως όπως και να γίνει αυτός ο χρωματισμός, μπορούμε να βρούμε δυο οριζόντιες σειρές και δυο κάθετες στήλες, ώστε τα
χρώματα . Να αποδείξετε πως όπως και να γίνει αυτός ο χρωματισμός, μπορούμε να βρούμε δυο οριζόντιες σειρές και δυο κάθετες στήλες, ώστε τα  στήλες τότε μπορεί να μην υπάρχει ορθογώνιο με γωνίες του ιδίου χρώματος.
στήλες τότε μπορεί να μην υπάρχει ορθογώνιο με γωνίες του ιδίου χρώματος. τα
τα 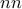 χρώματα βάφουμε με τόν εξής τρόπο:
χρώματα βάφουμε με τόν εξής τρόπο: έως
έως  να υπάρχουν ακριβώς 2 τετράγωνα με το χρώμα
να υπάρχουν ακριβώς 2 τετράγωνα με το χρώμα έτσι έστω να υπάρχουν όλοι οι τρόποι που μπορώ να χρωματισω
έτσι έστω να υπάρχουν όλοι οι τρόποι που μπορώ να χρωματισω  τετράγωνα με μια στήλη (αυτό γίνεται με
τετράγωνα με μια στήλη (αυτό γίνεται με  τρόπους άρα όλοι είναι διαφορετική) και τα άλλα
τρόπους άρα όλοι είναι διαφορετική) και τα άλλα  τετραγονα κάθε στήλης τα βάφουμε εστί ώστε να περιέχουν ακριβώς μία φορά κάθε χρώμα (διαφορετικό του
τετραγονα κάθε στήλης τα βάφουμε εστί ώστε να περιέχουν ακριβώς μία φορά κάθε χρώμα (διαφορετικό του  είναι το ελάχιστο.
είναι το ελάχιστο. με
με 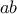 ελάχιστο.
ελάχιστο.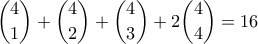
 εμφανίζεται
εμφανίζεται  , τότε θα υπάρχουν
, τότε θα υπάρχουν  τουλάχιστον τρόποι που θα εμφανίζονται
τουλάχιστον τρόποι που θα εμφανίζονται  θα είναι ίσα, και ο κύκλος με ακτίνα το ύψος θα είναι εγγεγραμμένος και θα εφάπτεται των πλευρών του ρόμβου
θα είναι ίσα, και ο κύκλος με ακτίνα το ύψος θα είναι εγγεγραμμένος και θα εφάπτεται των πλευρών του ρόμβου