 για τα οποία ισχύει η εξίσωση
για τα οποία ισχύει η εξίσωση 
Πρόβλημα 2: Δίνονται οι θετικοί πραγματικοί πραγματικοί αριθμοί
 τέτοιοι ώστε
τέτοιοι ώστε  και
και  . Αν
. Αν  είναι οι αριθμοί
είναι οι αριθμοί 
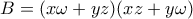
να βρείτε την ελάχιστη δυνατή τιμή της διαφοράς
 .
.Πρόβλημα 3: Δίνεται παραλληλόγραμμο
 και έστω
και έστω  το σημείο τομής των διαγωνίων του. Οι παράλληλες ευθείες από τα σημεία
το σημείο τομής των διαγωνίων του. Οι παράλληλες ευθείες από τα σημεία  και
και  προς τις
προς τις  και
και  αντίστοιχα τέμνονται στο σημείο
αντίστοιχα τέμνονται στο σημείο  . Η ευθεία
. Η ευθεία  τέμνει τις
τέμνει τις  και
και  στα σημεία
στα σημεία  και
και  αντίστοιχα. Αν
αντίστοιχα. Αν  το σημείο τομής των ευθειών
το σημείο τομής των ευθειών  και
και  να αποδείξετε:
να αποδείξετε:(α) Η ευθεία
 περνά από το μέσο του
περνά από το μέσο του 
(β)

Πρόβλημα 4: Δύο παιδιά, ο Νικόλας και ο Γιώργος παίζουν μερικές φορές ένα παιχνίδι στο οποίο ο νικητής συγκεντρώνει
 πόντους και ο χαμένος
πόντους και ο χαμένος  πόντους, όπου
πόντους, όπου  είναι μη αρνητικοί ακέραιοι αριθμοί με
είναι μη αρνητικοί ακέραιοι αριθμοί με 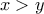 . Υποθέτουμε ότι σε κάθε παιχνίδι ένα από τα παιδιά είναι ο νικητής και ο άλλος ο χαμένος.
. Υποθέτουμε ότι σε κάθε παιχνίδι ένα από τα παιδιά είναι ο νικητής και ο άλλος ο χαμένος. Αφού έπαιξαν ορισμένα παιχνίδια, ο Νικόλας συγκέντρωσε συνολικά
 πόντους και ο Γιώργος συγκέντρωσε συνολικά
πόντους και ο Γιώργος συγκέντρωσε συνολικά  πόντους. Αν ξέρουμε ότι ο Γιώργος κέρδισε
πόντους. Αν ξέρουμε ότι ο Γιώργος κέρδισε  παιχνίδια, να βρείτε τα
παιχνίδια, να βρείτε τα  και
και  .
.
 διάφορη του 2 τότε άρτιος=περιττός.
διάφορη του 2 τότε άρτιος=περιττός. η
η :
: που σημαίνει
που σημαίνει τα
τα  δέχτη
δέχτη που σημαίνει
που σημαίνει  που δεν είναι δέχτη
που δεν είναι δέχτη
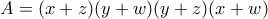


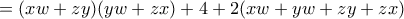
![=B+4+2(xw+yw+zy+zx)\geq B+4+8\sqrt[4]{(xyzw)^2} =B+4+2(xw+yw+zy+zx)\geq B+4+8\sqrt[4]{(xyzw)^2}](/forum/ext/geomar/texintegr/latexrender/pictures/ca89e35a698ce15a1928b8399e0a3dda.png)
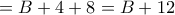

 το πλήθος των νικών του Νικόλα τότε:
το πλήθος των νικών του Νικόλα τότε: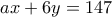
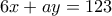



 αλλιώς θα πρέπει
αλλιώς θα πρέπει 
 .
.
 είναι όντως εφικτή με
είναι όντως εφικτή με  .Άρα η ελάχιστη τιμή είναι το 12
.Άρα η ελάχιστη τιμή είναι το 12 και
και  , καθιστούν το
, καθιστούν το  .
.