ΙΜΟ 2020
Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3342
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
ΙΜΟ 2020
Τι γίνεται; Άλλαξε κάτι στο  ; Εντάξει, λόγω κορονοϊού και εξ αποστάσεως εξέτασης δεν ανέμενα να δω τα θέματα της φετεινής ΙΜΟ χθες και προχθές, αλλά σήμερα ... γιατί όχι; Τα ανεβάζω λοιπόν, από τον επίσημο ιστότοπο της ΙΜΟ 2020 (στα Ελληνικά), στο συνημμένο χωρίς σχόλια, δεν είμαι άλλωστε και ο πιο κατάλληλος εδώ μέσα γι αυτό, απλώς ας τα απολαύσουμε (όλοι) χωρίς να τα λύσουμε (οι περισσότεροι)
; Εντάξει, λόγω κορονοϊού και εξ αποστάσεως εξέτασης δεν ανέμενα να δω τα θέματα της φετεινής ΙΜΟ χθες και προχθές, αλλά σήμερα ... γιατί όχι; Τα ανεβάζω λοιπόν, από τον επίσημο ιστότοπο της ΙΜΟ 2020 (στα Ελληνικά), στο συνημμένο χωρίς σχόλια, δεν είμαι άλλωστε και ο πιο κατάλληλος εδώ μέσα γι αυτό, απλώς ας τα απολαύσουμε (όλοι) χωρίς να τα λύσουμε (οι περισσότεροι) 
Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Λέξεις Κλειδιά:
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: ΙΜΟ 2020
Η αλήθεια είναι ότι είχα δει τα προβλήματα αλλά δεν ήμουν σίγουρος από πότε μπορούμε να τα μοιραστούμε λόγω των φετινών ιδιαιτεροτήτων. Αφού όμως ανέβηκαν στην επίσημη ιστοσελίδα τότε είμαστε εντάξει.
Θα περιμένω λίγο πριν ανεβάσω τις λύσεις μου σε κάποια εξ αυτών.
Θα περιμένω λίγο πριν ανεβάσω τις λύσεις μου σε κάποια εξ αυτών.
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: ΙΜΟ 2020
Βάζω τη λύση μου για το 3.
Χωρίζουμε τα βότσαλα στα ακόλουθα ζεύγη:
ζεύγη:  . Επειδή σε κάθε ζεύγος έχουμε το ίδιο συνολικό βάρος, αρκεί να δείξουμε ότι μπορούμε να χωρίσουμε αυτά τα
. Επειδή σε κάθε ζεύγος έχουμε το ίδιο συνολικό βάρος, αρκεί να δείξουμε ότι μπορούμε να χωρίσουμε αυτά τα  ζεύγη σε
ζεύγη σε  ομάδες των
ομάδες των  ζευγών ώστε σε κάθε ομάδα να έχουμε από δύο βότσαλα κάθε χρώματος.
ζευγών ώστε σε κάθε ομάδα να έχουμε από δύο βότσαλα κάθε χρώματος.
Κατασκευάζουμε τώρα ένα γράφημα με κορυφές τα χρώματα, όπου συνδέουμε δύο χρώματα αν και μόνο κάποια από τα πιο πάνω ζεύγη έχει ένα βότσαλο με το ένα χρώμα και ένα βότσαλο με το άλλο. Στο γράφημά μας επιτρέπουμε ακμές με πολλαπλότητα (βάζουμε τόσες ακμές όσα και τα ζεύγη των συγκεκριμένων χρωμάτων) και βρόχους (δηλαδή ακμές από μία κορυφή στην ίδια).
Στο γράφημά μας κάθε κορυφή έχει βαθμό . (Κάθε βρόχος δίνει βαθμό
. (Κάθε βρόχος δίνει βαθμό  στην κορυφή.) Αυτό που ψάχνουμε είναι ένα υπογράφημα όπου κάθε κορυφή έχει βαθμό
στην κορυφή.) Αυτό που ψάχνουμε είναι ένα υπογράφημα όπου κάθε κορυφή έχει βαθμό  . Αυτό είναι συνέπεια ενός θεωρήματος του Petersen που λέει ότι κάθε κανονικό γράφημα βαθμού
. Αυτό είναι συνέπεια ενός θεωρήματος του Petersen που λέει ότι κάθε κανονικό γράφημα βαθμού  έχει κανονικό υπογράφημα βαθμού
έχει κανονικό υπογράφημα βαθμού  .
.
Στην περίπτωσή μας ( ) η απόδειξη δεν είναι δύσκολη. Χρησιμοποιούμε το θεώρημα για την ύπαρξη κύκλων Euler και ... σχεδόν τελειώσαμε. Αφήνω να το σκεφτείτε πως. Για
) η απόδειξη δεν είναι δύσκολη. Χρησιμοποιούμε το θεώρημα για την ύπαρξη κύκλων Euler και ... σχεδόν τελειώσαμε. Αφήνω να το σκεφτείτε πως. Για  η απόδειξη πάλι δεν είναι δύσκολη αλλά θέλει ακόμη κάτι επιπλέον.
η απόδειξη πάλι δεν είναι δύσκολη αλλά θέλει ακόμη κάτι επιπλέον.
Χωρίζουμε τα βότσαλα στα ακόλουθα
 ζεύγη:
ζεύγη:  . Επειδή σε κάθε ζεύγος έχουμε το ίδιο συνολικό βάρος, αρκεί να δείξουμε ότι μπορούμε να χωρίσουμε αυτά τα
. Επειδή σε κάθε ζεύγος έχουμε το ίδιο συνολικό βάρος, αρκεί να δείξουμε ότι μπορούμε να χωρίσουμε αυτά τα  ζεύγη σε
ζεύγη σε  ομάδες των
ομάδες των  ζευγών ώστε σε κάθε ομάδα να έχουμε από δύο βότσαλα κάθε χρώματος.
ζευγών ώστε σε κάθε ομάδα να έχουμε από δύο βότσαλα κάθε χρώματος.Κατασκευάζουμε τώρα ένα γράφημα με κορυφές τα χρώματα, όπου συνδέουμε δύο χρώματα αν και μόνο κάποια από τα πιο πάνω ζεύγη έχει ένα βότσαλο με το ένα χρώμα και ένα βότσαλο με το άλλο. Στο γράφημά μας επιτρέπουμε ακμές με πολλαπλότητα (βάζουμε τόσες ακμές όσα και τα ζεύγη των συγκεκριμένων χρωμάτων) και βρόχους (δηλαδή ακμές από μία κορυφή στην ίδια).
Στο γράφημά μας κάθε κορυφή έχει βαθμό
 . (Κάθε βρόχος δίνει βαθμό
. (Κάθε βρόχος δίνει βαθμό  στην κορυφή.) Αυτό που ψάχνουμε είναι ένα υπογράφημα όπου κάθε κορυφή έχει βαθμό
στην κορυφή.) Αυτό που ψάχνουμε είναι ένα υπογράφημα όπου κάθε κορυφή έχει βαθμό  . Αυτό είναι συνέπεια ενός θεωρήματος του Petersen που λέει ότι κάθε κανονικό γράφημα βαθμού
. Αυτό είναι συνέπεια ενός θεωρήματος του Petersen που λέει ότι κάθε κανονικό γράφημα βαθμού  έχει κανονικό υπογράφημα βαθμού
έχει κανονικό υπογράφημα βαθμού  .
. Στην περίπτωσή μας (
 ) η απόδειξη δεν είναι δύσκολη. Χρησιμοποιούμε το θεώρημα για την ύπαρξη κύκλων Euler και ... σχεδόν τελειώσαμε. Αφήνω να το σκεφτείτε πως. Για
) η απόδειξη δεν είναι δύσκολη. Χρησιμοποιούμε το θεώρημα για την ύπαρξη κύκλων Euler και ... σχεδόν τελειώσαμε. Αφήνω να το σκεφτείτε πως. Για  η απόδειξη πάλι δεν είναι δύσκολη αλλά θέλει ακόμη κάτι επιπλέον.
η απόδειξη πάλι δεν είναι δύσκολη αλλά θέλει ακόμη κάτι επιπλέον.- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: ΙΜΟ 2020
Ας δούμε και μια λύση για το 2.
Παρατηρώ αρχικά ότι

Επίσης ισχύει ότι .
.
Άρα έχουμε
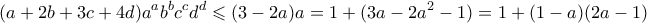
Από εδώ προκύπτει το ζητούμενη στην περίπτωση όπου . Μπορώ λοιπόν να υποθέσω ότι
. Μπορώ λοιπόν να υποθέσω ότι  .
.
Τότε με παρόμοιο τρόπο όπως πιο πάνω παίρνω

Έστω . Αρκεί να δείξω ότι
. Αρκεί να δείξω ότι  για
για ![x \in [1/2,1] x \in [1/2,1]](/forum/ext/geomar/texintegr/latexrender/pictures/0037e81b6b973c459760d8462e65bffe.png) .
.
Ορίζω και παρατηρώ ότι
και παρατηρώ ότι

Όμως
Άρα η είναι κυρτή συνάρτηση και επομένως μεγιστοποιείται στα άκρα. Το ίδιο συμβαίνει και για την
είναι κυρτή συνάρτηση και επομένως μεγιστοποιείται στα άκρα. Το ίδιο συμβαίνει και για την  . Όμως
. Όμως  άρα όντως
άρα όντως  για κάθε
για κάθε ![x \in [1/2,1] x \in [1/2,1]](/forum/ext/geomar/texintegr/latexrender/pictures/0037e81b6b973c459760d8462e65bffe.png) όπως θέλαμε να δείξουμε.
όπως θέλαμε να δείξουμε.
Παρατηρώ αρχικά ότι

Επίσης ισχύει ότι
 .
.Άρα έχουμε
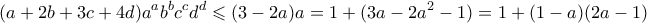
Από εδώ προκύπτει το ζητούμενη στην περίπτωση όπου
 . Μπορώ λοιπόν να υποθέσω ότι
. Μπορώ λοιπόν να υποθέσω ότι  .
. Τότε με παρόμοιο τρόπο όπως πιο πάνω παίρνω

Έστω
 . Αρκεί να δείξω ότι
. Αρκεί να δείξω ότι  για
για ![x \in [1/2,1] x \in [1/2,1]](/forum/ext/geomar/texintegr/latexrender/pictures/0037e81b6b973c459760d8462e65bffe.png) .
.Ορίζω
 και παρατηρώ ότι
και παρατηρώ ότι
Όμως

Άρα η
 είναι κυρτή συνάρτηση και επομένως μεγιστοποιείται στα άκρα. Το ίδιο συμβαίνει και για την
είναι κυρτή συνάρτηση και επομένως μεγιστοποιείται στα άκρα. Το ίδιο συμβαίνει και για την  . Όμως
. Όμως  άρα όντως
άρα όντως  για κάθε
για κάθε ![x \in [1/2,1] x \in [1/2,1]](/forum/ext/geomar/texintegr/latexrender/pictures/0037e81b6b973c459760d8462e65bffe.png) όπως θέλαμε να δείξουμε.
όπως θέλαμε να δείξουμε.Re: ΙΜΟ 2020
Μια άλλη προσέγγιση στο πρόβλημα 2 είναι η εξής:

Η δεύτερη στη σειρά ανισότητα προκύπτει από την βαρών και η πρώτη προκύπτει με πράξεις.
Η σκέψη βέβαια είναι ανάποδη. Πρώτα κάνω βαρών και μετά (από αρκετό ψάξιμο), ομογενοποίηση και πράξεις.

Η δεύτερη στη σειρά ανισότητα προκύπτει από την βαρών και η πρώτη προκύπτει με πράξεις.
Η σκέψη βέβαια είναι ανάποδη. Πρώτα κάνω βαρών και μετά (από αρκετό ψάξιμο), ομογενοποίηση και πράξεις.
Re: ΙΜΟ 2020
Μία λύση για το Πρόβλημα 1:
Έστω το κέντρο του περιγεγραμμένου κύκλου του τριγώνου
το κέντρο του περιγεγραμμένου κύκλου του τριγώνου . Θα αποδείξουμε ότι είναι το ζητούμενο σημείο τομής των δεδομένων ευθειών. Έστω
. Θα αποδείξουμε ότι είναι το ζητούμενο σημείο τομής των δεδομένων ευθειών. Έστω  και
και  . Από την υπόθεση θα ισχύει:
. Από την υπόθεση θα ισχύει: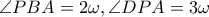 και
και  . Επιπλέον, θα ισχύει
. Επιπλέον, θα ισχύει (ως επίκεντρη που βαίνει στο ίδιο τόξο με την εγγεγραμμένη
(ως επίκεντρη που βαίνει στο ίδιο τόξο με την εγγεγραμμένη ) και
) και (ως επίκεντρη που βαίνει στο ίδιο τόξο με την εγγεγραμμένη
(ως επίκεντρη που βαίνει στο ίδιο τόξο με την εγγεγραμμένη  ). Στο τρίγωνο
). Στο τρίγωνο  :
:
 . Επίσης, στο τρίγωνο
. Επίσης, στο τρίγωνο :
:  . Στο τετράπλευρο
. Στο τετράπλευρο  οι απέναντι γωνίες
οι απέναντι γωνίες και
και 
είναι παραπληρωματικές, εφόσον . Επομένως είναι εγγράψιμο. Στο τετράπλευρο
. Επομένως είναι εγγράψιμο. Στο τετράπλευρο  , οι απέναντι γωνίες
, οι απέναντι γωνίες  και
και  είναι παραπληρωματικές, εφόσον
είναι παραπληρωματικές, εφόσον  . Eπομένως είναι εγγράψιμο. Παρατηρούμε ότι
. Eπομένως είναι εγγράψιμο. Παρατηρούμε ότι  (ως ακτίνες του περίκυκλου του τριγώνου
(ως ακτίνες του περίκυκλου του τριγώνου ), άρα το τρίγωνο
), άρα το τρίγωνο είναι ισοσκελές, άρα
είναι ισοσκελές, άρα  . Από το εγγράψιμο τετράπλευρο
. Από το εγγράψιμο τετράπλευρο  , έχουμε
, έχουμε
 και
και  . Συνεπώς
. Συνεπώς , άρα η
, άρα η  είναι η διχοτόμος της
είναι η διχοτόμος της
 . Παρομοίως,
. Παρομοίως,  , άρα και το τρίγωνο
, άρα και το τρίγωνο  είναι ισοσκελές, άρα
είναι ισοσκελές, άρα  . Από το εγγράψιμο τετράπλευρο
. Από το εγγράψιμο τετράπλευρο  , έχουμε:
, έχουμε: και
και  . Συνεπώς
. Συνεπώς  ,άρα η
,άρα η  είναι η διχοτόμος της
είναι η διχοτόμος της . To σημείο
. To σημείο  είναι το περίκεντρο του τριγώνου
είναι το περίκεντρο του τριγώνου 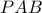 , άρα ανήκει στη μεσοκάθετο του
, άρα ανήκει στη μεσοκάθετο του  .
.
Επομένως, αποδείξαμε ότι, οι εσωτερικές διχοτόμοι των γωνιών και
και  και η μεσοκάθετος του ευθύγραμμου τμήματος
και η μεσοκάθετος του ευθύγραμμου τμήματος  συντρέχουν στο
συντρέχουν στο  .
. 
Έστω
 το κέντρο του περιγεγραμμένου κύκλου του τριγώνου
το κέντρο του περιγεγραμμένου κύκλου του τριγώνου . Θα αποδείξουμε ότι είναι το ζητούμενο σημείο τομής των δεδομένων ευθειών. Έστω
. Θα αποδείξουμε ότι είναι το ζητούμενο σημείο τομής των δεδομένων ευθειών. Έστω  και
και  . Από την υπόθεση θα ισχύει:
. Από την υπόθεση θα ισχύει: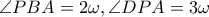 και
και  . Επιπλέον, θα ισχύει
. Επιπλέον, θα ισχύει (ως επίκεντρη που βαίνει στο ίδιο τόξο με την εγγεγραμμένη
(ως επίκεντρη που βαίνει στο ίδιο τόξο με την εγγεγραμμένη ) και
) και (ως επίκεντρη που βαίνει στο ίδιο τόξο με την εγγεγραμμένη
(ως επίκεντρη που βαίνει στο ίδιο τόξο με την εγγεγραμμένη  ). Στο τρίγωνο
). Στο τρίγωνο  :
:  . Επίσης, στο τρίγωνο
. Επίσης, στο τρίγωνο :
:  . Στο τετράπλευρο
. Στο τετράπλευρο  οι απέναντι γωνίες
οι απέναντι γωνίες και
και 
είναι παραπληρωματικές, εφόσον
 . Επομένως είναι εγγράψιμο. Στο τετράπλευρο
. Επομένως είναι εγγράψιμο. Στο τετράπλευρο  , οι απέναντι γωνίες
, οι απέναντι γωνίες  και
και  είναι παραπληρωματικές, εφόσον
είναι παραπληρωματικές, εφόσον  . Eπομένως είναι εγγράψιμο. Παρατηρούμε ότι
. Eπομένως είναι εγγράψιμο. Παρατηρούμε ότι  (ως ακτίνες του περίκυκλου του τριγώνου
(ως ακτίνες του περίκυκλου του τριγώνου ), άρα το τρίγωνο
), άρα το τρίγωνο είναι ισοσκελές, άρα
είναι ισοσκελές, άρα  . Από το εγγράψιμο τετράπλευρο
. Από το εγγράψιμο τετράπλευρο  , έχουμε
, έχουμε και
και  . Συνεπώς
. Συνεπώς , άρα η
, άρα η  είναι η διχοτόμος της
είναι η διχοτόμος της . Παρομοίως,
. Παρομοίως,  , άρα και το τρίγωνο
, άρα και το τρίγωνο  είναι ισοσκελές, άρα
είναι ισοσκελές, άρα  . Από το εγγράψιμο τετράπλευρο
. Από το εγγράψιμο τετράπλευρο  , έχουμε:
, έχουμε: και
και  . Συνεπώς
. Συνεπώς  ,άρα η
,άρα η  είναι η διχοτόμος της
είναι η διχοτόμος της . To σημείο
. To σημείο  είναι το περίκεντρο του τριγώνου
είναι το περίκεντρο του τριγώνου 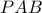 , άρα ανήκει στη μεσοκάθετο του
, άρα ανήκει στη μεσοκάθετο του  .
.Επομένως, αποδείξαμε ότι, οι εσωτερικές διχοτόμοι των γωνιών
 και
και  και η μεσοκάθετος του ευθύγραμμου τμήματος
και η μεσοκάθετος του ευθύγραμμου τμήματος  συντρέχουν στο
συντρέχουν στο  .
. 
τελευταία επεξεργασία από MAnTH05 σε Παρ Νοέμ 13, 2020 9:35 pm, έχει επεξεργασθεί 2 φορές συνολικά.
Ματθαίος Κουκλέρης
Re: ΙΜΟ 2020
Τα αποτελέσματα έχουν δημοσιευτεί. Δεν τα βάζω γιατί μου κολλάει και δεν μπορώ να τα δω αναλυτικά. Πάρα πολλά συγχαρητήρια σε όλα τα παιδιά και των δύο ομάδων μας που σε μία πάρα πολύ δύσκολη χρονιά τα κατάφεραν άψογα!!
Επίσης, δεν μπορώ να μην συγχαρώ τους συνοδούς αλλά και όσους δούλεψαν ώστε να πραγματοποιηθεί αυτή η πρωτότυπη Ολυμπιάδα!
Επίσης, δεν μπορώ να μην συγχαρώ τους συνοδούς αλλά και όσους δούλεψαν ώστε να πραγματοποιηθεί αυτή η πρωτότυπη Ολυμπιάδα!
- matha
- Γενικός Συντονιστής
- Δημοσιεύσεις: 6423
- Εγγραφή: Παρ Μάιος 21, 2010 7:40 pm
- Τοποθεσία: Θεσσαλονίκη
Re: ΙΜΟ 2020
Πολλά συγχαρητήρια σε όλους!
- Συνημμένα
-
- imo.png (60.64 KiB) Προβλήθηκε 2534 φορές
Μάγκος Θάνος
-
Τσιαλας Νικολαος
- Δημοσιεύσεις: 789
- Εγγραφή: Σάβ Ιαν 17, 2015 1:04 pm
Re: ΙΜΟ 2020
Πολλά συγχαρητήρια σε όλα τα παιδια και ιδιαίτερα στους μεγάλους Μίνωα και Διονύση αλλά και στον Ορέστη που είναι μόλις δευτέρα γυμνασίου!! 

-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5561
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
Re: ΙΜΟ 2020
Θερμά συγχαρητήρια στην ομάδα, σε όλα τα παιδιά και στους καθηγητές τους !
Οι νεότεροι έχουν και άλλες ευκαιρίες και θα πάνε ακόμα πιο ψηλά.
Καλή Σχολική και Ακαδημαϊκή χρονιά !
Οι νεότεροι έχουν και άλλες ευκαιρίες και θα πάνε ακόμα πιο ψηλά.
Καλή Σχολική και Ακαδημαϊκή χρονιά !
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13278
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: ΙΜΟ 2020
Συγχαρητήρια σε όλα τα παιδιά, στους καθηγητές τους και στους γονείς τους που τα στηρίζουν!
- S.E.Louridas
- Δημοσιεύσεις: 5956
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
Re: ΙΜΟ 2020
Συγχαρητήρια πολλά και θερμά στους Έλληνες αλλά και Κύπριους διαγωνιζόμενους στην ΙΜΟ 2020. Και μόνο το οδοιπορικό που καταλήγει στη συμμετοχή σε τέτοιο Επιστημονικό διαγωνισμό είναι Μετάλλιο και μία ισχυρή απάντηση στην πρόκληση της εποχής. Τα πλέον ιδιαίτερα συγχαρητήρια στους διαγωνιζόμενους που διακρίθηκαν στον διαγωνισμό αυτό, να ξέρουν ότι είναι φάροι, ελπιδοφόροι, μας συγκινούν και μας κάνουν υπερήφανους.
S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15764
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: ΙΜΟ 2020
ΕΥΓΕ.
Τα θέματα είναι ΠΑΡΑ ΠΟΛΥ ΔΥΣΚΟΛΑ και το γεγονός ότι τα παιδιά μας μπόρεσαν να τα ξεκλειδώσουν, ιδίως στον περιορισμένο χρόνο που τους δίνεται, είναι αξιοθαύμαστο. Εύγε, εύγε, εύγε.
Τα θέματα είναι ΠΑΡΑ ΠΟΛΥ ΔΥΣΚΟΛΑ και το γεγονός ότι τα παιδιά μας μπόρεσαν να τα ξεκλειδώσουν, ιδίως στον περιορισμένο χρόνο που τους δίνεται, είναι αξιοθαύμαστο. Εύγε, εύγε, εύγε.
Re: ΙΜΟ 2020
Θερμά συγχαρητήρια σε όλα τα παιδιά, στους γονείς και στου όποιους δασκάλους τους .
Πολύ ανεβασμένου επιπέδου δέματα και ως εκ τούτου η επιτυχίες τους έχουν βαρύνουσα σημασία .
Γι αυτούς που θα δώσουν και τα επόμενα έτη εύχομαι μεγαλύτερες επιτυχίες !
Πολύ ανεβασμένου επιπέδου δέματα και ως εκ τούτου η επιτυχίες τους έχουν βαρύνουσα σημασία .
Γι αυτούς που θα δώσουν και τα επόμενα έτη εύχομαι μεγαλύτερες επιτυχίες !
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: ΙΜΟ 2020
Συγχαρητήρια και από εμένα. Η Κύπρος είχε τρεις επαίνους με τους Χάρη Γεωργίου, Ιωάννη Χαραλάμπους και Μάριο Αβρααμίδη. Οι Χάρης και Γιάννης έχασαν το χάλκινο για μία μονάδα. 
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: ΙΜΟ 2020
Πολλά συγχαρητήρια στους συμμετέχοντες στην κορυφαία μαθητική διοργάνωση για τα μαθηματικά στον κόσμο!! Όλα τα παιδιά της αποστολής είναι ένας κι ένας!! Χαρηκα ιδιαίτερα που φύγατε όλοι με έπαινο και μετάλλιο... Δεν είναι και λίγο πράγμα να λύνεις πλήρως ένα ολόκληρο πρόβλημα όταν τα θέματα είναι τόσο απαιτητικά!
Σε όσους επιπλέον πήραν και μετάλλιο να τους δώσω διπλά συγχαρητήρια! Δε θα μπορούσα να μην αναφερθώ ξεχωριστά στο Μίνο (που είχα την τύχη να τον έχω μαθητή στο σχολείο μου σε όλες τις τάξεις του Λυκείου, μαθητή για πολλά χρόνια στον όμιλο αριστείας που διοργάνωνε το σχολείο μου σε συνεργασία με το Παράρτημα Ηρακλείου της ΕΜΕ και μέλος - από πολύ μικρή ηλικία - στις ελληνικές αποστολές για τη Βαλκανική Ολυμπιάδα Μαθηματικών όσες φορές έτυχε να τις συνοδεύσω. Πρόκειται για εξαιρετικό παιδί με μεγάλο ταλέντο και πλέον εκκολαπτόμενος συνάδελφος στο Τμήμα Μαθηματικών του Πανεπιστημίου Αθηνών!! Μίνο καλή σταδιοδρομία στην ακαδημαϊκή σου πλέον πορεία...), στο Διονύση και στον Ορέστη αγαπητά μέλη όλοι τους εδώ στο mathematica οι οποίοι το κοσμούν και το ενισχύουν με τις σκέψεις, τις παρεμβάσεις και τις λύσεις τους...
Συγχαρητήρια και στα μέλη της Κυπριακής αποστολής για τη συμμετοχή τους αλλά και τους επαίνους τους!
Σας ευχαριστούμε πολύ για την περηφάνεια που μας κάνετε να νιώθουμε!
Αλέξανδρος
Σε όσους επιπλέον πήραν και μετάλλιο να τους δώσω διπλά συγχαρητήρια! Δε θα μπορούσα να μην αναφερθώ ξεχωριστά στο Μίνο (που είχα την τύχη να τον έχω μαθητή στο σχολείο μου σε όλες τις τάξεις του Λυκείου, μαθητή για πολλά χρόνια στον όμιλο αριστείας που διοργάνωνε το σχολείο μου σε συνεργασία με το Παράρτημα Ηρακλείου της ΕΜΕ και μέλος - από πολύ μικρή ηλικία - στις ελληνικές αποστολές για τη Βαλκανική Ολυμπιάδα Μαθηματικών όσες φορές έτυχε να τις συνοδεύσω. Πρόκειται για εξαιρετικό παιδί με μεγάλο ταλέντο και πλέον εκκολαπτόμενος συνάδελφος στο Τμήμα Μαθηματικών του Πανεπιστημίου Αθηνών!! Μίνο καλή σταδιοδρομία στην ακαδημαϊκή σου πλέον πορεία...), στο Διονύση και στον Ορέστη αγαπητά μέλη όλοι τους εδώ στο mathematica οι οποίοι το κοσμούν και το ενισχύουν με τις σκέψεις, τις παρεμβάσεις και τις λύσεις τους...
Συγχαρητήρια και στα μέλη της Κυπριακής αποστολής για τη συμμετοχή τους αλλά και τους επαίνους τους!
Σας ευχαριστούμε πολύ για την περηφάνεια που μας κάνετε να νιώθουμε!
Αλέξανδρος
Αλέξανδρος Συγκελάκης
-
Λάμπρος Κατσάπας
- Δημοσιεύσεις: 838
- Εγγραφή: Σάβ Ιουν 17, 2017 10:17 pm
- Τοποθεσία: Αθήνα
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: ΙΜΟ 2020
Βάζω τη λύση μου και στο πρόβλημα 4.
Θα δώσω αρχικά ένα παράδειγμα με τελεφερίκ σε κάθε εταιρεία όπου δεν υπάρχουν δύο σταθμοί οι οποίοι να συνδέονται και με τις δύο εταιρείες. Ονομάζω τους σταθμούς
τελεφερίκ σε κάθε εταιρεία όπου δεν υπάρχουν δύο σταθμοί οι οποίοι να συνδέονται και με τις δύο εταιρείες. Ονομάζω τους σταθμούς  με τον
με τον  να είναι ο χαμηλότερος και ο
να είναι ο χαμηλότερος και ο  ο ψηλότερος.
ο ψηλότερος.
Η εταιρεία Α έχει τα τελεφερίκ από τον σταθμό στον σταθμό
στον σταθμό  για κάθε
για κάθε  με
με  . Συνολικά
. Συνολικά  τελεφερίκ. Μπορεί κάποιος να πάει από ένα σταθμό σε άλλον μέσω των τελεφερίκ της
τελεφερίκ. Μπορεί κάποιος να πάει από ένα σταθμό σε άλλον μέσω των τελεφερίκ της  αν και μόνο αν και οι δύο σταθμοί ανήκουν στο ίδιο από τα πιο κάτω σύνολα:
αν και μόνο αν και οι δύο σταθμοί ανήκουν στο ίδιο από τα πιο κάτω σύνολα:  .
.
Η εταιρεία B έχει τα τελεφερίκ από τον σταθμό στον σταθμό
στον σταθμό  για κάθε
για κάθε  . Συνολικά
. Συνολικά  τελεφερίκ. Μπορεί κάποιος να πάει από ένα σταθμό σε άλλον μέσω των τελεφερίκ της
τελεφερίκ. Μπορεί κάποιος να πάει από ένα σταθμό σε άλλον μέσω των τελεφερίκ της  αν και μόνο αν και οι δύο σταθμοί αφήνουν το ίδιο υπόλοιπο modulo
αν και μόνο αν και οι δύο σταθμοί αφήνουν το ίδιο υπόλοιπο modulo  .
.
Βλέπουμε λοιπόν ότι δεν υπάρχουν σταθμοί οι οποίοι να συνδέονται και από τις δύο εταιρείες.
Αναγκαστικά λοιπόν πρέπει . Θα δείξουμε ότι σε αυτήν την περίπτωση υπάρχουν δύο σταθμοί οι οποίοι να συνδέονται και από τις δύο εταιρείες. Θεωρούμε ένα γράφημα με κορυφές τους σταθμούς όπου συνδέουμε δύο σταθμούς αν και μόνο αν υπάρχει τελεφερίκ της εταιρείας
. Θα δείξουμε ότι σε αυτήν την περίπτωση υπάρχουν δύο σταθμοί οι οποίοι να συνδέονται και από τις δύο εταιρείες. Θεωρούμε ένα γράφημα με κορυφές τους σταθμούς όπου συνδέουμε δύο σταθμούς αν και μόνο αν υπάρχει τελεφερίκ της εταιρείας  που σε πηγαίνει από τον ένα στον άλλο. Το γράφημα έχει
που σε πηγαίνει από τον ένα στον άλλο. Το γράφημα έχει  ακμές και δεν μπορεί να έχει κύκλο. Είναι λοιπόν δάσος με
ακμές και δεν μπορεί να έχει κύκλο. Είναι λοιπόν δάσος με  συνεκτικές συνιστώσες. Σε κάθε συνιστώσα μπορούμε να ταξιδέψουμε από οποιαδήποτε κορυφή σε οποιαδήποτε άλλη μέσω της εταιρείας
συνεκτικές συνιστώσες. Σε κάθε συνιστώσα μπορούμε να ταξιδέψουμε από οποιαδήποτε κορυφή σε οποιαδήποτε άλλη μέσω της εταιρείας  . Από την αρχή του περιστερώνα, σε μία από τις συνιστώσες πρέπει να έχουμε τουλάχιστον
. Από την αρχή του περιστερώνα, σε μία από τις συνιστώσες πρέπει να έχουμε τουλάχιστον  σταθμούς. Έστω οι σταθμοί
σταθμούς. Έστω οι σταθμοί  .
.
Όμως με το ίδιο σκεπτικό έχουμε και συνεκτικές συνιστώσες στο γράφημα της εταιρείας
συνεκτικές συνιστώσες στο γράφημα της εταιρείας  . Δύο όμως από τους
. Δύο όμως από τους  θα ανήκουν αναγκαστικά στην ίδια συνιστώσα του
θα ανήκουν αναγκαστικά στην ίδια συνιστώσα του  . Αυτοί οι δύο σταθμοί συνδέονται και από τις δύο εταιρείες οπότε τελειώσαμε.
. Αυτοί οι δύο σταθμοί συνδέονται και από τις δύο εταιρείες οπότε τελειώσαμε.
Θα δώσω αρχικά ένα παράδειγμα με
 τελεφερίκ σε κάθε εταιρεία όπου δεν υπάρχουν δύο σταθμοί οι οποίοι να συνδέονται και με τις δύο εταιρείες. Ονομάζω τους σταθμούς
τελεφερίκ σε κάθε εταιρεία όπου δεν υπάρχουν δύο σταθμοί οι οποίοι να συνδέονται και με τις δύο εταιρείες. Ονομάζω τους σταθμούς  με τον
με τον  να είναι ο χαμηλότερος και ο
να είναι ο χαμηλότερος και ο  ο ψηλότερος.
ο ψηλότερος.Η εταιρεία Α έχει τα τελεφερίκ από τον σταθμό
 στον σταθμό
στον σταθμό  για κάθε
για κάθε  με
με  . Συνολικά
. Συνολικά  τελεφερίκ. Μπορεί κάποιος να πάει από ένα σταθμό σε άλλον μέσω των τελεφερίκ της
τελεφερίκ. Μπορεί κάποιος να πάει από ένα σταθμό σε άλλον μέσω των τελεφερίκ της  αν και μόνο αν και οι δύο σταθμοί ανήκουν στο ίδιο από τα πιο κάτω σύνολα:
αν και μόνο αν και οι δύο σταθμοί ανήκουν στο ίδιο από τα πιο κάτω σύνολα:  .
.Η εταιρεία B έχει τα τελεφερίκ από τον σταθμό
 στον σταθμό
στον σταθμό  για κάθε
για κάθε  . Συνολικά
. Συνολικά  τελεφερίκ. Μπορεί κάποιος να πάει από ένα σταθμό σε άλλον μέσω των τελεφερίκ της
τελεφερίκ. Μπορεί κάποιος να πάει από ένα σταθμό σε άλλον μέσω των τελεφερίκ της  αν και μόνο αν και οι δύο σταθμοί αφήνουν το ίδιο υπόλοιπο modulo
αν και μόνο αν και οι δύο σταθμοί αφήνουν το ίδιο υπόλοιπο modulo  .
.Βλέπουμε λοιπόν ότι δεν υπάρχουν σταθμοί οι οποίοι να συνδέονται και από τις δύο εταιρείες.
Αναγκαστικά λοιπόν πρέπει
 . Θα δείξουμε ότι σε αυτήν την περίπτωση υπάρχουν δύο σταθμοί οι οποίοι να συνδέονται και από τις δύο εταιρείες. Θεωρούμε ένα γράφημα με κορυφές τους σταθμούς όπου συνδέουμε δύο σταθμούς αν και μόνο αν υπάρχει τελεφερίκ της εταιρείας
. Θα δείξουμε ότι σε αυτήν την περίπτωση υπάρχουν δύο σταθμοί οι οποίοι να συνδέονται και από τις δύο εταιρείες. Θεωρούμε ένα γράφημα με κορυφές τους σταθμούς όπου συνδέουμε δύο σταθμούς αν και μόνο αν υπάρχει τελεφερίκ της εταιρείας  που σε πηγαίνει από τον ένα στον άλλο. Το γράφημα έχει
που σε πηγαίνει από τον ένα στον άλλο. Το γράφημα έχει  ακμές και δεν μπορεί να έχει κύκλο. Είναι λοιπόν δάσος με
ακμές και δεν μπορεί να έχει κύκλο. Είναι λοιπόν δάσος με  συνεκτικές συνιστώσες. Σε κάθε συνιστώσα μπορούμε να ταξιδέψουμε από οποιαδήποτε κορυφή σε οποιαδήποτε άλλη μέσω της εταιρείας
συνεκτικές συνιστώσες. Σε κάθε συνιστώσα μπορούμε να ταξιδέψουμε από οποιαδήποτε κορυφή σε οποιαδήποτε άλλη μέσω της εταιρείας  . Από την αρχή του περιστερώνα, σε μία από τις συνιστώσες πρέπει να έχουμε τουλάχιστον
. Από την αρχή του περιστερώνα, σε μία από τις συνιστώσες πρέπει να έχουμε τουλάχιστον  σταθμούς. Έστω οι σταθμοί
σταθμούς. Έστω οι σταθμοί  .
.Όμως με το ίδιο σκεπτικό έχουμε και
 συνεκτικές συνιστώσες στο γράφημα της εταιρείας
συνεκτικές συνιστώσες στο γράφημα της εταιρείας  . Δύο όμως από τους
. Δύο όμως από τους  θα ανήκουν αναγκαστικά στην ίδια συνιστώσα του
θα ανήκουν αναγκαστικά στην ίδια συνιστώσα του  . Αυτοί οι δύο σταθμοί συνδέονται και από τις δύο εταιρείες οπότε τελειώσαμε.
. Αυτοί οι δύο σταθμοί συνδέονται και από τις δύο εταιρείες οπότε τελειώσαμε.- Διονύσιος Αδαμόπουλος
- Δημοσιεύσεις: 807
- Εγγραφή: Σάβ Μαρ 19, 2016 5:11 pm
- Τοποθεσία: Πύργος Ηλείας
Re: ΙΜΟ 2020
Όλη η ομάδα ευχαριστούμε για τα καλά σας λόγια! Ήταν πράγματι ένας δύσκολος διαγωνισμός, τόσο λόγω των συνθηκών της πανδημίας, όσο και των θεμάτων που έπεσαν τα οποία ήταν αρκετά έξω από τα νερά μας με πολλά combinatorics!
Εγώ προσωπικά θέλω να ευχαριστήσω τα μέλη του mathematica και για την ενθάρρυνσή τους όλα αυτά τα χρόνια αλλά και το χρήσιμο υλικό που συνεχώς ανέβαζαν. Μάλιστα ήταν αρκετοί αυτοί που αποτελούσαν και συνεχίζουν να αποτελούν πρότυπο και πηγή έμπνευσης.
Εγώ προσωπικά θέλω να ευχαριστήσω τα μέλη του mathematica και για την ενθάρρυνσή τους όλα αυτά τα χρόνια αλλά και το χρήσιμο υλικό που συνεχώς ανέβαζαν. Μάλιστα ήταν αρκετοί αυτοί που αποτελούσαν και συνεχίζουν να αποτελούν πρότυπο και πηγή έμπνευσης.
Houston, we have a problem!
Re: ΙΜΟ 2020
Να ευχαριστήσω και γω με τη σειρά μου το  ,από τους "φτασμένους" μέχρι και τους νεώτερους για τη συνολική προσφορά.Κυρίως βέβαια τους κ.Βαρβεράκη/Συγκελάκη από το παράρτημα Ηρακλείου ,καθώς και οποιονδήποτε άλλο συνεισφέρει ανιδιοτελώς προς τη διαμόρφωση αυτής της ιδιαίτερης "Εκπαιδευτικής διαδικασίας" γύρω από τα Μαθηματικά.(διόλου τετριμμένο δεδομένων των συνθηκών).
,από τους "φτασμένους" μέχρι και τους νεώτερους για τη συνολική προσφορά.Κυρίως βέβαια τους κ.Βαρβεράκη/Συγκελάκη από το παράρτημα Ηρακλείου ,καθώς και οποιονδήποτε άλλο συνεισφέρει ανιδιοτελώς προς τη διαμόρφωση αυτής της ιδιαίτερης "Εκπαιδευτικής διαδικασίας" γύρω από τα Μαθηματικά.(διόλου τετριμμένο δεδομένων των συνθηκών).
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες
