EGMO 2020
Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
EGMO 2020
Η EGMO που θα διεξαγόταν αυτές τις μέρες στην Ολλανδία διεξάγεται τώρα διαδικτυακά. Μπορείτε να βρείτε περισσότερες πληροφορίες στην ιστοσελίδα του διαγωνισμού. Αν θέλετε περισσότερες πληροφορίες να σας τις λύσουμε εγώ ή ο Αχιλλέας που είναι αρχηγός της Ελληνικής αποστολής.
Αυτή τη στιγμή τα κορίτσια της Κύπρου και της Ελλάδας γράφουν το γραπτό της δεύτερης μέρας του διαγωνισμού. Ας τους ευχηθούμε λοιπόν καλή επιτυχία.
Όσον αφορά τα θέματα θα πρέπει να κάνετε λίγη υπομονή. Δεν μπορούμε να τα μοιραστούμε πριν τα ξημερώματα της Κυριακής μιας και υπάρχει περιθώριο μέχρι τότε για τις χώρες να κάνουν το διαγωνισμό τους.
Αυτή τη στιγμή τα κορίτσια της Κύπρου και της Ελλάδας γράφουν το γραπτό της δεύτερης μέρας του διαγωνισμού. Ας τους ευχηθούμε λοιπόν καλή επιτυχία.
Όσον αφορά τα θέματα θα πρέπει να κάνετε λίγη υπομονή. Δεν μπορούμε να τα μοιραστούμε πριν τα ξημερώματα της Κυριακής μιας και υπάρχει περιθώριο μέχρι τότε για τις χώρες να κάνουν το διαγωνισμό τους.
Λέξεις Κλειδιά:
-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5561
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
Re: EGMO 2020
Καλή Επιτυχία στα κορίτσια μας !Demetres έγραψε: ↑Παρ Απρ 17, 2020 10:42 amΗ EGMO που θα διεξαγόταν αυτές τις μέρες στην Ολλανδία διεξάγεται τώρα διαδικτυακά. Μπορείτε να βρείτε περισσότερες πληροφορίες στην ιστοσελίδα του διαγωνισμού. Αν θέλετε περισσότερες πληροφορίες να σας τις λύσουμε εγώ ή ο Αχιλλέας που είναι αρχηγός της Ελληνικής αποστολής.
Αυτή τη στιγμή τα κορίτσια της Κύπρου και της Ελλάδας γράφουν το γραπτό της δεύτερης μέρας του διαγωνισμού. Ας τους ευχηθούμε λοιπόν καλή επιτυχία.
Όσον αφορά τα θέματα θα πρέπει να κάνετε λίγη υπομονή. Δεν μπορούμε να τα μοιραστούμε πριν τα ξημερώματα της Κυριακής μιας και υπάρχει περιθώριο μέχρι τότε για τις χώρες να κάνουν το διαγωνισμό τους.
Εϊναι εξαιρετικός διαγωνισμός με πολύ ωραία θέματα.
ΚΑΛΗ ΑΝΑΣΤΑΣΗ !!!
-
Τσιαλας Νικολαος
- Δημοσιεύσεις: 789
- Εγγραφή: Σάβ Ιαν 17, 2015 1:04 pm
Re: EGMO 2020
Καλημέρα και Χρόνια Πολλά!
ΠΡΩΤΗ ΗΜΕΡΑ
Πρόβλημα 1. Οι θετικοί ακέραιοι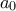 ,
,  ,
, 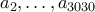 ικανοποιούν τη συνθήκη
ικανοποιούν τη συνθήκη
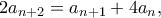
για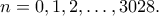 Να αποδειχθεί ότι τουλάχιστον ένας από τους αριθμούς
Να αποδειχθεί ότι τουλάχιστον ένας από τους αριθμούς 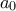 ,
,  ,
,  ,
, 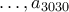 διαιρείται με το
διαιρείται με το  .
.
Πρόβλημα 2. Να βρείτε όλες τις λίστες μη-αρνητικών πραγματικών αριθμών τέτοιων ώστε να ικανοποιούνται όλες οι παρακάτω συνθήκες:
μη-αρνητικών πραγματικών αριθμών τέτοιων ώστε να ικανοποιούνται όλες οι παρακάτω συνθήκες:
(i)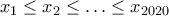 ,
,
(ii)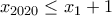 ,
,
(iii) υπάρχει μετάθεση της
της  τέτοια ώστε
τέτοια ώστε

Μετάθεση μιας λίστας είναι μια λίστα ιδίου μήκους, με τα ίδια στοιχεία, τα οποία επιτρέπεται να είναι σε οποιαδήποτε σειρά. Για παράδειγμα, η είναι μια μετάθεση της
είναι μια μετάθεση της 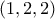 . Επιπλέον, και οι δύο είναι μεταθέσεις της
. Επιπλέον, και οι δύο είναι μεταθέσεις της  . Παρατηρήστε ότι κάθε λίστα είναι μετάθεση του εαυτού της.
. Παρατηρήστε ότι κάθε λίστα είναι μετάθεση του εαυτού της.
Πρόβλημα 3.
Έστω κυρτό εξάγωνο τέτοιο ώστε
τέτοιο ώστε  και
και  και οι (εσωτερικές) διχοτόμοι των
και οι (εσωτερικές) διχοτόμοι των  ,
,  , και
, και  συντρέχουν.
συντρέχουν.
Να αποδειχθεί ότι οι (εσωτερικές) διχοτόμοι των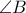 ,
,  , και
, και  επίσης συντρέχουν.
επίσης συντρέχουν.
Παρατηρήστε ότι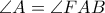 . Οι άλλες εσωτερικές γωνίες του εξαγώνου ορίζονται ομοίως.
. Οι άλλες εσωτερικές γωνίες του εξαγώνου ορίζονται ομοίως.
ΠΡΩΤΗ ΗΜΕΡΑ
Πρόβλημα 1. Οι θετικοί ακέραιοι
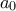 ,
,  ,
, 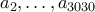 ικανοποιούν τη συνθήκη
ικανοποιούν τη συνθήκη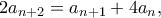
για
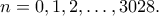 Να αποδειχθεί ότι τουλάχιστον ένας από τους αριθμούς
Να αποδειχθεί ότι τουλάχιστον ένας από τους αριθμούς 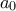 ,
,  ,
,  ,
, 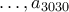 διαιρείται με το
διαιρείται με το  .
.Πρόβλημα 2. Να βρείτε όλες τις λίστες
 μη-αρνητικών πραγματικών αριθμών τέτοιων ώστε να ικανοποιούνται όλες οι παρακάτω συνθήκες:
μη-αρνητικών πραγματικών αριθμών τέτοιων ώστε να ικανοποιούνται όλες οι παρακάτω συνθήκες:(i)
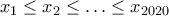 ,
,(ii)
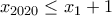 ,
,(iii) υπάρχει μετάθεση
 της
της  τέτοια ώστε
τέτοια ώστε
Μετάθεση μιας λίστας είναι μια λίστα ιδίου μήκους, με τα ίδια στοιχεία, τα οποία επιτρέπεται να είναι σε οποιαδήποτε σειρά. Για παράδειγμα, η
 είναι μια μετάθεση της
είναι μια μετάθεση της 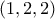 . Επιπλέον, και οι δύο είναι μεταθέσεις της
. Επιπλέον, και οι δύο είναι μεταθέσεις της  . Παρατηρήστε ότι κάθε λίστα είναι μετάθεση του εαυτού της.
. Παρατηρήστε ότι κάθε λίστα είναι μετάθεση του εαυτού της.Πρόβλημα 3.
Έστω κυρτό εξάγωνο
 τέτοιο ώστε
τέτοιο ώστε  και
και  και οι (εσωτερικές) διχοτόμοι των
και οι (εσωτερικές) διχοτόμοι των  ,
,  , και
, και  συντρέχουν.
συντρέχουν.Να αποδειχθεί ότι οι (εσωτερικές) διχοτόμοι των
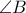 ,
,  , και
, και  επίσης συντρέχουν.
επίσης συντρέχουν.Παρατηρήστε ότι
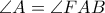 . Οι άλλες εσωτερικές γωνίες του εξαγώνου ορίζονται ομοίως.
. Οι άλλες εσωτερικές γωνίες του εξαγώνου ορίζονται ομοίως.Re: EGMO 2020
ΔΕΥΤΕΡΗ ΗΜΕΡΑ
Πρόβλημα 4. Μια μετάθεση των ακεραίων ,
, 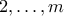 ονομάζεται φρέσκια εάν δεν υπάρχει θετικός ακέραιος
ονομάζεται φρέσκια εάν δεν υπάρχει θετικός ακέραιος  τέτοιος ώστε οι πρώτοι
τέτοιος ώστε οι πρώτοι  αριθμοί στη μετάθεση να είναι οι
αριθμοί στη μετάθεση να είναι οι  ,
, 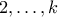 σε κάποια σειρά. Έστω
σε κάποια σειρά. Έστω  το πλήθος των φρέσκων μεταθέσεων των ακεραίων
το πλήθος των φρέσκων μεταθέσεων των ακεραίων  ,
, 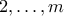 .
.
Να αποδειχθεί ότι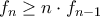 για κάθε
για κάθε  .
.
Για παράδειγμα, αν , τότε η μετάθεση
, τότε η μετάθεση 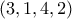 είναι φρέσκια, ενώ η μετάθεση
είναι φρέσκια, ενώ η μετάθεση  δεν είναι.
δεν είναι.
Πρόβλημα 5.
Θεωρούμε τρίγωνο με
με 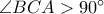 . Ο περιγεγραμμένος κύκλος
. Ο περιγεγραμμένος κύκλος  του
του  έχει ακτίνα
έχει ακτίνα  . Υπάρχει σημείο
. Υπάρχει σημείο  στο εσωτερικό του τμήματος
στο εσωτερικό του τμήματος  τέτοιο ώστε
τέτοιο ώστε  και το μήκος του
και το μήκος του  ισούται με
ισούται με  . Η μεσοκάθετος του
. Η μεσοκάθετος του  τέμνει τον
τέμνει τον  στα σημεία
στα σημεία  και
και  .
.
Να αποδειχθεί ότι το είναι το έγκεντρο του τριγώνου
είναι το έγκεντρο του τριγώνου  .
.
Πρόβλημα 6. Έστω ακέραιος . Η ακολουθία
. Η ακολουθία 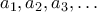 ορίζεται με
ορίζεται με 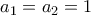 ,
,
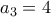 , και για κάθε
, και για κάθε  ,
,
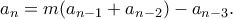
Να βρεθούν όλοι οι ακέραιοι τέτοιοι ώστε κάθε όρος της ακολουθίας να είναι τέλειο τετράγωνο.
τέτοιοι ώστε κάθε όρος της ακολουθίας να είναι τέλειο τετράγωνο.
Πρόβλημα 4. Μια μετάθεση των ακεραίων
 ,
, 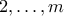 ονομάζεται φρέσκια εάν δεν υπάρχει θετικός ακέραιος
ονομάζεται φρέσκια εάν δεν υπάρχει θετικός ακέραιος  τέτοιος ώστε οι πρώτοι
τέτοιος ώστε οι πρώτοι  αριθμοί στη μετάθεση να είναι οι
αριθμοί στη μετάθεση να είναι οι  ,
, 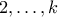 σε κάποια σειρά. Έστω
σε κάποια σειρά. Έστω  το πλήθος των φρέσκων μεταθέσεων των ακεραίων
το πλήθος των φρέσκων μεταθέσεων των ακεραίων  ,
, 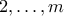 .
.Να αποδειχθεί ότι
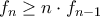 για κάθε
για κάθε  .
.Για παράδειγμα, αν
 , τότε η μετάθεση
, τότε η μετάθεση 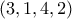 είναι φρέσκια, ενώ η μετάθεση
είναι φρέσκια, ενώ η μετάθεση  δεν είναι.
δεν είναι.Πρόβλημα 5.
Θεωρούμε τρίγωνο
 με
με 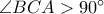 . Ο περιγεγραμμένος κύκλος
. Ο περιγεγραμμένος κύκλος  του
του  έχει ακτίνα
έχει ακτίνα  . Υπάρχει σημείο
. Υπάρχει σημείο  στο εσωτερικό του τμήματος
στο εσωτερικό του τμήματος  τέτοιο ώστε
τέτοιο ώστε  και το μήκος του
και το μήκος του  ισούται με
ισούται με  . Η μεσοκάθετος του
. Η μεσοκάθετος του  τέμνει τον
τέμνει τον  στα σημεία
στα σημεία  και
και  .
.Να αποδειχθεί ότι το
 είναι το έγκεντρο του τριγώνου
είναι το έγκεντρο του τριγώνου  .
.Πρόβλημα 6. Έστω ακέραιος
 . Η ακολουθία
. Η ακολουθία 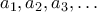 ορίζεται με
ορίζεται με 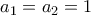 ,
,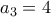 , και για κάθε
, και για κάθε  ,
,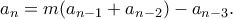
Να βρεθούν όλοι οι ακέραιοι
 τέτοιοι ώστε κάθε όρος της ακολουθίας να είναι τέλειο τετράγωνο.
τέτοιοι ώστε κάθε όρος της ακολουθίας να είναι τέλειο τετράγωνο.- ΦΩΤΙΑΔΗΣ ΠΡΟΔΡΟΜΟΣ
- Δημοσιεύσεις: 921
- Εγγραφή: Πέμ Νοέμ 22, 2018 9:43 pm
Re: EGMO 2020
Στο τρίγωνοachilleas έγραψε: ↑Κυρ Απρ 19, 2020 9:28 am
Πρόβλημα 5.
Θεωρούμε τρίγωνομε
. Ο περιγεγραμμένος κύκλος
του
έχει ακτίνα
. Υπάρχει σημείο
στο εσωτερικό του τμήματος
τέτοιο ώστε
και το μήκος του
ισούται με
. Η μεσοκάθετος του
τέμνει τον
στα σημεία
και
.
Να αποδειχθεί ότι τοείναι το έγκεντρο του τριγώνου
.
 το
το  ανήκει στο ύψος από το
ανήκει στο ύψος από το  και το συμμετρικό αυτού ως προς την
και το συμμετρικό αυτού ως προς την 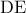 ανήκει στον περίκυκλο του τριγώνου άρα είναι ορθόκεντρο.Έστω
ανήκει στον περίκυκλο του τριγώνου άρα είναι ορθόκεντρο.Έστω 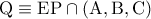 .
.Είναι
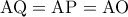 άρα
άρα 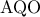 ισόπλευρο.Επίσης
ισόπλευρο.Επίσης 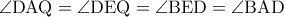 άρα
άρα 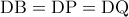 και
και 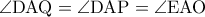 άρα
άρα 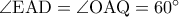 άρα
άρα 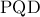 ισόπλευρο.
ισόπλευρο.Είναι
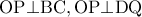 άρα
άρα  και
και 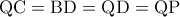 που εξασφαλίζει ότι
που εξασφαλίζει ότι 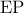 διχοτόμος της
διχοτόμος της  και
και  έκκεντρο του
έκκεντρο του 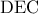
Re: EGMO 2020
Έστωachilleas έγραψε: ↑Κυρ Απρ 19, 2020 9:28 amΔΕΥΤΕΡΗ ΗΜΕΡΑ
Πρόβλημα 4. Μια μετάθεση των ακεραίων,
ονομάζεται φρέσκια εάν δεν υπάρχει θετικός ακέραιος
τέτοιος ώστε οι πρώτοι
αριθμοί στη μετάθεση να είναι οι
,
σε κάποια σειρά. Έστω
το πλήθος των φρέσκων μεταθέσεων των ακεραίων
,
.
Να αποδειχθεί ότιγια κάθε
.
Για παράδειγμα, αν, τότε η μετάθεση
είναι φρέσκια, ενώ η μετάθεση
δεν είναι.
...
 και έστω
και έστω  ,
, 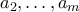 μια φρέσκια μετάθεση των ακεραίων
μια φρέσκια μετάθεση των ακεραίων  ,
, 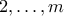 . Παρατηρούμε ότι
. Παρατηρούμε ότι 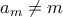 αφού αλλιώς οι
αφού αλλιώς οι  ,
,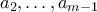 θα αποτελούσαν μετάθεση των
θα αποτελούσαν μετάθεση των  ,
, 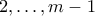 , άτοπο από την υπόθεση μας.
, άτοπο από την υπόθεση μας.Για να πάρουμε μια φρέσκια μετάθεση των
 ,
, 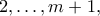 τοποθετούμε τον αριθμό
τοποθετούμε τον αριθμό  πριν το
πριν το  ή ανάμεσα στο
ή ανάμεσα στο  και το
και το  για
για 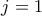 έως
έως  . Εύκολα βλέπουμε ότι κάθε τέτοια μετάθεση είναι φρέσκια.
. Εύκολα βλέπουμε ότι κάθε τέτοια μετάθεση είναι φρέσκια.Καμιά από τις παραπάνω φρέσκιες μεταθέσεις των
 ,
, 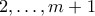 δεν έχει τον
δεν έχει τον  ως τελευταίο στοιχείο. Έστω
ως τελευταίο στοιχείο. Έστω 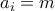 για κάποιο
για κάποιο 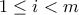 . Τότε μπορούμε να αντικαταστήσουμε το
. Τότε μπορούμε να αντικαταστήσουμε το 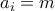 με
με  και να τοποθετήσουμε το
και να τοποθετήσουμε το  στην τελευταία θέση:
στην τελευταία θέση:
Εύκολα βλέπουμε ότι κάθε τέτοια μετάθεση των
 ,
, 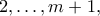 είναι φρέσκια και διαφορετική από τις
είναι φρέσκια και διαφορετική από τις  φρέσκιες μεταθέσεις που πήραμε παραπάνω (οι οποίες λήγουν σε
φρέσκιες μεταθέσεις που πήραμε παραπάνω (οι οποίες λήγουν σε 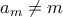 ).
). Επομένως, κάθε φρέσκια μετάθεση των
 ,
, 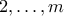 παράγει τουλάχιστον
παράγει τουλάχιστον  φρέσκιες μεταθέσεις των
φρέσκιες μεταθέσεις των  ,
, 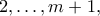 που σημαίνει ότι
που σημαίνει ότι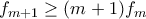
για κάθε
 , όπως θέλαμε.
, όπως θέλαμε.Φιλικά,
Αχιλλέας
Re: EGMO 2020
Θα αποδείξουμε με επαγωγή επί του
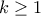 τον παρακάτω ισχυρισμό
τον παρακάτω ισχυρισμόΔοθέντων θετικών ακεραίων
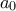 ,
,  ,
,  τέτοιων ώστε
τέτοιων ώστε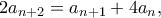
για
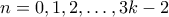 , ο
, ο 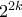 διαιρεί τουλάχιστον έναν από τους
διαιρεί τουλάχιστον έναν από τους 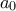 ,
,  ,
,  .
.Πράγματι, για
 έχουμε
έχουμε 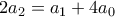 και
και 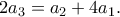 Η δεύτερη ισότητα δίνει ότι ο
Η δεύτερη ισότητα δίνει ότι ο  είναι άρτιος, και από την πρώτη έπεται τότε ότι ο
είναι άρτιος, και από την πρώτη έπεται τότε ότι ο  διαιρείται με το
διαιρείται με το 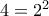 . Άρα ο ισχυρισμός μας αληθεύει για
. Άρα ο ισχυρισμός μας αληθεύει για  .
. Ας υποθέσουμε ότι για κάποιο
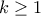 , ο ισχυρισμός μας αληθεύει για κάθε ακολουθία
, ο ισχυρισμός μας αληθεύει για κάθε ακολουθία  θετικών ακεραίων οι οποίοι ικανοποιούν αντίστοιχες αναδρομικές σχέσεις. Θεωρούμε
θετικών ακεραίων οι οποίοι ικανοποιούν αντίστοιχες αναδρομικές σχέσεις. Θεωρούμε 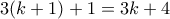 θετικούς ακεραίους
θετικούς ακεραίους 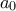 ,
,  ,
, 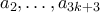 τέτοιους ώστε
τέτοιους ώστε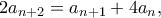
για
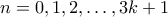 . Βλέπουμε ότι όλοι οι αριθμοί
. Βλέπουμε ότι όλοι οι αριθμοί  ,
,  είναι άρτιοι, οπότε μπορούμε να γράψουμε
είναι άρτιοι, οπότε μπορούμε να γράψουμε 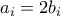 για κάποιους θετικούς ακεραίους
για κάποιους θετικούς ακεραίους  για
για  . Η
. Η 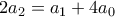 γίνεται
γίνεται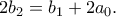
Επίσης, παρατηρούμε ότι
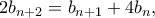
για
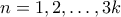 .
.Επόμενως, οι θετικοί ακέραιοι
 ,
, 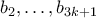 είναι άρτιοι και μπορούμε να γράψουμε
είναι άρτιοι και μπορούμε να γράψουμε 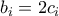 για κάποιους θετικούς ακεραίους
για κάποιους θετικούς ακεραίους 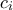 για
για  . Τότε η
. Τότε η 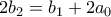 γίνεται
γίνεται  η οποία δεν μας δίνει τίποτα. Όμως έχουμε
η οποία δεν μας δίνει τίποτα. Όμως έχουμε
για
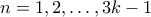 .
.Έτσι η ακολουθία
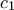 ,
, 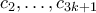 είναι μια ακολουθία
είναι μια ακολουθία  θετικών ακεραίων που ικανοποιούν αντίστοιχες αναδρομικές σχέσεις με αυτές του προβλήματος.
θετικών ακεραίων που ικανοποιούν αντίστοιχες αναδρομικές σχέσεις με αυτές του προβλήματος. Από την επαγωγική υπόθεση, ο
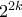 διαιρεί τουλάχιστον έναν εκ των
διαιρεί τουλάχιστον έναν εκ των 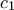 ,
, 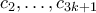 . Αφού
. Αφού 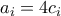 για όλα τα
για όλα τα  , έπεται ότι ο
, έπεται ότι ο 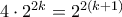 διαρεί τουλάχιστον έναν εκ των
διαρεί τουλάχιστον έναν εκ των 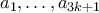 .
.Το συμπέρασμα αυτό ολοκληρώνει την επαγωγή, κι άρα και την απόδειξη.
Φιλικά,
Αχιλλέας
Re: EGMO 2020
Έστω ότι η προέκταση τηςachilleas έγραψε: ↑Κυρ Απρ 19, 2020 9:28 am
Πρόβλημα 5.
Θεωρούμε τρίγωνομε
. Ο περιγεγραμμένος κύκλος
του
έχει ακτίνα
. Υπάρχει σημείο
στο εσωτερικό του τμήματος
τέτοιο ώστε
και το μήκος του
ισούται με
. Η μεσοκάθετος του
τέμνει τον
στα σημεία
και
.
Να αποδειχθεί ότι τοείναι το έγκεντρο του τριγώνου
.
..
 τέμνει τον περιγεγραμμένο κύκλο του
τέμνει τον περιγεγραμμένο κύκλο του  στο
στο  . Αφού
. Αφού  , έχουμε
, έχουμε 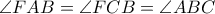 , και
, και 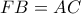 . Άρα το εγγεγραμμένο τετράπλευρο
. Άρα το εγγεγραμμένο τετράπλευρο  είναι ισοσκελές τραπέζιο με
είναι ισοσκελές τραπέζιο με 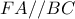 .
. Αφού η ευθεία
 είναι η μεσοκάθετος της χορδής
είναι η μεσοκάθετος της χορδής  και η
και η  είναι παράλληληστη
είναι παράλληληστη  , έπεται ότι η
, έπεται ότι η  είναι κάθετη στην
είναι κάθετη στην  . Αφού
. Αφού 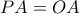 , η ευθεία
, η ευθεία  είναι η μεσοκάθετος του
είναι η μεσοκάθετος του  .
. Επιπλέον, παρατηρούμε ότι το τετράπλευρο
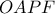 είναι ρόμβος, αφού έχει όλες τις πλευρές του ίσες. Αφού η
είναι ρόμβος, αφού έχει όλες τις πλευρές του ίσες. Αφού η  είναι παράλληλη στην
είναι παράλληλη στην  και
και 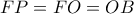 , το τετράπλευρο
, το τετράπλευρο 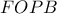 είναι ισοσκελές τραπέζιο. Έτσι, η μεσοκάθετος της βάσης του
είναι ισοσκελές τραπέζιο. Έτσι, η μεσοκάθετος της βάσης του  θα συμπίπτει με την μεσοκάθετο της βάσης του
θα συμπίπτει με την μεσοκάθετο της βάσης του 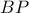 , δηλ. με την ευθεία
, δηλ. με την ευθεία  . Άρα
. Άρα
που σημαίνει ότι
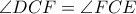 , ή ισοδύναμα ότι η
, ή ισοδύναμα ότι η  διχοτομεί την
διχοτομεί την 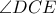 , αφού τα σημεία
, αφού τα σημεία 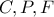 είναι συνευθειακά.
είναι συνευθειακά.Παρατηρούμε, επίσης, ότι τα σημεία
 ,
,  ,
,  , και
, και  ανήκουν στον κύκλο με κέντρο το
ανήκουν στον κύκλο με κέντρο το  κα ακτίνα
κα ακτίνα 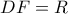 . Επομένως,
. Επομένως,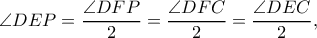
που σημαίνει ότι η
 διχοτομεί την
διχοτομεί την  .
. Αφού η
 διχοτομεί την
διχοτομεί την 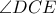 και η
και η  διχοτομεί την
διχοτομεί την  , το
, το  είναι το έγκεντρο του τριγώνου
είναι το έγκεντρο του τριγώνου  .
.Φιλικά,
Αχιλλέας
- Συνημμένα
-
- egmo2020_5_mathematica.png (29.82 KiB) Προβλήθηκε 2655 φορές
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: EGMO 2020
Στο (1) μπορούμε να γράψουμε διάφορες σχετικές προτάσεις που αποδεικνύονται επαγωγικά. Δίνω τη δική μου προσέγγιση αν και δεν είναι η απλούστερη.
Για κάθε φυσικό , αν οι θετικοί ακέραιοι
, αν οι θετικοί ακέραιοι 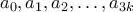 ικανοποιούν τη συνθήκη
ικανοποιούν τη συνθήκη
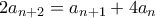 για
για 
τότε για κάθε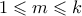 ισχύει ότι
ισχύει ότι 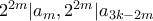 και
και 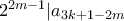 .
.
Θα δείξουμε ότι για κάθε φυσικό , αν οι θετικοί ακέραιοι
, αν οι θετικοί ακέραιοι 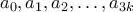 ικανοποιούν τη συνθήκη
ικανοποιούν τη συνθήκη
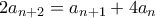 για
για 
τότε για κάθε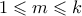 ισχύει ότι
ισχύει ότι 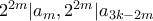 και
και 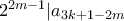 . Αυτό είναι αρκετό αφού τότε για
. Αυτό είναι αρκετό αφού τότε για  (όπως στο πρόβλημα) και
(όπως στο πρόβλημα) και 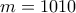 έχουμε
έχουμε 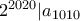 .
.
Για , από τη συνθήκη
, από τη συνθήκη 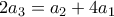 , παίρνουμε
, παίρνουμε 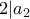 . Τώρα από τη συνθήκη
. Τώρα από τη συνθήκη 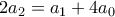 , αφού
, αφού 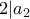 παίρνουμε και
παίρνουμε και  .
.
Άρα ο ισχυρισμός ισχύει για . Ας υποθέσουμε ότι ισχύει για
. Ας υποθέσουμε ότι ισχύει για 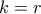 και θα δείξουμε ότι ισχύει και για
και θα δείξουμε ότι ισχύει και για  .
.
Κοιτάζοντας τους όρους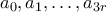 από την επαγωγική υπόθεση παίρνουμε ότι
από την επαγωγική υπόθεση παίρνουμε ότι
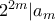 για κάθε
για κάθε 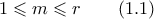
Παίρνουμε επίσης ότι

Κοιτάζοντας τους όρους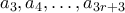 από την επαγωγική υπόθεση παίρνουμε ότι
από την επαγωγική υπόθεση παίρνουμε ότι
 για κάθε
για κάθε 
και
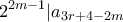 για κάθε
για κάθε 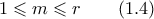
Μένει να δείξουμε ότι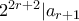 και
και  .
.
Από τη συνθήκη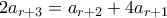 και αφού
και αφού  (από την (1.2)) και
(από την (1.2)) και 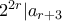 (από την (1.3) με
(από την (1.3) με 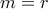 ) τότε
) τότε  .
.
Από τη συνθήκη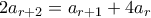 και αφού
και αφού  (από την προηγούμενη παράγραφο) και
(από την προηγούμενη παράγραφο) και  (από την (1.1) για
(από την (1.1) για 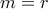 ) παίρνουμε ότι
) παίρνουμε ότι 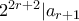 .
.
Οπότε το επαγωγικό βήμα και άρα και η απόδειξη έχει ολοκληρωθεί.
Για κάθε φυσικό
 , αν οι θετικοί ακέραιοι
, αν οι θετικοί ακέραιοι 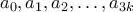 ικανοποιούν τη συνθήκη
ικανοποιούν τη συνθήκη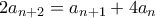 για
για 
τότε για κάθε
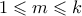 ισχύει ότι
ισχύει ότι 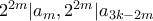 και
και 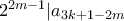 .
.Θα δείξουμε ότι για κάθε φυσικό
 , αν οι θετικοί ακέραιοι
, αν οι θετικοί ακέραιοι 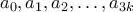 ικανοποιούν τη συνθήκη
ικανοποιούν τη συνθήκη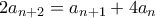 για
για 
τότε για κάθε
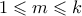 ισχύει ότι
ισχύει ότι 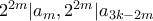 και
και 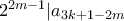 . Αυτό είναι αρκετό αφού τότε για
. Αυτό είναι αρκετό αφού τότε για  (όπως στο πρόβλημα) και
(όπως στο πρόβλημα) και 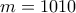 έχουμε
έχουμε 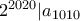 .
.Για
 , από τη συνθήκη
, από τη συνθήκη 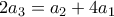 , παίρνουμε
, παίρνουμε 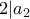 . Τώρα από τη συνθήκη
. Τώρα από τη συνθήκη 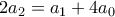 , αφού
, αφού 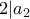 παίρνουμε και
παίρνουμε και  .
.Άρα ο ισχυρισμός ισχύει για
 . Ας υποθέσουμε ότι ισχύει για
. Ας υποθέσουμε ότι ισχύει για 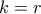 και θα δείξουμε ότι ισχύει και για
και θα δείξουμε ότι ισχύει και για  .
. Κοιτάζοντας τους όρους
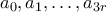 από την επαγωγική υπόθεση παίρνουμε ότι
από την επαγωγική υπόθεση παίρνουμε ότι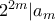 για κάθε
για κάθε 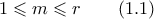
Παίρνουμε επίσης ότι

Κοιτάζοντας τους όρους
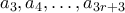 από την επαγωγική υπόθεση παίρνουμε ότι
από την επαγωγική υπόθεση παίρνουμε ότι για κάθε
για κάθε 
και
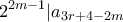 για κάθε
για κάθε 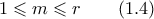
Μένει να δείξουμε ότι
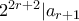 και
και  .
. Από τη συνθήκη
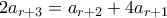 και αφού
και αφού  (από την (1.2)) και
(από την (1.2)) και 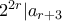 (από την (1.3) με
(από την (1.3) με 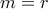 ) τότε
) τότε  .
.Από τη συνθήκη
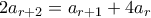 και αφού
και αφού  (από την προηγούμενη παράγραφο) και
(από την προηγούμενη παράγραφο) και  (από την (1.1) για
(από την (1.1) για 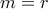 ) παίρνουμε ότι
) παίρνουμε ότι 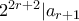 .
.Οπότε το επαγωγικό βήμα και άρα και η απόδειξη έχει ολοκληρωθεί.
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: EGMO 2020
Στο Πρόβλημα 4 είναι σχετικά απλό το 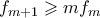 αλλά δεν είχα προσέξει τον τρόπο του Αχιλλέα για να πάρω ακόμη
αλλά δεν είχα προσέξει τον τρόπο του Αχιλλέα για να πάρω ακόμη  φρέσκιες μεταθέσεις. Έτσι βρήκα τελικά αυτήν την απόδειξη:
φρέσκιες μεταθέσεις. Έτσι βρήκα τελικά αυτήν την απόδειξη:
Για κάθε μετάθεση των
των 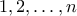 γράφουμε
γράφουμε 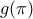 για το ελάχιστο
για το ελάχιστο  ώστε οι πρώτοι
ώστε οι πρώτοι  αριθμοί στη μετάθεση να είναι οι
αριθμοί στη μετάθεση να είναι οι  σε κάποια σειρά. Άρα η
σε κάποια σειρά. Άρα η  είναι φρέσκια αν και μόνο αν
είναι φρέσκια αν και μόνο αν 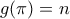 .
.
Παρατηρούμε ότι υπάρχουν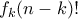 μεταθέσεις
μεταθέσεις  των
των 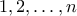 με
με 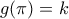 . Πράγματι, αν περιοριστούμε στους πρώτους
. Πράγματι, αν περιοριστούμε στους πρώτους  αριθμούς η μετάθεση που ορίζουν πρέπει να είναι φρέσκια, ενώ στους τελευταίους
αριθμούς η μετάθεση που ορίζουν πρέπει να είναι φρέσκια, ενώ στους τελευταίους  αριθμούς μπορούμε να έχουμε οποιαδήποτε μετάθεση. Επομένως
αριθμούς μπορούμε να έχουμε οποιαδήποτε μετάθεση. Επομένως

Παρατηρούμε τώρα ότι
![\begin{aligned}
0 &= (n+1)! - (n+2)n! + n(n-1)! \\
&= \sum_{k=1}^{n+1} f_k(n+1-k)! - (n+2)\sum_{k=1}^n f_k(n-k)! + n\sum_{k=1}^{n-1} f_k(n-1-k)! \\
&= f_{n+1} - (n+1)f_n + \sum_{k=1}^{n-1} f_k(n-k)![(n-k)(n+1-k)+n-(n+2)(n-k)] \\
&= f_{n+1} - (n+1)f_n + \sum_{k=1}^{n-1} f_k(n-k)![n-(n-k)(k+1)] \\
&= f_{n+1} - (n+1)f_n - \sum_{k=1}^{n-1} f_k(n-k)!k(n-1-k)
\end{aligned} \begin{aligned}
0 &= (n+1)! - (n+2)n! + n(n-1)! \\
&= \sum_{k=1}^{n+1} f_k(n+1-k)! - (n+2)\sum_{k=1}^n f_k(n-k)! + n\sum_{k=1}^{n-1} f_k(n-1-k)! \\
&= f_{n+1} - (n+1)f_n + \sum_{k=1}^{n-1} f_k(n-k)![(n-k)(n+1-k)+n-(n+2)(n-k)] \\
&= f_{n+1} - (n+1)f_n + \sum_{k=1}^{n-1} f_k(n-k)![n-(n-k)(k+1)] \\
&= f_{n+1} - (n+1)f_n - \sum_{k=1}^{n-1} f_k(n-k)!k(n-1-k)
\end{aligned}](/forum/ext/geomar/texintegr/latexrender/pictures/27396a7b269c2103d413cddae5755f1a.png)
Επομένως

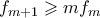 αλλά δεν είχα προσέξει τον τρόπο του Αχιλλέα για να πάρω ακόμη
αλλά δεν είχα προσέξει τον τρόπο του Αχιλλέα για να πάρω ακόμη  φρέσκιες μεταθέσεις. Έτσι βρήκα τελικά αυτήν την απόδειξη:
φρέσκιες μεταθέσεις. Έτσι βρήκα τελικά αυτήν την απόδειξη:Για κάθε μετάθεση
 των
των 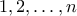 γράφουμε
γράφουμε 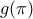 για το ελάχιστο
για το ελάχιστο  ώστε οι πρώτοι
ώστε οι πρώτοι  αριθμοί στη μετάθεση να είναι οι
αριθμοί στη μετάθεση να είναι οι  σε κάποια σειρά. Άρα η
σε κάποια σειρά. Άρα η  είναι φρέσκια αν και μόνο αν
είναι φρέσκια αν και μόνο αν 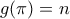 .
. Παρατηρούμε ότι υπάρχουν
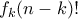 μεταθέσεις
μεταθέσεις  των
των 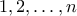 με
με 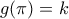 . Πράγματι, αν περιοριστούμε στους πρώτους
. Πράγματι, αν περιοριστούμε στους πρώτους  αριθμούς η μετάθεση που ορίζουν πρέπει να είναι φρέσκια, ενώ στους τελευταίους
αριθμούς η μετάθεση που ορίζουν πρέπει να είναι φρέσκια, ενώ στους τελευταίους  αριθμούς μπορούμε να έχουμε οποιαδήποτε μετάθεση. Επομένως
αριθμούς μπορούμε να έχουμε οποιαδήποτε μετάθεση. Επομένως
Παρατηρούμε τώρα ότι
![\begin{aligned}
0 &= (n+1)! - (n+2)n! + n(n-1)! \\
&= \sum_{k=1}^{n+1} f_k(n+1-k)! - (n+2)\sum_{k=1}^n f_k(n-k)! + n\sum_{k=1}^{n-1} f_k(n-1-k)! \\
&= f_{n+1} - (n+1)f_n + \sum_{k=1}^{n-1} f_k(n-k)![(n-k)(n+1-k)+n-(n+2)(n-k)] \\
&= f_{n+1} - (n+1)f_n + \sum_{k=1}^{n-1} f_k(n-k)![n-(n-k)(k+1)] \\
&= f_{n+1} - (n+1)f_n - \sum_{k=1}^{n-1} f_k(n-k)!k(n-1-k)
\end{aligned} \begin{aligned}
0 &= (n+1)! - (n+2)n! + n(n-1)! \\
&= \sum_{k=1}^{n+1} f_k(n+1-k)! - (n+2)\sum_{k=1}^n f_k(n-k)! + n\sum_{k=1}^{n-1} f_k(n-1-k)! \\
&= f_{n+1} - (n+1)f_n + \sum_{k=1}^{n-1} f_k(n-k)![(n-k)(n+1-k)+n-(n+2)(n-k)] \\
&= f_{n+1} - (n+1)f_n + \sum_{k=1}^{n-1} f_k(n-k)![n-(n-k)(k+1)] \\
&= f_{n+1} - (n+1)f_n - \sum_{k=1}^{n-1} f_k(n-k)!k(n-1-k)
\end{aligned}](/forum/ext/geomar/texintegr/latexrender/pictures/27396a7b269c2103d413cddae5755f1a.png)
Επομένως

- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: EGMO 2020
Δίνω και την προσέγγισή μου στο Πρόβλημα 5. Η λύση μου ήταν με κάπως διαφορετική σειρά από όπως την έγραψα εδώ. Πρώτα με κυνήγι γωνιών έφτασα στο γεγονός ότι αρκεί να δείξω ότι 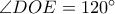 και μετά είδα ότι όντως αυτό ισχύει.
και μετά είδα ότι όντως αυτό ισχύει.
[Οι λύσεις μου στα 2 και 6 θα μπουν αργότερα. Στο 3 δεν βρήκα λύση αλλά αν δεν μπει κάτι θα δώσω μια από τις επίσημες.]
αλλά αν δεν μπει κάτι θα δώσω μια από τις επίσημες.]
Έστω το κέντρο του
το κέντρο του  και έστω ότι έχει συντεταγμένες
και έστω ότι έχει συντεταγμένες  . Μπορούμε να υποθέσουμε ότι
. Μπορούμε να υποθέσουμε ότι 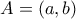 και
και 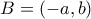 . Τότε
. Τότε 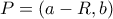 . Αν
. Αν  το σημείο τομής της
το σημείο τομής της  με την
με την  τότε
τότε  το μέσο της
το μέσο της  , επομένως
, επομένως 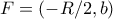 . Η εξίσωση της
. Η εξίσωση της  είναι η
είναι η  επομένως η εξίσωση της
επομένως η εξίσωση της  που είναι κάθετη στην
που είναι κάθετη στην  και περνά από το
και περνά από το  είναι η
είναι η  . Από τριγωνομετρία βγαίνει τώρα ότι
. Από τριγωνομετρία βγαίνει τώρα ότι 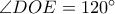 .
.
Έχουμε λοιπόν και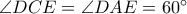 . Έστω
. Έστω 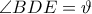 . Τότε έχουμε
. Τότε έχουμε 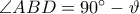 και
και 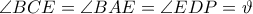 . Επίσης,
. Επίσης, 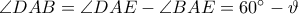 .
.
Έστω . Αφού
. Αφού  έχουμε
έχουμε  και άρα
και άρα 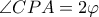 . Είναι όμως και
. Είναι όμως και 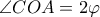 , επομένως τα
, επομένως τα 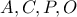 είναι ομοκυκλικά.
είναι ομοκυκλικά.
Είναι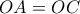 οπότε
οπότε  . Από ομοκυκλικότητα είναι και
. Από ομοκυκλικότητα είναι και  . Όμως
. Όμως 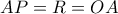 . Άρα
. Άρα  από όπου λαμβάνουμε
από όπου λαμβάνουμε  .
.
Τότε παίρνουμε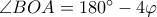 οπότε
οπότε  . Ξέρουμε επίσης ότι
. Ξέρουμε επίσης ότι

Από τις δύο αυτές σχέσεις παίρνουμε .
.
Τότε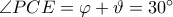 και αφού
και αφού  ή
ή 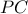 διχοτομεί την
διχοτομεί την 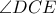 . Επίσης
. Επίσης

Δηλαδή η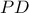 διχοτομεί την
διχοτομεί την  .
.
Επομένως όντως έχουμε ότι το είναι το έγκεντρο του τριγώνου
είναι το έγκεντρο του τριγώνου  .
.
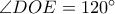 και μετά είδα ότι όντως αυτό ισχύει.
και μετά είδα ότι όντως αυτό ισχύει.[Οι λύσεις μου στα 2 και 6 θα μπουν αργότερα. Στο 3 δεν βρήκα λύση
Έστω
 το κέντρο του
το κέντρο του  και έστω ότι έχει συντεταγμένες
και έστω ότι έχει συντεταγμένες  . Μπορούμε να υποθέσουμε ότι
. Μπορούμε να υποθέσουμε ότι 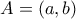 και
και 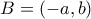 . Τότε
. Τότε 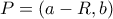 . Αν
. Αν  το σημείο τομής της
το σημείο τομής της  με την
με την  τότε
τότε  το μέσο της
το μέσο της  , επομένως
, επομένως 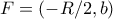 . Η εξίσωση της
. Η εξίσωση της  είναι η
είναι η  επομένως η εξίσωση της
επομένως η εξίσωση της  που είναι κάθετη στην
που είναι κάθετη στην  και περνά από το
και περνά από το  είναι η
είναι η  . Από τριγωνομετρία βγαίνει τώρα ότι
. Από τριγωνομετρία βγαίνει τώρα ότι 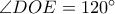 .
.Έχουμε λοιπόν και
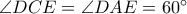 . Έστω
. Έστω 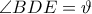 . Τότε έχουμε
. Τότε έχουμε 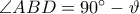 και
και 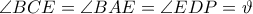 . Επίσης,
. Επίσης, 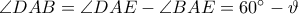 .
.Έστω
 . Αφού
. Αφού  έχουμε
έχουμε  και άρα
και άρα 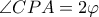 . Είναι όμως και
. Είναι όμως και 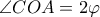 , επομένως τα
, επομένως τα 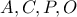 είναι ομοκυκλικά.
είναι ομοκυκλικά. Είναι
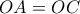 οπότε
οπότε  . Από ομοκυκλικότητα είναι και
. Από ομοκυκλικότητα είναι και  . Όμως
. Όμως 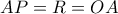 . Άρα
. Άρα  από όπου λαμβάνουμε
από όπου λαμβάνουμε  .
. Τότε παίρνουμε
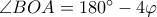 οπότε
οπότε  . Ξέρουμε επίσης ότι
. Ξέρουμε επίσης ότι 
Από τις δύο αυτές σχέσεις παίρνουμε
 .
. Τότε
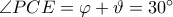 και αφού
και αφού  ή
ή 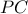 διχοτομεί την
διχοτομεί την 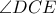 . Επίσης
. Επίσης 
Δηλαδή η
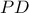 διχοτομεί την
διχοτομεί την  .
. Επομένως όντως έχουμε ότι το
 είναι το έγκεντρο του τριγώνου
είναι το έγκεντρο του τριγώνου  .
.- Διονύσιος Αδαμόπουλος
- Δημοσιεύσεις: 807
- Εγγραφή: Σάβ Μαρ 19, 2016 5:11 pm
- Τοποθεσία: Πύργος Ηλείας
Re: EGMO 2020
Βασικά θα την κατεβάσω, νομίζω έχει ένα κενό σε κάποιο σημείο. Δεν είδατε τίποτα! 
τελευταία επεξεργασία από Διονύσιος Αδαμόπουλος σε Κυρ Απρ 19, 2020 8:30 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Houston, we have a problem!
Re: EGMO 2020
Για την 3.
Αν προεκτείνουμε τις πλευρές του εξαγώνου,φτιάχνουμε τα ισόπλευρα (πρώτη συνθήκη)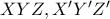 -
- -ωρολογιακά,
-ωρολογιακά, .
.
Από τη δεύτερη συνθήκη,το σημείο τομής των διχοτόμων (έστω ) έχει ίδιες τριγραμμικές ως προς τα
) έχει ίδιες τριγραμμικές ως προς τα  τρίγωνα,και επειδή σε ισόπλευρα τριγραμμικές/βαρυκεντρικές ταυτίζονται,θα έχει και ίδιες βαρυκεντρικές.Οι βαρυκεντρικές είναι "αφινικό αναλλοίωτο" οπότε
τρίγωνα,και επειδή σε ισόπλευρα τριγραμμικές/βαρυκεντρικές ταυτίζονται,θα έχει και ίδιες βαρυκεντρικές.Οι βαρυκεντρικές είναι "αφινικό αναλλοίωτο" οπότε 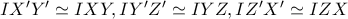 .Μάλιστα,επειδή τα αντίστοιχα ύψη των ομοίων τριγώνων είναι ίσα,θα είναι ίσα και τα
.Μάλιστα,επειδή τα αντίστοιχα ύψη των ομοίων τριγώνων είναι ίσα,θα είναι ίσα και τα  .
.
Αν ορίσουμε ως το σημείο που προκύπτει από το θ.Miquel στο
το σημείο που προκύπτει από το θ.Miquel στο 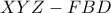 τότε πάλι από Σπειροειδή ομοιότητα θα ισχύει πως το
τότε πάλι από Σπειροειδή ομοιότητα θα ισχύει πως το  θα έχει τις ίδιες βαρυκεντρικές ως προς τα
θα έχει τις ίδιες βαρυκεντρικές ως προς τα  .Άρα θα έχει και τις ίδιες τριγραμμικές και επειδή τα
.Άρα θα έχει και τις ίδιες τριγραμμικές και επειδή τα  είναι ίσα,θα είναι το σημείο τομής των διχοτόμων των
είναι ίσα,θα είναι το σημείο τομής των διχοτόμων των 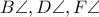 κλπ.
κλπ.
Υγ.Το παραπάνω μπορεί να γραφεί με πολλούς τρόπους-κάποιους καλύτερους,κάποιους χειρότερους (βλ.Aops)
Αν προεκτείνουμε τις πλευρές του εξαγώνου,φτιάχνουμε τα ισόπλευρα (πρώτη συνθήκη)
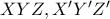 -
- -ωρολογιακά,
-ωρολογιακά, .
.Από τη δεύτερη συνθήκη,το σημείο τομής των διχοτόμων (έστω
 ) έχει ίδιες τριγραμμικές ως προς τα
) έχει ίδιες τριγραμμικές ως προς τα  τρίγωνα,και επειδή σε ισόπλευρα τριγραμμικές/βαρυκεντρικές ταυτίζονται,θα έχει και ίδιες βαρυκεντρικές.Οι βαρυκεντρικές είναι "αφινικό αναλλοίωτο" οπότε
τρίγωνα,και επειδή σε ισόπλευρα τριγραμμικές/βαρυκεντρικές ταυτίζονται,θα έχει και ίδιες βαρυκεντρικές.Οι βαρυκεντρικές είναι "αφινικό αναλλοίωτο" οπότε 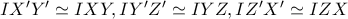 .Μάλιστα,επειδή τα αντίστοιχα ύψη των ομοίων τριγώνων είναι ίσα,θα είναι ίσα και τα
.Μάλιστα,επειδή τα αντίστοιχα ύψη των ομοίων τριγώνων είναι ίσα,θα είναι ίσα και τα  .
.Αν ορίσουμε ως
 το σημείο που προκύπτει από το θ.Miquel στο
το σημείο που προκύπτει από το θ.Miquel στο 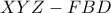 τότε πάλι από Σπειροειδή ομοιότητα θα ισχύει πως το
τότε πάλι από Σπειροειδή ομοιότητα θα ισχύει πως το  θα έχει τις ίδιες βαρυκεντρικές ως προς τα
θα έχει τις ίδιες βαρυκεντρικές ως προς τα  .Άρα θα έχει και τις ίδιες τριγραμμικές και επειδή τα
.Άρα θα έχει και τις ίδιες τριγραμμικές και επειδή τα  είναι ίσα,θα είναι το σημείο τομής των διχοτόμων των
είναι ίσα,θα είναι το σημείο τομής των διχοτόμων των 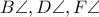 κλπ.
κλπ.Υγ.Το παραπάνω μπορεί να γραφεί με πολλούς τρόπους-κάποιους καλύτερους,κάποιους χειρότερους (βλ.Aops)
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: EGMO 2020
Βάζω τη λύση μου στο (2). Από ότι βλέπω αποδείχθηκε αρκετά δύσκολη αν και ουσιαστικά δεν χρησιμοποιεί κάποια δύσκολη ανισότητα.
Λήμμα: Αν μη αρνητικοί πραγματικοί αριθμοί με
μη αρνητικοί πραγματικοί αριθμοί με  τότε
τότε
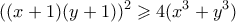
με ισότητα αν και μόνο αν ή
ή  .
.
Απόδειξη Λήμματος: Έχουμε
![\begin{aligned}
(x+1)^2(y+1)^2 - (x-1)^2(y-1)^2 &= (xy+x+y-1)^2 - (xy-x-y+1)^2 \\
&= 4(x+y)(xy+1) \\
&\geqslant 4(x+y)[xy + (y-x)^2] \\
&= 4(x+y)(x^2-xy + y^2) \\
&= 4(x^3 + y^3)
\end{aligned} \begin{aligned}
(x+1)^2(y+1)^2 - (x-1)^2(y-1)^2 &= (xy+x+y-1)^2 - (xy-x-y+1)^2 \\
&= 4(x+y)(xy+1) \\
&\geqslant 4(x+y)[xy + (y-x)^2] \\
&= 4(x+y)(x^2-xy + y^2) \\
&= 4(x^3 + y^3)
\end{aligned}](/forum/ext/geomar/texintegr/latexrender/pictures/05570198957535323c370a9ea6064735.png)
Άρα η ανισότητα έχει αποδειχθεί. Επιπλέον η ισότητα ισχύει αν και μόνο αν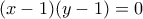 και
και 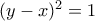 από όπου προκύπτει ο ισχυρισμός.
από όπου προκύπτει ο ισχυρισμός. 
Στο πρόβλημα τώρα, για οποιαδήποτε μετάθεση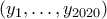 της
της 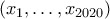 παίρνουμε
παίρνουμε
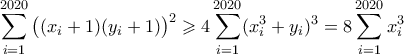
Για την ισότητα πρέπει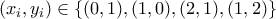 για κάθε
για κάθε  .
.
Από τις συνθήκες (i) και (ii) πρέπει απαραίτητα η λίστα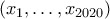 να απότελείται μόνο από
να απότελείται μόνο από  και
και  ή μόνο από
ή μόνο από  και
και  .
.
Αν αποτελείται μόνο από και
και  τότε πρέπει να έχουμε από ίσο αριθμό, αλλιώς από την αρχή του περιστερώνα θα υπάρχει
τότε πρέπει να έχουμε από ίσο αριθμό, αλλιώς από την αρχή του περιστερώνα θα υπάρχει  ώστε
ώστε 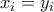 . Ομοίως και αν αποτελείται από μόνο
. Ομοίως και αν αποτελείται από μόνο  και
και  .
.
Άρα οι μόνες λίστες που ικανοποιούν τις συνθήκες είναι οι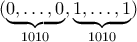 και
και 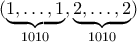
Λήμμα: Αν
 μη αρνητικοί πραγματικοί αριθμοί με
μη αρνητικοί πραγματικοί αριθμοί με  τότε
τότε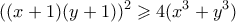
με ισότητα αν και μόνο αν
 ή
ή  .
.Απόδειξη Λήμματος: Έχουμε
![\begin{aligned}
(x+1)^2(y+1)^2 - (x-1)^2(y-1)^2 &= (xy+x+y-1)^2 - (xy-x-y+1)^2 \\
&= 4(x+y)(xy+1) \\
&\geqslant 4(x+y)[xy + (y-x)^2] \\
&= 4(x+y)(x^2-xy + y^2) \\
&= 4(x^3 + y^3)
\end{aligned} \begin{aligned}
(x+1)^2(y+1)^2 - (x-1)^2(y-1)^2 &= (xy+x+y-1)^2 - (xy-x-y+1)^2 \\
&= 4(x+y)(xy+1) \\
&\geqslant 4(x+y)[xy + (y-x)^2] \\
&= 4(x+y)(x^2-xy + y^2) \\
&= 4(x^3 + y^3)
\end{aligned}](/forum/ext/geomar/texintegr/latexrender/pictures/05570198957535323c370a9ea6064735.png)
Άρα η ανισότητα έχει αποδειχθεί. Επιπλέον η ισότητα ισχύει αν και μόνο αν
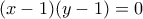 και
και 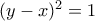 από όπου προκύπτει ο ισχυρισμός.
από όπου προκύπτει ο ισχυρισμός. 
Στο πρόβλημα τώρα, για οποιαδήποτε μετάθεση
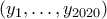 της
της 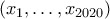 παίρνουμε
παίρνουμε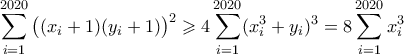
Για την ισότητα πρέπει
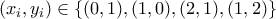 για κάθε
για κάθε  .
.Από τις συνθήκες (i) και (ii) πρέπει απαραίτητα η λίστα
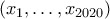 να απότελείται μόνο από
να απότελείται μόνο από  και
και  ή μόνο από
ή μόνο από  και
και  .
. Αν αποτελείται μόνο από
 και
και  τότε πρέπει να έχουμε από ίσο αριθμό, αλλιώς από την αρχή του περιστερώνα θα υπάρχει
τότε πρέπει να έχουμε από ίσο αριθμό, αλλιώς από την αρχή του περιστερώνα θα υπάρχει  ώστε
ώστε 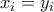 . Ομοίως και αν αποτελείται από μόνο
. Ομοίως και αν αποτελείται από μόνο  και
και  .
.Άρα οι μόνες λίστες που ικανοποιούν τις συνθήκες είναι οι
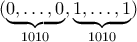 και
και 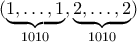
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: EGMO 2020
Βάζω τη λύση μου για αυτό. Για ώρα παιδευόμουν με γενικευμένη Pell. Εν τέλει κλειδί της λύσης ήταν να κοιτάξω την ακολουθία modulo
 για συγκεκριμένο
για συγκεκριμένο  .
.Αν
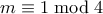 τότε modulo
τότε modulo  η ακολουθία γίνεται
η ακολουθία γίνεται 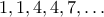 , άτοπο αφού το
, άτοπο αφού το  δεν είναι τέλειο τετράγωνο modulo
δεν είναι τέλειο τετράγωνο modulo  .
.Αν
 τότε modulo
τότε modulo  η ακολουθία γίνεται
η ακολουθία γίνεται 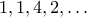 , άτοπο αφού το
, άτοπο αφού το  δεν είναι τέλειο τετράγωνο modulo
δεν είναι τέλειο τετράγωνο modulo  .
.Επομένως ο
 είναι άρτιος. Έστω
είναι άρτιος. Έστω  πρώτος ώστε
πρώτος ώστε 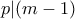 . Πρέπει
. Πρέπει  περιττός. Modulo
περιττός. Modulo  έχουμε
έχουμε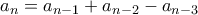
για κάθε
 . Επειδή
. Επειδή 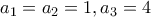 είναι απλό να ελεγχθεί επαγωγικά ότι
είναι απλό να ελεγχθεί επαγωγικά ότι 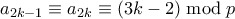 .
.Αν
 , τότε από το Κινέζικο Θεώρημα η ακολουθία
, τότε από το Κινέζικο Θεώρημα η ακολουθία  παίρνει όλες τις τιμές modulo
παίρνει όλες τις τιμές modulo  . Άρα όλες οι τιμές modulo
. Άρα όλες οι τιμές modulo  είναι τέλεια τετράγωνα modulo
είναι τέλεια τετράγωνα modulo  , άτοπο αφού ως γνωστό υπάρχει
, άτοπο αφού ως γνωστό υπάρχει  τετραγωνικά μη υπόλοιπα modulo
τετραγωνικά μη υπόλοιπα modulo  .
.Άρα πρέπει
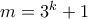 για κάποιο μη αρνητικό ακέραιο
για κάποιο μη αρνητικό ακέραιο  . Επίσης, αφού
. Επίσης, αφού 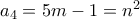 , για κάποιο φυσικό
, για κάποιο φυσικό  , πρέπει
, πρέπει 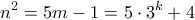
Παίρνουμε
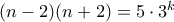 και αφού
και αφού 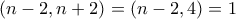 . (Οι μόνοι πιθανοί διαιρέτες των
. (Οι μόνοι πιθανοί διαιρέτες των  και
και  είναι τα
είναι τα  και
και  .)
.)Άρα
 και
και  ή
ή 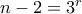 και
και 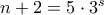 για κάποιους φυσικούς
για κάποιους φυσικούς  με
με 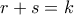 .
. Στην πρώτη περίπτωση παίρνουμε
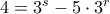 . Πρέπει
. Πρέπει  ή
ή  και εύκολα βλέπουμε ότι η μόνη λύση είναι η
και εύκολα βλέπουμε ότι η μόνη λύση είναι η  που δίνει
που δίνει  και
και 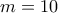 .
. Στη δεύτερη περίπτωση παίρνουμε
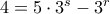 . Πρέπει
. Πρέπει  ή
ή  και εύκολα βλέπουμε ότι η μόνη λύση είναι η
και εύκολα βλέπουμε ότι η μόνη λύση είναι η 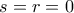 που δίνει
που δίνει  και
και  .
.Επομένως οι μόνες πιθανές περιπτώσεις είναι
 ή
ή 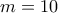 . Αν
. Αν  παρατηρούμε ότι η ακολουθία είναι η
παρατηρούμε ότι η ακολουθία είναι η 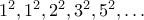 . Αρκεί λοιπόν να δείξουμε ότι
. Αρκεί λοιπόν να δείξουμε ότι 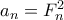 . Το ζητούμενο ισχύει για
. Το ζητούμενο ισχύει για  . Έστω ότι ισχύει για
. Έστω ότι ισχύει για 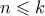 . Για
. Για 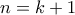 έχουμε
έχουμε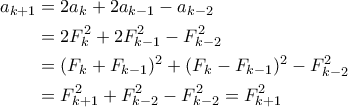
Άρα επαγωγικά έχουμε
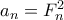 για κάθε φυσικό
για κάθε φυσικό  .
.Αν
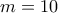 παρατηρούμε ότι η ακολουθία είναι η
παρατηρούμε ότι η ακολουθία είναι η 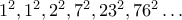 . Ορίζουμε την ακολουθία
. Ορίζουμε την ακολουθία  με
με 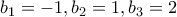 και αναδρομικό τύπο
και αναδρομικό τύπο 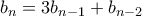 για
για  . (Προσοχή στην τιμή του
. (Προσοχή στην τιμή του  .) Αρκεί να δείξουμε ότι
.) Αρκεί να δείξουμε ότι 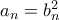 το οποίο ισχύει για
το οποίο ισχύει για  . Για
. Για  έχουμε
έχουμε 
Άρα επαγωγικά έχουμε
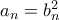 για κάθε φυσικό
για κάθε φυσικό  .
.Επομένως οι μόνες δυνατές τιμές του
 είναι οι
είναι οι  και
και 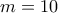 .
.Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 31 επισκέπτες
