Σελίδα 1 από 1
Τεστ Εξάσκησης (15), Μεγάλοι
Δημοσιεύτηκε: Παρ Απρ 10, 2020 2:41 am
από socrates
ΘΕΜΑ 1
Έστω μία συνάρτηση

Να δείξετε, ότι οι πιο κάτω συνθήκες είναι ισοδύναμες:
 και
και 
Bonus: Βρείτε όλες τις συναρτήσεις

για τις οποίες
 ΘΕΜΑ 2
ΘΕΜΑ 2
Για όλους τους θετικούς ακεραίους

να δείξετε ότι:
 ΘΕΜΑ 3
ΘΕΜΑ 3
Θεωρούμε οξυγώνιο τρίγωνο

με

. Τα σημεία

και

είναι τα ίχνη των υψών από τις κορυφές

και

, αντίστοιχα. Η ευθεία που εφάπτεται στον περιγεγραμμένο κύκλο του τριγώνου

στο

τέμνει την

στο

. Η ευθεία που είναι παράλληλη στην

και διέρχεται από το

τέμνει την

στο

. Να αποδείξετε ότι η

είναι κάθετη στη διάμεσο από το

του τριγώνου

.
ΘΕΜΑ 4
Προσδιορίστε αν είναι δυνατό να διατάξουμε τους αριθμούς

έτσι ώστε να υπάρχουν

αριθμοί μεταξύ δύο

, όταν
i)

ii)

iii)

(Για παράδειγμα, για

,

είναι μια τέτοια διάταξη.)
To πρόβλημα 1 είναι κατασκευασμένο από τον
Ορέστη.
Τα θέματα 2 και 4 προτείνει ο
ksofsa.
Re: Τεστ Εξάσκησης (15), Μεγάλοι
Δημοσιεύτηκε: Παρ Απρ 10, 2020 11:37 am
από miltosk
socrates έγραψε: ↑Παρ Απρ 10, 2020 2:41 am
ΘΕΜΑ 1
Έστω μία συνάρτηση

Να δείξετε, ότι οι πιο κάτω συνθήκες είναι ισοδύναμες:
 και
και 
Bonus: Βρείτε όλες τις συναρτήσεις

για τις οποίες



και η f 1-1.
Θέτω

και λαμβάνω ότι

τέτοιο ώστε

(δεν το ρισκάρω με το επί του

)
Για

λαμβάνω

Για
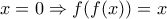
Άρα η (1) γίνεται


:

Άρα από την (1) κατέληξα στα:

Το αντίστροφο:

Θέτω
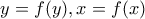
και:

που είναι η (1).
Τελικά, οι σχέσεις είναι ισοδύναμες.
Για το Bonus:
Εναλλάσοντας τους ρόλους των

καταλήγω στην:

Θέτω

και έχω

δηλαδή

σταθερή.
Άρα

Άρα f:1-1 και θέτω στην αρχική

(edit: διορθώθηκε μετά από ΠΜ του κ. Θανάση)
και λαμβάνω ότι

Για

στην αρχική έχω:

Άρα

Άρα

Η αρχική γίνεται:

Για

:

Δηλαδή άγεται σε Cauchy.
Μπορώ να τελειώσω με 2 τρόπους:
Είτε αφού

για

,

και από την

παίρνω

Είτε:

δηλαδή f γνησίως αύξουσα και καταλήγω με

Άρα

.
Re: Τεστ Εξάσκησης (15), Μεγάλοι
Δημοσιεύτηκε: Παρ Απρ 10, 2020 11:50 am
από miltosk
socrates έγραψε: ↑Παρ Απρ 10, 2020 2:41 am
ΘΕΜΑ 2
Για όλους τους θετικούς ακεραίους

να δείξετε ότι:


Έστω

.
Τότε:

και

Άρα


και αφού

Τώρα:
![[m,n]=\frac{mn}{(m,n)}=\frac{mn}{d_1} [m,n]=\frac{mn}{(m,n)}=\frac{mn}{d_1}](/forum/ext/geomar/texintegr/latexrender/pictures/29c9af1f24e76117b39f9b4073f628c4.png)
![[m+1,n+1]=\frac{(m+1)(n+1)}
{(m+1,n+1)}=\frac{mn+m+n+1}{d_2}>\frac{mn}{d_2} [m+1,n+1]=\frac{(m+1)(n+1)}
{(m+1,n+1)}=\frac{mn+m+n+1}{d_2}>\frac{mn}{d_2}](/forum/ext/geomar/texintegr/latexrender/pictures/907794b8b2c49b966f0d10f904300521.png)
Άρα
![[m,n]+[m+1,n+1]>mn(\frac{1}{d_1}+\frac{1}{d_2})\geq mn\cdot2\frac{1}{\sqrt{d_1d_2}}\geq\frac{2mn}{\sqrt{m-n}} [m,n]+[m+1,n+1]>mn(\frac{1}{d_1}+\frac{1}{d_2})\geq mn\cdot2\frac{1}{\sqrt{d_1d_2}}\geq\frac{2mn}{\sqrt{m-n}}](/forum/ext/geomar/texintegr/latexrender/pictures/6e99caa3dbc36eaf8dc6f759114cf442.png)
Re: Τεστ Εξάσκησης (15), Μεγάλοι
Δημοσιεύτηκε: Παρ Απρ 10, 2020 11:52 am
από ΦΩΤΙΑΔΗΣ ΠΡΟΔΡΟΜΟΣ
socrates έγραψε: ↑Παρ Απρ 10, 2020 2:41 am
ΘΕΜΑ 1
Έστω μία συνάρτηση

Να δείξετε, ότι οι πιο κάτω συνθήκες είναι ισοδύναμες:
 και
και 
Ευθύ:
Με

σταθερό αλλάζοντας το

εύκολα η

είναι

Με

παίρνω

δηλαδή

.
Με

παίρνω

.
Αυτή για

δίνει

.Η αρχική για
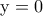
δίνει

.
Άρα

Το ανάποδο:

και η απόδειξη ολοκληρώθηκε.
Re: Τεστ Εξάσκησης (15), Μεγάλοι
Δημοσιεύτηκε: Παρ Απρ 10, 2020 12:00 pm
από miltosk
socrates έγραψε: ↑Παρ Απρ 10, 2020 2:41 am
ΘΕΜΑ 3
Θεωρούμε οξυγώνιο τρίγωνο

με

. Τα σημεία

και

είναι τα ίχνη των υψών από τις κορυφές

και

, αντίστοιχα. Η ευθεία που εφάπτεται στον περιγεγραμμένο κύκλο του τριγώνου

στο

τέμνει την

στο

. Η ευθεία που είναι παράλληλη στην

και διέρχεται από το

τέμνει την

στο

. Να αποδείξετε ότι η

είναι κάθετη στη διάμεσο από το

του τριγώνου

Μιας και πήρα φόρα:
Ας είναι

η τομή των

,

.

εγγράψιμο με κέντρο κύκλου το μέσο

της

.
Τότε

πολική του

και άρα

μεταξύ τους κάθετες.
Αρκεί

Από το πλήρες τετράπλευρο

η δέσμη

είναι αρμονική. Έτσι, αν η

τέμνει την

στο

,

μέσο της

.
Από θεώρημα Nagel,

παραλληλόγραμμο.
Άρα

.
Άρα

παραλληλόγραμμο και το ζητούμενο έπεται.
Re: Τεστ Εξάσκησης (15), Μεγάλοι
Δημοσιεύτηκε: Πέμ Ιούλ 02, 2020 10:06 pm
από stamas1
miltosk έγραψε: ↑Παρ Απρ 10, 2020 12:00 pm
socrates έγραψε: ↑Παρ Απρ 10, 2020 2:41 am
ΘΕΜΑ 3
Θεωρούμε οξυγώνιο τρίγωνο

με

. Τα σημεία

και

είναι τα ίχνη των υψών από τις κορυφές

και

, αντίστοιχα. Η ευθεία που εφάπτεται στον περιγεγραμμένο κύκλο του τριγώνου

στο

τέμνει την

στο

. Η ευθεία που είναι παράλληλη στην

και διέρχεται από το

τέμνει την

στο

. Να αποδείξετε ότι η

είναι κάθετη στη διάμεσο από το

του τριγώνου

Μιας και πήρα φόρα:
Ας είναι

η τομή των

,

.

εγγράψιμο με κέντρο κύκλου το μέσο

της

.
Τότε

πολική του

και άρα

μεταξύ τους κάθετες.
Αρκεί

Από το πλήρες τετράπλευρο

η δέσμη

είναι αρμονική. Έτσι, αν η

τέμνει την

στο

,

μέσο της

.
Από θεώρημα Nagel,

παραλληλόγραμμο.
Άρα

.
Άρα

παραλληλόγραμμο και το ζητούμενο έπεται.
Το σημειο Η που ακριβως ειναι?(το ορθοκεντρο?)
Re: Τεστ Εξάσκησης (15), Μεγάλοι
Δημοσιεύτηκε: Παρ Ιούλ 03, 2020 12:58 am
από miltosk
stamas1 έγραψε: ↑Πέμ Ιούλ 02, 2020 10:06 pm
miltosk έγραψε: ↑Παρ Απρ 10, 2020 12:00 pm
socrates έγραψε: ↑Παρ Απρ 10, 2020 2:41 am
ΘΕΜΑ 3
Θεωρούμε οξυγώνιο τρίγωνο

με

. Τα σημεία

και

είναι τα ίχνη των υψών από τις κορυφές

και

, αντίστοιχα. Η ευθεία που εφάπτεται στον περιγεγραμμένο κύκλο του τριγώνου

στο

τέμνει την

στο

. Η ευθεία που είναι παράλληλη στην

και διέρχεται από το

τέμνει την

στο

. Να αποδείξετε ότι η

είναι κάθετη στη διάμεσο από το

του τριγώνου

Μιας και πήρα φόρα:
Ας είναι

η τομή των

,

.

εγγράψιμο με κέντρο κύκλου το μέσο

της

.
Τότε

πολική του

και άρα

μεταξύ τους κάθετες.
Αρκεί

Από το πλήρες τετράπλευρο

η δέσμη

είναι αρμονική. Έτσι, αν η

τέμνει την

στο

,

μέσο της

.
Από θεώρημα Nagel,

παραλληλόγραμμο.
Άρα

.
Άρα

παραλληλόγραμμο και το ζητούμενο έπεται.
Το σημειο Η που ακριβως ειναι?(το ορθοκεντρο?)
Ναι το ορθόκεντρο του

είναι, το ξέχασα από κεκτημένη ταχύτητα.
Re: Τεστ Εξάσκησης (15), Μεγάλοι
Δημοσιεύτηκε: Τετ Φεβ 17, 2021 9:58 am
από Demetres
Philip.kal έγραψε: ↑Τετ Φεβ 17, 2021 8:06 am
socrates έγραψε: ↑Παρ Απρ 10, 2020 2:41 am
ΘΕΜΑ 2
Για όλους τους θετικούς ακεραίους

να δείξετε ότι:

Μία διαφορετική για το 2. Είναι:
![\left [ m,n \right ]\leqslant mn, \left [ m+1,n+1 \right ]\leqslant (m+1)(n+1) \left [ m,n \right ]\leqslant mn, \left [ m+1,n+1 \right ]\leqslant (m+1)(n+1)](/forum/ext/geomar/texintegr/latexrender/pictures/7a198417c5db4c431c48ed044cfc8097.png)
. Πρέπει, συνεπώς, να ισχύει ισοδύναμα:

.
Η τελευταία προφανώς ισχύει.
Προσοχή. Δεν είναι σωστό αυτό. Ουσιαστικά λές
![\displaystyle [m,n] + [m+1,n+1] \leqslant mn + (m+1)(n+1) \geqslant \frac{2mn}{\sqrt{m-n}} \displaystyle [m,n] + [m+1,n+1] \leqslant mn + (m+1)(n+1) \geqslant \frac{2mn}{\sqrt{m-n}}](/forum/ext/geomar/texintegr/latexrender/pictures/03ff5e3a517c9c26c2002f7e82e594cb.png)
Re: Τεστ Εξάσκησης (15), Μεγάλοι
Δημοσιεύτηκε: Τετ Φεβ 17, 2021 1:08 pm
από Demetres
Έβαλα μια λύση για το 4
εδώ.
 Να δείξετε, ότι οι πιο κάτω συνθήκες είναι ισοδύναμες:
Να δείξετε, ότι οι πιο κάτω συνθήκες είναι ισοδύναμες:
 για τις οποίες
για τις οποίες 
 να δείξετε ότι:
να δείξετε ότι:
 με
με  . Τα σημεία
. Τα σημεία  και
και  είναι τα ίχνη των υψών από τις κορυφές
είναι τα ίχνη των υψών από τις κορυφές  και
και  , αντίστοιχα. Η ευθεία που εφάπτεται στον περιγεγραμμένο κύκλο του τριγώνου
, αντίστοιχα. Η ευθεία που εφάπτεται στον περιγεγραμμένο κύκλο του τριγώνου  στο
στο  τέμνει την
τέμνει την  στο
στο  . Η ευθεία που είναι παράλληλη στην
. Η ευθεία που είναι παράλληλη στην  και διέρχεται από το
και διέρχεται από το  τέμνει την
τέμνει την  στο
στο  . Να αποδείξετε ότι η
. Να αποδείξετε ότι η  είναι κάθετη στη διάμεσο από το
είναι κάθετη στη διάμεσο από το  του τριγώνου
του τριγώνου  .
. έτσι ώστε να υπάρχουν
έτσι ώστε να υπάρχουν  αριθμοί μεταξύ δύο
αριθμοί μεταξύ δύο  , όταν
, όταν


 ,
,  είναι μια τέτοια διάταξη.)
είναι μια τέτοια διάταξη.) Να δείξετε, ότι οι πιο κάτω συνθήκες είναι ισοδύναμες:
Να δείξετε, ότι οι πιο κάτω συνθήκες είναι ισοδύναμες:
 και
και 
 για τις οποίες
για τις οποίες 
 να δείξετε ότι:
να δείξετε ότι:
 με
με  . Τα σημεία
. Τα σημεία  και
και  είναι τα ίχνη των υψών από τις κορυφές
είναι τα ίχνη των υψών από τις κορυφές  και
και  , αντίστοιχα. Η ευθεία που εφάπτεται στον περιγεγραμμένο κύκλο του τριγώνου
, αντίστοιχα. Η ευθεία που εφάπτεται στον περιγεγραμμένο κύκλο του τριγώνου  στο
στο  τέμνει την
τέμνει την  στο
στο  . Η ευθεία που είναι παράλληλη στην
. Η ευθεία που είναι παράλληλη στην  και διέρχεται από το
και διέρχεται από το  τέμνει την
τέμνει την  στο
στο  . Να αποδείξετε ότι η
. Να αποδείξετε ότι η  είναι κάθετη στη διάμεσο από το
είναι κάθετη στη διάμεσο από το  του τριγώνου
του τριγώνου  .
. έτσι ώστε να υπάρχουν
έτσι ώστε να υπάρχουν  αριθμοί μεταξύ δύο
αριθμοί μεταξύ δύο  , όταν
, όταν


 ,
,  είναι μια τέτοια διάταξη.)
είναι μια τέτοια διάταξη.)

 και η f 1-1.
και η f 1-1. και λαμβάνω ότι
και λαμβάνω ότι  τέτοιο ώστε
τέτοιο ώστε  (δεν το ρισκάρω με το επί του
(δεν το ρισκάρω με το επί του  )
) λαμβάνω
λαμβάνω 
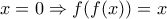

 :
: 

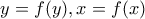 και:
και:  που είναι η (1).
που είναι η (1). καταλήγω στην:
καταλήγω στην:
 και έχω
και έχω  δηλαδή
δηλαδή  σταθερή.
σταθερή.
 (edit: διορθώθηκε μετά από ΠΜ του κ. Θανάση)
(edit: διορθώθηκε μετά από ΠΜ του κ. Θανάση)
 στην αρχική έχω:
στην αρχική έχω: 

 :
:  για
για  ,
,  και από την
και από την 
 δηλαδή f γνησίως αύξουσα και καταλήγω με
δηλαδή f γνησίως αύξουσα και καταλήγω με 

 .
. και
και 

 και αφού
και αφού 
![[m,n]=\frac{mn}{(m,n)}=\frac{mn}{d_1} [m,n]=\frac{mn}{(m,n)}=\frac{mn}{d_1}](/forum/ext/geomar/texintegr/latexrender/pictures/29c9af1f24e76117b39f9b4073f628c4.png)
![[m+1,n+1]=\frac{(m+1)(n+1)}
{(m+1,n+1)}=\frac{mn+m+n+1}{d_2}>\frac{mn}{d_2} [m+1,n+1]=\frac{(m+1)(n+1)}
{(m+1,n+1)}=\frac{mn+m+n+1}{d_2}>\frac{mn}{d_2}](/forum/ext/geomar/texintegr/latexrender/pictures/907794b8b2c49b966f0d10f904300521.png)
![[m,n]+[m+1,n+1]>mn(\frac{1}{d_1}+\frac{1}{d_2})\geq mn\cdot2\frac{1}{\sqrt{d_1d_2}}\geq\frac{2mn}{\sqrt{m-n}} [m,n]+[m+1,n+1]>mn(\frac{1}{d_1}+\frac{1}{d_2})\geq mn\cdot2\frac{1}{\sqrt{d_1d_2}}\geq\frac{2mn}{\sqrt{m-n}}](/forum/ext/geomar/texintegr/latexrender/pictures/6e99caa3dbc36eaf8dc6f759114cf442.png)
 σταθερό αλλάζοντας το
σταθερό αλλάζοντας το  εύκολα η
εύκολα η  είναι
είναι 
 παίρνω
παίρνω  δηλαδή
δηλαδή  .
. παίρνω
παίρνω  .
. δίνει
δίνει  .Η αρχική για
.Η αρχική για 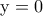 δίνει
δίνει  .
.
 και η απόδειξη ολοκληρώθηκε.
και η απόδειξη ολοκληρώθηκε. η τομή των
η τομή των  εγγράψιμο με κέντρο κύκλου το μέσο
εγγράψιμο με κέντρο κύκλου το μέσο  της
της  πολική του
πολική του  μεταξύ τους κάθετες.
μεταξύ τους κάθετες.
 η δέσμη
η δέσμη  είναι αρμονική. Έτσι, αν η
είναι αρμονική. Έτσι, αν η  στο
στο  ,
,  .
. παραλληλόγραμμο.
παραλληλόγραμμο. .
. παραλληλόγραμμο και το ζητούμενο έπεται.
παραλληλόγραμμο και το ζητούμενο έπεται.![\left [ m,n \right ]\leqslant mn, \left [ m+1,n+1 \right ]\leqslant (m+1)(n+1) \left [ m,n \right ]\leqslant mn, \left [ m+1,n+1 \right ]\leqslant (m+1)(n+1)](/forum/ext/geomar/texintegr/latexrender/pictures/7a198417c5db4c431c48ed044cfc8097.png) . Πρέπει, συνεπώς, να ισχύει ισοδύναμα:
. Πρέπει, συνεπώς, να ισχύει ισοδύναμα:  .
.![\displaystyle [m,n] + [m+1,n+1] \leqslant mn + (m+1)(n+1) \geqslant \frac{2mn}{\sqrt{m-n}} \displaystyle [m,n] + [m+1,n+1] \leqslant mn + (m+1)(n+1) \geqslant \frac{2mn}{\sqrt{m-n}}](/forum/ext/geomar/texintegr/latexrender/pictures/03ff5e3a517c9c26c2002f7e82e594cb.png)