Να βρείτε όλες τις πραγματικές λύσεις της εξίσωσης

ΘΕΜΑ 2
Σε ένα παραλληλόγραμμο
 είναι
είναι  .Έστω
.Έστω  η προβολή του
η προβολή του  στην
στην  και
και  το συμμετρικό του
το συμμετρικό του  ως προς την
ως προς την 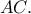 Να αποδειχθεί ότι
Να αποδειχθεί ότι  .
.ΘΕΜΑ 3
Να βρείτε όλους τους θετικούς ακέραιους
 με διαιρέτες τους αριθμούς
με διαιρέτες τους αριθμούς 
για τους οποίους ισχύει

ΘΕΜΑ 4
Έστω
 ένας δεκαεξαψήφιος θετικός ακέραιος αριθμός.
ένας δεκαεξαψήφιος θετικός ακέραιος αριθμός. Να αποδείξετε ότι υπάρχουν ένα ή περισσότερα διαδοχικά ψηφία του
 , το γινόμενο των οποίων είναι τέλειο τετράγωνο!
, το γινόμενο των οποίων είναι τέλειο τετράγωνο!

 και η
και η  με
με  άρτιο.
άρτιο.
 (επίσης γι αυτές τις τιμές δεν μηδενίζεται η βάση)
(επίσης γι αυτές τις τιμές δεν μηδενίζεται η βάση) (επίσης για τις τιμές αυτές
(επίσης για τις τιμές αυτές  .
. Αυτό συμβαίνει αν και μόνο αν:
Αυτό συμβαίνει αν και μόνο αν: και
και 
 και
και 
 και
και  άρτιος.
άρτιος.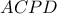 είναι ορθογώνιο εγγεγραμμένο σε κύκλο
είναι ορθογώνιο εγγεγραμμένο σε κύκλο  κι επειδή
κι επειδή  το
το  άρα
άρα 
 .
. περιττός.Τότε πρέπει
περιττός.Τότε πρέπει  περιττός άρα
περιττός άρα  άτοπο!
άτοπο! ,τότε
,τότε  άρα
άρα  άτοπο!
άτοπο! τότε
τότε 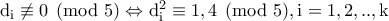 . Παίρνοντας τις περιπτώσεις
. Παίρνοντας τις περιπτώσεις  καταλήγουμε σε άτοπο.
καταλήγουμε σε άτοπο. .
. να είναι τετράγωνο κάποιου
να είναι τετράγωνο κάποιου  και αυτό γιατί
και αυτό γιατί 

 και
και 

 .Όμως η
.Όμως η  έχει θετική λύση για
έχει θετική λύση για  (ο τρόπος επίλυσης είναι απλός με διαφορά τετραγώνων κλπ).Αυτό όμως δεν μπορεί να συμβαίνει καθώς και οι
(ο τρόπος επίλυσης είναι απλός με διαφορά τετραγώνων κλπ).Αυτό όμως δεν μπορεί να συμβαίνει καθώς και οι  είναι διαιρέτες του
είναι διαιρέτες του  δεν είναι αρκετές.
δεν είναι αρκετές.

 τότε
τότε  που με παραγοντοποίηση κλπ δίνει
που με παραγοντοποίηση κλπ δίνει  .Η τιμή
.Η τιμή  απορρίπτεται αφού δεν θα υπήρχαν
απορρίπτεται αφού δεν θα υπήρχαν  για να αντιστοιχίσουμε όλους του διαιρέτες του
για να αντιστοιχίσουμε όλους του διαιρέτες του  .Για
.Για  θα είναι
θα είναι  και θα ισχύει η σχέση
και θα ισχύει η σχέση  .Αν
.Αν  τότε
τότε  άρα λόγω της
άρα λόγω της  θα είναι
θα είναι  δηλαδή
δηλαδή  .Αν θεωρήσω
.Αν θεωρήσω  τότε
τότε  αυτό όμως είναι άτοπο γιατί το
αυτό όμως είναι άτοπο γιατί το  έχει ''λίγους'' πρώτους διαιρέτες και έχουμε ήδη αρκετούς πρώτους διαιρέτες του
έχει ''λίγους'' πρώτους διαιρέτες και έχουμε ήδη αρκετούς πρώτους διαιρέτες του  δεν διαιρεί το
δεν διαιρεί το  τότε δεν μπορεί
τότε δεν μπορεί  αλλά βρίσκουμε ότι πρέπει
αλλά βρίσκουμε ότι πρέπει  άτοπο!
άτοπο! .Η
.Η  δίνει
δίνει  (αφού
(αφού  ) και
) και  .Επειδή σίγουρα τα
.Επειδή σίγουρα τα 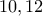 διαιρούν το \rm n θα είναι
διαιρούν το \rm n θα είναι 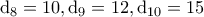 .Αν
.Αν  τότε από την
τότε από την  .Επειδή το
.Επειδή το  έχει ''λίγους'' διαιρέτες όπως πριν παίρνουμε άτοπο.Άρα
έχει ''λίγους'' διαιρέτες όπως πριν παίρνουμε άτοπο.Άρα 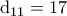 που δίνει
που δίνει  .Θεωρώντας την κανονική μορφή του
.Θεωρώντας την κανονική μορφή του  έπεται πως
έπεται πως  που όπως θα δούμε και παρακάτω αποτελεί την μοναδική λύση του προβλήματος.
που όπως θα δούμε και παρακάτω αποτελεί την μοναδική λύση του προβλήματος. .
. .
.
 .Τότε
.Τότε  .
. παίρνουμε ότι οι λύσεις είναι
παίρνουμε ότι οι λύσεις είναι  άτοπο.
άτοπο. είναι
είναι  .
.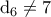 .Τότε ακριβώς όπως πριν
.Τότε ακριβώς όπως πριν 
 .
.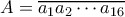 ο αριθμός. Κοιτάζουμε τους αριθμούς
ο αριθμός. Κοιτάζουμε τους αριθμούς  . Μπορούμε να γράψουμε
. Μπορούμε να γράψουμε  ως γινόμενο πρώτων παραγόντων. Κοιτάζουμε τα
ως γινόμενο πρώτων παραγόντων. Κοιτάζουμε τα  διανύσματα
διανύσματα  . Αν για κάποιο
. Αν για κάποιο  έχουμε
έχουμε  τότε το
τότε το  είναι τέλειο τετράγωνο και τελειώσαμε. Αλλιώς, από την αρχή του περιστερώνα θα έχουμε
είναι τέλειο τετράγωνο και τελειώσαμε. Αλλιώς, από την αρχή του περιστερώνα θα έχουμε  με
με  . Τότε το
. Τότε το  είναι τέλειο τετράγωνο και πάλι τελειώσαμε.
είναι τέλειο τετράγωνο και πάλι τελειώσαμε.