Υποθέτουμε ότι οι πραγματικοί αριθμοί
 δεν είναι ακέραιοι και το άθροισμα οποιονδήποτε τριών από αυτούς είναι ακέραιος.
δεν είναι ακέραιοι και το άθροισμα οποιονδήποτε τριών από αυτούς είναι ακέραιος. Είναι δυνατόν ο αριθμός
 να είναι ακέραιος;
να είναι ακέραιος; ΘΕΜΑ 2
Χρωματίζουμε κάθε σημείο του επιπέδου με ένα από
 χρώματα έτσι ώστε τα σημεία κάθε ευθείας του επιπέδου να είναι χρωματισμένα με το πολύ δύο χρώματα.
χρώματα έτσι ώστε τα σημεία κάθε ευθείας του επιπέδου να είναι χρωματισμένα με το πολύ δύο χρώματα. Να προσδιορίσετε τη μέγιστη τιμή του

ΘΕΜΑ 3
Θεωρούμε τρίγωνο
 με
με  και
και  To σημείο
To σημείο  βρίσκεται στην προέκταση της πλευράς
βρίσκεται στην προέκταση της πλευράς  προς το
προς το 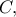 έτσι ώστε
έτσι ώστε  Να προσδιορίσετε το μέτρο της γωνίας
Να προσδιορίσετε το μέτρο της γωνίας 
ΘΕΜΑ 4
Να αποδείξετε ότι

για όλους τους θετικούς πραγματικούς αριθμούς
 και
και 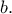

 όταν θέλω να συμβολίσω ακέραιο.
όταν θέλω να συμβολίσω ακέραιο.  οπότε με αφαίρεση
οπότε με αφαίρεση  . Όμοια
. Όμοια  , οπότε έχουμε
, οπότε έχουμε  . Λύνοντας ως προς
. Λύνοντας ως προς  για κάποιον ακέραιο
για κάποιον ακέραιο  . Έτσι
. Έτσι 
 και άρα
και άρα  διαιρεί τον
διαιρεί τον  . Συνεπώς o
. Συνεπώς o  είναι πολλαπλάσιο του
είναι πολλαπλάσιο του  ακέραιος. Άτοπο.
ακέραιος. Άτοπο. . Αν όλες οι ευθείες είναι μονοχρωματικές τότε έχουμε άτοπο αφού κάθε
. Αν όλες οι ευθείες είναι μονοχρωματικές τότε έχουμε άτοπο αφού κάθε  τεμνόμενες θα πρέπει να έχουν ένα κοινό χρώμα.Έστω λοιπόν δύο σημεία
τεμνόμενες θα πρέπει να έχουν ένα κοινό χρώμα.Έστω λοιπόν δύο σημεία  μιας ευθείες με χρώματα
μιας ευθείες με χρώματα  αντίστοιχα. Αφού
αντίστοιχα. Αφού  στο επίπεδο με χρώμα
στο επίπεδο με χρώμα  και τουλάχιστον ένα ακόμη
και τουλάχιστον ένα ακόμη  με χρώμα
με χρώμα 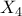 .Τότε όμως οι ευθείες
.Τότε όμως οι ευθείες  δεν έχουν κοινό χρώμα άρα θα πρέπει να είναι παράλληλες.Είναι σίγουρο όμως πως πάνω στην
δεν έχουν κοινό χρώμα άρα θα πρέπει να είναι παράλληλες.Είναι σίγουρο όμως πως πάνω στην  υπάρχει σημείο
υπάρχει σημείο  με χρώμα είτε
με χρώμα είτε  είτε
είτε  .Αν είναι
.Αν είναι  δεν είναι παράλληλες και έτσι καταλήξαμε σε άτοπο.Όμοια αν είναι
δεν είναι παράλληλες και έτσι καταλήξαμε σε άτοπο.Όμοια αν είναι  τέμνονται.
τέμνονται. .Η τιμή
.Η τιμή  είναι εφικτή όταν κάθε ευθεία έχει
είναι εφικτή όταν κάθε ευθεία έχει  είναι
είναι  και έχουμε να αποδείξουμε ότι
και έχουμε να αποδείξουμε ότι

 (παραβολή) που είναι γνησίως αύξουσα στο διάστημα
(παραβολή) που είναι γνησίως αύξουσα στο διάστημα 



 στην
στην  τέμνει την
τέμνει την  στο
στο  .Είναι
.Είναι 
 και αφού
και αφού  από
από 
 είναι ορθογώνιο με
είναι ορθογώνιο με  άρα
άρα 
 με πρόσθεση δίνουν
με πρόσθεση δίνουν  . Επιπλέον
. Επιπλέον 



 στο
στο 
 ώστε
ώστε  .
. 
 τέμνει την
τέμνει την  στο
στο  .
. .
.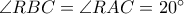 , οπότε
, οπότε  , και αφού
, και αφού  , προκύπτει
, προκύπτει  , οπότε
, οπότε  .
. .
. , συνεπώς
, συνεπώς  .
.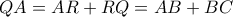 .
. 
 , από τον Ισχυρισμό.
, από τον Ισχυρισμό. είναι ισοσκελές, με
είναι ισοσκελές, με  , συνεπώς
, συνεπώς  .
. και
και 



 .
.