socrates έγραψε: ↑Δευ Μαρ 09, 2020 2:04 am
ΘΕΜΑ 3
Να βρείτε τον μικρότερο θετικό ακέραιο

με την ιδιότητα:
Αν βάψουμε μαύρα ακριβώς

κελιά ενός πίνακα

τότε υπάρχει οπωσδήποτε ένα

τετράγωνο με τουλάχιστον τρία μαύρα κελιά.
Αλλιώς:
Έστω, προς άτοπο, ότι δεν υπάρχει

τετράγωνο με τουλάχιστον τρία μαύρα κελιά.
Παίρνουμε το πάνω αριστερά
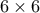
τετράγωνο, το οποίο χωρίζουμε σε 9 τετράγωνα
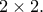
Καθένα από τα

τετράγωνα έχει το πολύ δύο μαύρα κελιά, άρα στο

υπάρχουν το πολύ 18 μαύρα κελιά.
Τα υπόλοιπα 11 τουλάχιστον μαύρα βρίσκονται στην 7η γραμμή ή στην 7η στήλη. Η 7η γραμμή και η 7η στήλη έχουν μαζί 13 κελιά.
Άρα το πολύ δύο θα είναι λευκά.
Αν όλα τα κελιά είναι μαύρα, τότε έχουμε άτοπο από το

τετράγωνο κάτω δεξιά.
Αν 12 κελιά είναι μαύρα,
- αν το κελί κάτω δεξιά είναι μαύρο, το κελί (6,7) ή το (7,6) είναι μαύρο και το άλλο άσπρο. Έστω το (7,6). Η τελευταία γραμμή είναι τότε όλη μαύρη οπότε η 6η γραμμή και η 6η στήλη όλη άσπρη. Άρα στο πάνω αριστερά
 τετράγωνο υπάρχουν 17 μαύρα κελιά.
τετράγωνο υπάρχουν 17 μαύρα κελιά.
Παρόμοια, το χωρίζουμε σε ένα  τετράγωνο και ένα "γάμμα". Στο
τετράγωνο και ένα "γάμμα". Στο  τετράγωνο υπάρχουν 4 τετράγωνα
τετράγωνο υπάρχουν 4 τετράγωνα  , στα οποία υπάρχουν συνολικά το πολύ 8 μαύρα κελιά, οπότε στο γάμμα υπάρχουν 9, άτοπο.
, στα οποία υπάρχουν συνολικά το πολύ 8 μαύρα κελιά, οπότε στο γάμμα υπάρχουν 9, άτοπο.
- αν το κελί κάτω δεξιά είναι άσπρο τότε τα (6,7) και (7,6) είναι μαύρα. Δουλεύοντας παρόμοια με πριν, η 6η γραμμή και η 6η στήλη είναι όλη άσπρη. Άρα στο πάνω αριστερά
 τετράγωνο υπάρχουν 17 μαύρα κελιά κτλ...
τετράγωνο υπάρχουν 17 μαύρα κελιά κτλ...
Αν 11 κελιά είναι μαύρα, τότε σε κάθε τετράγωνο

του πάνω αριστερά
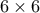
υπάρχουν ακριβώς 2 μαύρα.
- αν το κελί κάτω δεξιά είναι μαύρο, τότε
-- αν τα (6,7) και (7,6) είναι άσπρα τότε βάφοντας κατάλληλα τη σκακιέρα από κάτω προς τα πάνω έχουμε άτοπο στην 3η γραμμή
-- αν π.χ. το (6,7) είναι μαύρο και το (7,6) άσπρο, βάφοντας κατάλληλα τη σκακιέρα από κάτω προς τα πάνω έχουμε άτοπο.
- αν το κελί κάτω δεξιά είναι άσπρο, τότε τότε η υπόλοιπη 7η γραμμή ή στήλη θα είναι μαύρη. Βάφοντας κατάλληλα τη σκακιέρα από κάτω προς τα πάνω έχουμε άτοπο.
Ελπίζω να είναι κατανοητό!

 ,
,  ,
,  είναι διαφορετικοί από το
είναι διαφορετικοί από το  και ισχύει:
και ισχύει: 


 , για τα οποία ο αριθμός
, για τα οποία ο αριθμός  είναι πολλαπλάσιο του
είναι πολλαπλάσιο του  .
. με την ιδιότητα:
με την ιδιότητα:  κελιά ενός πίνακα
κελιά ενός πίνακα  τότε υπάρχει οπωσδήποτε ένα
τότε υπάρχει οπωσδήποτε ένα  τετράγωνο με τουλάχιστον τρία μαύρα κελιά.
τετράγωνο με τουλάχιστον τρία μαύρα κελιά.  , η εξωτερική διχοτόμος της γωνίας
, η εξωτερική διχοτόμος της γωνίας  τέμνει την ευθεία
τέμνει την ευθεία  στο
στο  . Τα ίχνη των καθέτων από τα σημεία
. Τα ίχνη των καθέτων από τα σημεία  και
και  στην ευθεία
στην ευθεία  είναι τα
είναι τα  και
και  , αντίστοιχα, ενώ το ίχνος της κάθετης από το
, αντίστοιχα, ενώ το ίχνος της κάθετης από το  στην
στην  είναι το
είναι το  .
.  .
.

 (3) οπότε
(3) οπότε 






 άτοπο
άτοπο (4)
(4)

 .Επίσης
.Επίσης  .Από τα παραπάνω έπεται ότι
.Από τα παραπάνω έπεται ότι  .
. τότε πρέπει
τότε πρέπει  το οποίο είναι προφανώς αδύνατον.
το οποίο είναι προφανώς αδύνατον. τότε
τότε 
 είναι
είναι  άρα
άρα  .
.

 ,όμως
,όμως  άρα
άρα  που δίνει τις λύσεις
που δίνει τις λύσεις 

 .'Ομως
.'Ομως  άρα
άρα  από όπου
από όπου 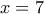 .
.
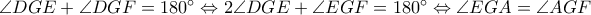 .
. να είναι διχοτόμος της
να είναι διχοτόμος της  .
. από όπου έπεται το ζητούμενο αφού
από όπου έπεται το ζητούμενο αφού 
 πρέπει να το μελετήσουμε ξεχωριστά, καθώς τότε δεν ισχύει απαραίτητα
πρέπει να το μελετήσουμε ξεχωριστά, καθώς τότε δεν ισχύει απαραίτητα 
 τότε
τότε  ή
ή  !
! άρα πρέπει
άρα πρέπει 
 με
με  φυσικό.
φυσικό. .
. .Θα αποδείξω πως για
.Θα αποδείξω πως για  υπάρχει πάντα ένα
υπάρχει πάντα ένα  διαδοχικές στήλες (με όλες τις γραμμές) προκύπτει εάν ο χρωματισμός είναι τέτοιος ώστε σε κάθε
διαδοχικές στήλες (με όλες τις γραμμές) προκύπτει εάν ο χρωματισμός είναι τέτοιος ώστε σε κάθε  μαύρα κελιά.
μαύρα κελιά.
 μαζί έχουν το πολύ
μαζί έχουν το πολύ  .Έτσι λοιπόν οι σι στήλες
.Έτσι λοιπόν οι σι στήλες  μαζί έχουν τουλάχιστον
μαζί έχουν τουλάχιστον  μαύρα κελιά.
μαύρα κελιά. στήλες υπάρχουν
στήλες υπάρχουν  .Έχουμε
.Έχουμε 
 μαύρα κελιά τότε προκειμένου να μην ισχύει το ζητούμενο η
μαύρα κελιά τότε προκειμένου να μην ισχύει το ζητούμενο η  τότε
τότε  άρα θα πρέπει οι
άρα θα πρέπει οι  στήλες να έχουν συνολικά περισσότερα ή ίσα από
στήλες να έχουν συνολικά περισσότερα ή ίσα από  μαύρα.Επειδή όμως το
μαύρα.Επειδή όμως το  το οποίο οδηγεί εύκολα σε άτοπο.
το οποίο οδηγεί εύκολα σε άτοπο. μαύρα τότε η
μαύρα τότε η  τότε
τότε  άρα οι
άρα οι 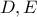 έχουν περισσότερα ή ίσα από
έχουν περισσότερα ή ίσα από  μαύρα.Επειδή όμως το
μαύρα.Επειδή όμως το  άτοπο αφού η
άτοπο αφού η 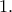
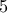 τότε οι
τότε οι 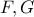 έχουν
έχουν 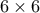 τετράγωνο, το οποίο χωρίζουμε σε 9 τετράγωνα
τετράγωνο, το οποίο χωρίζουμε σε 9 τετράγωνα 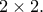
 τετράγωνα έχει το πολύ δύο μαύρα κελιά, άρα στο
τετράγωνα έχει το πολύ δύο μαύρα κελιά, άρα στο  υπάρχουν το πολύ 18 μαύρα κελιά.
υπάρχουν το πολύ 18 μαύρα κελιά.  τετράγωνο υπάρχουν 17 μαύρα κελιά.
τετράγωνο υπάρχουν 17 μαύρα κελιά.  τετράγωνο και ένα "γάμμα". Στο
τετράγωνο και ένα "γάμμα". Στο