Σελίδα 1 από 1
Τεστ Εξάσκησης!
Δημοσιεύτηκε: Σάβ Μαρ 07, 2020 1:42 pm
από Ορέστης Λιγνός
Ένα τεστ εξάσκησης για Μεγάλους.
Όλες οι ασκήσεις είναι δικής μου κατασκευής.
Enjoy them!
 Πρόβλημα 1
Πρόβλημα 1
Στον πίνακα είναι γραμμένοι οι αριθμοί

. Ο Δημήτρης κάνει την εξής κίνηση:

Επιλέγει δύο διαφορετικούς μεταξύ τους αριθμούς του πίνακα, που είναι ισοϋπόλοιποι

, τους σβήνει και τους αντικαθιστά γράφοντας δύο φορές τον μέσο όρο τους (έτσι αν επιλέξει τους

, τους σβήνει και γράφει

).
Ορίζουμε ως
αξία του πίνακα, το άθροισμα των τετράγωνων των αριθμών του πίνακα. Έτσι, η αξία του πίνακα στην αρχή είναι

. Να βρείτε τη μέγιστη τιμή της αξίας του πίνακα μετά από

κινήσεις.
Πρόβλημα 2
Να βρείτε την ελάχιστη τιμή του θετικού ακέραιου

, ώστε να ικανοποιούνται οι δύο παρακάτω συνθήκες:



υπάρχει θετικός ακέραιος

,
σχετικά πρώτος με τον 
, ώστε ο

να είναι τέλειο τετράγωνο.
Πρόβλημα 3
Έστω

οξυγώνιο τρίγωνο και

τα ύψη τους. Έστω

το σημείο τομής της
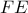
με τον περιγεγραμμένο κύκλο

του

με το

να ανήκει στο μικρό τόξο

. Αν τέλος

το σημείο τομής της

με τον

, να δείξετε την πιο κάτω ισοδυναμία:

αρμονικό τετράπλευρο.
Πρόβλημα 4
Να βρείτε όλες τις συναρτήσεις

, ώστε:

, για κάθε

.
Edit: Προσθήκη στο Πρόβλημα 2 ... (η αρχική μορφή της εκφώνησης καθιστούσε το πρόβλημα προφανές καθώς αρκούσε να επιλέξουμε  ...
...
Re: Τεστ Εξάσκησης!
Δημοσιεύτηκε: Σάβ Μαρ 07, 2020 6:49 pm
από min##
Καλησπέρα Ορέστη.
4.Συμβολίζω με

τη σχέση.
Αρχικά είναι απλό πως η

είναι

και επί.
Έχω:


από όπου

(αφού η

είναι

).
Το

τώρα, δίνει πως

περιττή.
Έτσι,το

δίνει

.
Για

μπορώ να έχω

για οποιοδήποτε

με κατάλληλο

(

επί..).Ακόμα,για

το

παίρνει την τιμή

που απομένει.
Μ'αυτά και μ'αυτά,η παραπάνω ανάγεται στην

.
Συνεπώς,η

γίνεται

.
Από το

προκύπτει τελικά πως η

είναι γραμμική.
Αντικαθιστώντας στην αρχική,μόνο η

επαληθεύει κλπ.
υγ...Και κατασκευαστής ο δικός σου


Μπράβο..
Re: Τεστ Εξάσκησης!
Δημοσιεύτηκε: Σάβ Μαρ 07, 2020 7:14 pm
από ΦΩΤΙΑΔΗΣ ΠΡΟΔΡΟΜΟΣ
Ορέστης Λιγνός έγραψε: ↑Σάβ Μαρ 07, 2020 1:42 pm
Πρόβλημα 1
Στον πίνακα είναι γραμμένοι οι αριθμοί

. Ο Δημήτρης κάνει την εξής κίνηση:

Επιλέγει δύο διαφορετικούς μεταξύ τους αριθμούς του πίνακα, που είναι ισοϋπόλοιποι

, τους σβήνει και τους αντικαθιστά γράφοντας δύο φορές τον μέσο όρο τους (έτσι αν επιλέξει τους

, τους σβήνει και γράφει

).
Ορίζουμε ως
αξία του πίνακα, το άθροισμα των τετράγωνων των αριθμών του πίνακα. Έτσι, η αξία του πίνακα στην αρχή είναι

. Να βρείτε τη μέγιστη τιμή της αξίας του πίνακα μετά από

κινήσεις.
Καλησπέρα Ορέστη!
Έστω ότι σε κάποιο βήμα έχουμε επιλέξει τους

με
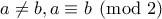
.Τότε αν

η προηγούμενη αξία του πίνακα τότε η νέα θα είναι

Άρα όσο μικραίνει το

τόσο θα μεγαλώνει η νέα αξία( η οποία όμως πάντα θα είναι μικρότερη του

).
Επειδή

είναι

.Έτσι σε κάθε βήμα η αξία του πίνακα μειώνεται κατά τουλάχιστον

.
Έτσι αν κάνουμε τις παρακάτω κινήσεις θα βρούμε την μέγιστη αξία μετά από

κινήσεις:

Ο τελευταίος πίνακας έχει αξία

.
Re: Τεστ Εξάσκησης!
Δημοσιεύτηκε: Δευ Μαρ 09, 2020 2:19 pm
από stamas1
Για το 2 προβλημα λυση??
Re: Τεστ Εξάσκησης!
Δημοσιεύτηκε: Τετ Μαρ 11, 2020 10:01 pm
από Ορέστης Λιγνός
Επαναφορά για τα προβλήματα 2 και 3 !!

Re: Τεστ Εξάσκησης!
Δημοσιεύτηκε: Πέμ Μαρ 12, 2020 12:23 am
από min##
Γεωμε3:
Εξετάζουμε τις 2 υποθέσεις ξεχωριστά για αρχή :
H ισότητα

ισοδυναμεί με την εγγραψιμότητα του

.
Πράγματι,

διότι

.
Η υπόθεση

αρμονικό ισοδυναμεί με την ισότητα

(απλά προβάλλουμε το τετράπλευρο από το

στην

.)
Ισοδυναμεί λοιπόν με

ή από

με

εγγράψιμο,όπου
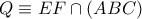
.
Θέμε να δείξουμε πως από τη μια εγγραψιμότητα έπεται η άλλη.
Αρκεί από Ριζικούς άξονες νδο. οι
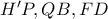
είναι συντρέχουσες.
Ας υποθέσουμε ότι έχουμε την εγγραψιμότητα του

.(η αντίστροφη πορεία προκύπτει εύκολα με βάση τα παρακάτω).
Ας είναι
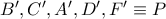
τα συμμετρικά των
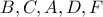
ως προς το

αντίστοιχα.
Από υπόθεση (

εγγράψιμο/

παράλληλες) βλέπουμε πως

.
Λόγω συμμετρίας,το
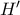
είναι το Ορθόκεντρο του
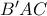
και το

είναι εγγράψιμο.
Είναι γνωστό ότι η τομή των
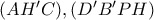
-το

δηλαδή-ανήκει στη διάμεσο του
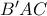
ως προς

.
Αφού λοιπόν λόγω συμμετρίας τα

είναι συνευθειακά,προκύπτει ότι το

είναι το μέσον της

.
Πάλι λόγω συμμετρίας τα

είναι συνευθειακά,οπότε πάλι από γνωστή πρόταση

.
Από ριζικούς άξονες (

) ή συμμετρία έπεται ότι

συνευθειακά,οπότε ως γνωστόν
το

είναι το αρμονικό συζυγές του

ως προς τα

.
Έτσι,

και

συνευθειακά,δηλαδή οι
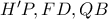
συντρέχουν στο

που είναι το ζητούμενο..

- orestis3.png (24.57 KiB) Προβλήθηκε 2343 φορές
Re: Τεστ Εξάσκησης!
Δημοσιεύτηκε: Τρί Ιουν 23, 2020 10:09 pm
από ΦΩΤΙΑΔΗΣ ΠΡΟΔΡΟΜΟΣ
Ορέστης Λιγνός έγραψε: ↑Σάβ Μαρ 07, 2020 1:42 pm
Πρόβλημα 2
Να βρείτε την ελάχιστη τιμή του θετικού ακέραιου

, ώστε να ικανοποιούνται οι δύο παρακάτω συνθήκες:



υπάρχει θετικός ακέραιος

,
σχετικά πρώτος με τον 
, ώστε ο

να είναι τέλειο τετράγωνο.
Με επιφυλάξεις...
Έστω

.Οπότε έχουμε 2 περιπτώσεις:
 με
με 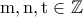
Με αντικατάσταση του  παίρνουμε
παίρνουμε  και επειδή
και επειδή  θα είναι
θα είναι  .Άρα θέλουμε
.Άρα θέλουμε  .Επειδή
.Επειδή  πρέπει
πρέπει  .
.
Θεωρώ το παραπάνω ως τριώνυμο του  οπότε η διακρίνουσα
οπότε η διακρίνουσα  πρέπει να είναι τέλειο τετράγωνο ,έστω
πρέπει να είναι τέλειο τετράγωνο ,έστω 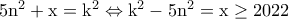
.Είναι  ,από όπου εύκολα
,από όπου εύκολα  .
.
Είναι  .Άρα ελέγχουμε την περίπτωση
.Άρα ελέγχουμε την περίπτωση 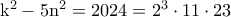 .Θα είναι
.Θα είναι  .Θα πρέπει
.Θα πρέπει 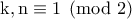 τότε
τότε  άτοπο.
άτοπο.
Έστω 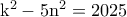 .Προφανώς
.Προφανώς 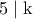 ,έστω
,έστω  .Γίνεται
.Γίνεται  .Από εδώ
.Από εδώ  άτοπο.
άτοπο.
Αν  τότε αναγκαστικά
τότε αναγκαστικά  άτοπο.
άτοπο.
Πάμε στην  .Αυτή για
.Αυτή για 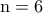 δίνει
δίνει  ,δεκτή λύση αφού
,δεκτή λύση αφού  .Αντικαθιστώντας βρίσκουμε
.Αντικαθιστώντας βρίσκουμε  που είναι σχετικά πρώτος με το
που είναι σχετικά πρώτος με το  και η δοθείσα παράσταση είναι τέλειο τετράγωνο.
και η δοθείσα παράσταση είναι τέλειο τετράγωνο.
 .Όπως πριν
.Όπως πριν  και έτσι
και έτσι  .Πάλι θεωρούμε ως τριώνυμο του
.Πάλι θεωρούμε ως τριώνυμο του  με διακρίνουσα
με διακρίνουσα  .Πρέπει να είναι τέλειο τετράγωνο,έστω
.Πρέπει να είναι τέλειο τετράγωνο,έστω  .Άν υπάρχει μικρότερη τιμή για το
.Άν υπάρχει μικρότερη τιμή για το  απ΄αυτή της πρώτης περίπτωσης θα είναι
απ΄αυτή της πρώτης περίπτωσης θα είναι  .Οπότε έχουμε
.Οπότε έχουμε  .
.
Αν  είναι
είναι  άτοπο.
άτοπο.
Επίσης  , έτσι όλες οι παραπάνω απορρίπτονται.
, έτσι όλες οι παραπάνω απορρίπτονται.
Η ζητούμενη τιμή λοιπόν είναι

Re: Τεστ Εξάσκησης!
Δημοσιεύτηκε: Παρ Ιουν 26, 2020 5:33 pm
από Ορέστης Λιγνός
ΦΩΤΙΑΔΗΣ ΠΡΟΔΡΟΜΟΣ έγραψε: ↑Τρί Ιουν 23, 2020 10:09 pm
Ορέστης Λιγνός έγραψε: ↑Σάβ Μαρ 07, 2020 1:42 pm
Πρόβλημα 2
Να βρείτε την ελάχιστη τιμή του θετικού ακέραιου

, ώστε να ικανοποιούνται οι δύο παρακάτω συνθήκες:



υπάρχει θετικός ακέραιος

,
σχετικά πρώτος με τον 
, ώστε ο

να είναι τέλειο τετράγωνο.
Με επιφυλάξεις...
Έστω

.Οπότε έχουμε 2 περιπτώσεις:
 με
με 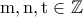
Με αντικατάσταση του  παίρνουμε
παίρνουμε  και επειδή
και επειδή  θα είναι
θα είναι  .Άρα θέλουμε
.Άρα θέλουμε  .Επειδή
.Επειδή  πρέπει
πρέπει  .
.
Θεωρώ το παραπάνω ως τριώνυμο του  οπότε η διακρίνουσα
οπότε η διακρίνουσα  πρέπει να είναι τέλειο τετράγωνο ,έστω
πρέπει να είναι τέλειο τετράγωνο ,έστω 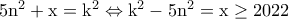
.Είναι  ,από όπου εύκολα
,από όπου εύκολα  .
.
Είναι  .Άρα ελέγχουμε την περίπτωση
.Άρα ελέγχουμε την περίπτωση 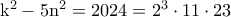 .Θα είναι
.Θα είναι  .Θα πρέπει
.Θα πρέπει 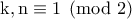 τότε
τότε  άτοπο.
άτοπο.
Έστω 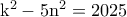 .Προφανώς
.Προφανώς 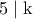 ,έστω
,έστω  .Γίνεται
.Γίνεται  .Από εδώ
.Από εδώ  άτοπο.
άτοπο.
Αν  τότε αναγκαστικά
τότε αναγκαστικά  άτοπο.
άτοπο.
Πάμε στην  .Αυτή για
.Αυτή για 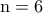 δίνει
δίνει  ,δεκτή λύση αφού
,δεκτή λύση αφού  .Αντικαθιστώντας βρίσκουμε
.Αντικαθιστώντας βρίσκουμε  που είναι σχετικά πρώτος με το
που είναι σχετικά πρώτος με το  και η δοθείσα παράσταση είναι τέλειο τετράγωνο.
και η δοθείσα παράσταση είναι τέλειο τετράγωνο.
 .Όπως πριν
.Όπως πριν  και έτσι
και έτσι  .Πάλι θεωρούμε ως τριώνυμο του
.Πάλι θεωρούμε ως τριώνυμο του  με διακρίνουσα
με διακρίνουσα  .Πρέπει να είναι τέλειο τετράγωνο,έστω
.Πρέπει να είναι τέλειο τετράγωνο,έστω  .Άν υπάρχει μικρότερη τιμή για το
.Άν υπάρχει μικρότερη τιμή για το  απ΄αυτή της πρώτης περίπτωσης θα είναι
απ΄αυτή της πρώτης περίπτωσης θα είναι  .Οπότε έχουμε
.Οπότε έχουμε  .
.
Αν  είναι
είναι  άτοπο.
άτοπο.
Επίσης  , έτσι όλες οι παραπάνω απορρίπτονται.
, έτσι όλες οι παραπάνω απορρίπτονται.
Η ζητούμενη τιμή λοιπόν είναι

Πολύ ωραία λύση Πρόδρομε!

Re: Τεστ Εξάσκησης!
Δημοσιεύτηκε: Τρί Ιουν 30, 2020 8:07 pm
από stamas1
Μπορεί κάποιος να γράψει την απόδειξη οτι η F(x) ειναι 1-1 και επι?
Re: Τεστ Εξάσκησης!
Δημοσιεύτηκε: Τρί Ιουν 30, 2020 11:05 pm
από giannisd
stamas1 έγραψε: ↑Τρί Ιουν 30, 2020 8:07 pm
Μπορεί κάποιος να γράψει την απόδειξη οτι η F(x) ειναι 1-1 και επι?
Επί:
Σταθεροποιώντας το

το
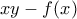
διατρέχει όλο το

για τις διάφορες τιμές του

.
1-1:
Βάλε

και θα το δεις μόνος σου.
Re: Τεστ Εξάσκησης!
Δημοσιεύτηκε: Σάβ Μάιος 01, 2021 12:04 pm
από 2nisic
Ορέστης Λιγνός έγραψε: ↑Σάβ Μαρ 07, 2020 1:42 pm
Να βρείτε την ελάχιστη τιμή του θετικού ακέραιου

, ώστε να ικανοποιούνται οι δύο παρακάτω συνθήκες:



υπάρχει θετικός ακέραιος

,
σχετικά πρώτος με τον 
, ώστε ο

να είναι τέλειο τετράγωνο.
Έστω
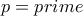
και

τότε θα πρέπει:

Άρα αν

τότε

η

.
Αν ο

τότε

δεινή

.
Αν ο
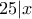
τότε

.
Άρα

αφού
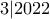
,

,

,

,

.
Για
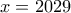
μπορούμε να πάρουμε
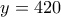
.

 . Ο Δημήτρης κάνει την εξής κίνηση:
. Ο Δημήτρης κάνει την εξής κίνηση: Επιλέγει δύο διαφορετικούς μεταξύ τους αριθμούς του πίνακα, που είναι ισοϋπόλοιποι
Επιλέγει δύο διαφορετικούς μεταξύ τους αριθμούς του πίνακα, που είναι ισοϋπόλοιποι  , τους σβήνει και τους αντικαθιστά γράφοντας δύο φορές τον μέσο όρο τους (έτσι αν επιλέξει τους
, τους σβήνει και τους αντικαθιστά γράφοντας δύο φορές τον μέσο όρο τους (έτσι αν επιλέξει τους  , τους σβήνει και γράφει
, τους σβήνει και γράφει  ).
). . Να βρείτε τη μέγιστη τιμή της αξίας του πίνακα μετά από
. Να βρείτε τη μέγιστη τιμή της αξίας του πίνακα μετά από  κινήσεις.
κινήσεις. , ώστε να ικανοποιούνται οι δύο παρακάτω συνθήκες:
, ώστε να ικανοποιούνται οι δύο παρακάτω συνθήκες:

 υπάρχει θετικός ακέραιος
υπάρχει θετικός ακέραιος  , σχετικά πρώτος με τον
, σχετικά πρώτος με τον  , ώστε ο
, ώστε ο  να είναι τέλειο τετράγωνο.
να είναι τέλειο τετράγωνο. οξυγώνιο τρίγωνο και
οξυγώνιο τρίγωνο και  τα ύψη τους. Έστω
τα ύψη τους. Έστω  το σημείο τομής της
το σημείο τομής της 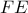 με τον περιγεγραμμένο κύκλο
με τον περιγεγραμμένο κύκλο  του
του  με το
με το  να ανήκει στο μικρό τόξο
να ανήκει στο μικρό τόξο  . Αν τέλος
. Αν τέλος  το σημείο τομής της
το σημείο τομής της  με τον
με τον  , να δείξετε την πιο κάτω ισοδυναμία:
, να δείξετε την πιο κάτω ισοδυναμία: αρμονικό τετράπλευρο.
αρμονικό τετράπλευρο. , ώστε:
, ώστε: , για κάθε
, για κάθε  .
. ...
... . Ο Δημήτρης κάνει την εξής κίνηση:
. Ο Δημήτρης κάνει την εξής κίνηση: Επιλέγει δύο διαφορετικούς μεταξύ τους αριθμούς του πίνακα, που είναι ισοϋπόλοιποι
Επιλέγει δύο διαφορετικούς μεταξύ τους αριθμούς του πίνακα, που είναι ισοϋπόλοιποι  , τους σβήνει και τους αντικαθιστά γράφοντας δύο φορές τον μέσο όρο τους (έτσι αν επιλέξει τους
, τους σβήνει και τους αντικαθιστά γράφοντας δύο φορές τον μέσο όρο τους (έτσι αν επιλέξει τους  , τους σβήνει και γράφει
, τους σβήνει και γράφει  ).
). . Να βρείτε τη μέγιστη τιμή της αξίας του πίνακα μετά από
. Να βρείτε τη μέγιστη τιμή της αξίας του πίνακα μετά από  κινήσεις.
κινήσεις. , ώστε να ικανοποιούνται οι δύο παρακάτω συνθήκες:
, ώστε να ικανοποιούνται οι δύο παρακάτω συνθήκες:

 υπάρχει θετικός ακέραιος
υπάρχει θετικός ακέραιος  , σχετικά πρώτος με τον
, σχετικά πρώτος με τον  , ώστε ο
, ώστε ο  να είναι τέλειο τετράγωνο.
να είναι τέλειο τετράγωνο. οξυγώνιο τρίγωνο και
οξυγώνιο τρίγωνο και  τα ύψη τους. Έστω
τα ύψη τους. Έστω  το σημείο τομής της
το σημείο τομής της 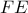 με τον περιγεγραμμένο κύκλο
με τον περιγεγραμμένο κύκλο  του
του  με το
με το  να ανήκει στο μικρό τόξο
να ανήκει στο μικρό τόξο  . Αν τέλος
. Αν τέλος  το σημείο τομής της
το σημείο τομής της  με τον
με τον  , να δείξετε την πιο κάτω ισοδυναμία:
, να δείξετε την πιο κάτω ισοδυναμία: αρμονικό τετράπλευρο.
αρμονικό τετράπλευρο. , ώστε:
, ώστε: , για κάθε
, για κάθε  .
. ...
... τη σχέση.
τη σχέση. είναι
είναι  και επί.
και επί.
 από όπου
από όπου  (αφού η
(αφού η  τώρα, δίνει πως
τώρα, δίνει πως  δίνει
δίνει  .
. μπορώ να έχω
μπορώ να έχω  για οποιοδήποτε
για οποιοδήποτε  με κατάλληλο
με κατάλληλο  το
το  παίρνει την τιμή
παίρνει την τιμή  που απομένει.
που απομένει. .
. .
. προκύπτει τελικά πως η
προκύπτει τελικά πως η  επαληθεύει κλπ.
επαληθεύει κλπ. με
με 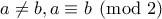 .Τότε αν
.Τότε αν  η προηγούμενη αξία του πίνακα τότε η νέα θα είναι
η προηγούμενη αξία του πίνακα τότε η νέα θα είναι 
 τόσο θα μεγαλώνει η νέα αξία( η οποία όμως πάντα θα είναι μικρότερη του
τόσο θα μεγαλώνει η νέα αξία( η οποία όμως πάντα θα είναι μικρότερη του  είναι
είναι  .Έτσι σε κάθε βήμα η αξία του πίνακα μειώνεται κατά τουλάχιστον
.Έτσι σε κάθε βήμα η αξία του πίνακα μειώνεται κατά τουλάχιστον  .
.
 .
. ισοδυναμεί με την εγγραψιμότητα του
ισοδυναμεί με την εγγραψιμότητα του  .
. διότι
διότι  .
. αρμονικό ισοδυναμεί με την ισότητα
αρμονικό ισοδυναμεί με την ισότητα  (απλά προβάλλουμε το τετράπλευρο από το
(απλά προβάλλουμε το τετράπλευρο από το  στην
στην  .)
.) ή από
ή από  με
με  εγγράψιμο,όπου
εγγράψιμο,όπου 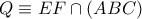 .
.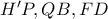 είναι συντρέχουσες.
είναι συντρέχουσες. .(η αντίστροφη πορεία προκύπτει εύκολα με βάση τα παρακάτω).
.(η αντίστροφη πορεία προκύπτει εύκολα με βάση τα παρακάτω).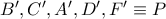 τα συμμετρικά των
τα συμμετρικά των 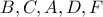 ως προς το
ως προς το  αντίστοιχα.
αντίστοιχα. εγγράψιμο/
εγγράψιμο/ παράλληλες) βλέπουμε πως
παράλληλες) βλέπουμε πως  .
.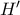 είναι το Ορθόκεντρο του
είναι το Ορθόκεντρο του 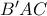 και το
και το  είναι εγγράψιμο.
είναι εγγράψιμο.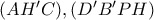 -το
-το  .
. είναι συνευθειακά,προκύπτει ότι το
είναι συνευθειακά,προκύπτει ότι το  είναι το μέσον της
είναι το μέσον της  .
. είναι συνευθειακά,οπότε πάλι από γνωστή πρόταση
είναι συνευθειακά,οπότε πάλι από γνωστή πρόταση  .
. ) ή συμμετρία έπεται ότι
) ή συμμετρία έπεται ότι  συνευθειακά,οπότε ως γνωστόν
συνευθειακά,οπότε ως γνωστόν είναι το αρμονικό συζυγές του
είναι το αρμονικό συζυγές του  .
. και
και  συνευθειακά,δηλαδή οι
συνευθειακά,δηλαδή οι 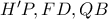 συντρέχουν στο
συντρέχουν στο  .Οπότε έχουμε 2 περιπτώσεις:
.Οπότε έχουμε 2 περιπτώσεις:
 με
με 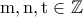
 παίρνουμε
παίρνουμε  και επειδή
και επειδή  θα είναι
θα είναι  .Άρα θέλουμε
.Άρα θέλουμε  .Επειδή
.Επειδή  πρέπει
πρέπει  .
. οπότε η διακρίνουσα
οπότε η διακρίνουσα  πρέπει να είναι τέλειο τετράγωνο ,έστω
πρέπει να είναι τέλειο τετράγωνο ,έστω 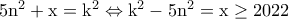
 ,από όπου εύκολα
,από όπου εύκολα  .
. .Άρα ελέγχουμε την περίπτωση
.Άρα ελέγχουμε την περίπτωση 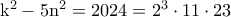 .Θα είναι
.Θα είναι  .Θα πρέπει
.Θα πρέπει 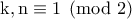 τότε
τότε  άτοπο.
άτοπο.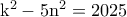 .Προφανώς
.Προφανώς 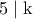 ,έστω
,έστω  .Γίνεται
.Γίνεται  .Από εδώ
.Από εδώ  άτοπο.
άτοπο. τότε αναγκαστικά
τότε αναγκαστικά  άτοπο.
άτοπο. .Αυτή για
.Αυτή για 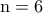 δίνει
δίνει  ,δεκτή λύση αφού
,δεκτή λύση αφού  .Αντικαθιστώντας βρίσκουμε
.Αντικαθιστώντας βρίσκουμε  που είναι σχετικά πρώτος με το
που είναι σχετικά πρώτος με το  και η δοθείσα παράσταση είναι τέλειο τετράγωνο.
και η δοθείσα παράσταση είναι τέλειο τετράγωνο. .Όπως πριν
.Όπως πριν  .Πάλι θεωρούμε ως τριώνυμο του
.Πάλι θεωρούμε ως τριώνυμο του  .Πρέπει να είναι τέλειο τετράγωνο,έστω
.Πρέπει να είναι τέλειο τετράγωνο,έστω  .Άν υπάρχει μικρότερη τιμή για το
.Άν υπάρχει μικρότερη τιμή για το  απ΄αυτή της πρώτης περίπτωσης θα είναι
απ΄αυτή της πρώτης περίπτωσης θα είναι  .Οπότε έχουμε
.Οπότε έχουμε  .
. είναι
είναι  άτοπο.
άτοπο.
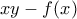 διατρέχει όλο το
διατρέχει όλο το  για τις διάφορες τιμές του
για τις διάφορες τιμές του  και θα το δεις μόνος σου.
και θα το δεις μόνος σου.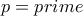 και
και  τότε θα πρέπει:
τότε θα πρέπει:
 η
η  .
. τότε
τότε  δεινή
δεινή  .
.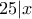 τότε
τότε  .
. αφού
αφού 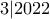 ,
, ,
, ,
, ,
, .
.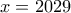 μπορούμε να πάρουμε
μπορούμε να πάρουμε 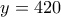 .
.