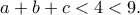Η διχοτόμος της γωνίας
 οξυγωνίου τριγώνου
οξυγωνίου τριγώνου  τέμνει την πλευρά
τέμνει την πλευρά  στο
στο 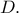 Ο περιγεγραμμένος κύκλος του τριγώνου
Ο περιγεγραμμένος κύκλος του τριγώνου  τέμνει την πλευρά
τέμνει την πλευρά  στα σημεία
στα σημεία  και
και 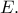 Η παράλληλη στην
Η παράλληλη στην  από το
από το  τέμνει την
τέμνει την  στο
στο 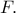 Να δείξετε ότι το τρίγωνο
Να δείξετε ότι το τρίγωνο  είναι ισοσκελές.
είναι ισοσκελές. ΘΕΜΑ 2
Να βρείτε το μικρότερο θετικό ακέραιο που μπορεί να γραφεί στη μορφή
 όπου
όπου  θετικοί ακέραιοι.
θετικοί ακέραιοι. ΘΕΜΑ 3
Οι θετικοί πραγματικοί αριθμοί
 ,
, ,
, ικανοποιούν τη σχέση
ικανοποιούν τη σχέση  Να δείξετε ότι
Να δείξετε ότι 
ΘΕΜΑ 4
Με πόσους τρόπους μπορούμε να τοποθετήσουμε στη σειρά
 βόλους, αν κάθε βόλος είναι είτε κόκκινος είτε πράσινος και δεν υπάρχουν πράσινοι βόλοι σε διαδοχικές θέσεις;
βόλους, αν κάθε βόλος είναι είτε κόκκινος είτε πράσινος και δεν υπάρχουν πράσινοι βόλοι σε διαδοχικές θέσεις;
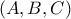 στο
στο  .Είναι
.Είναι  άρα
άρα  συνευθειακά και συνεπώς
συνευθειακά και συνεπώς  δηλαδή
δηλαδή  το μέσο του τόξου
το μέσο του τόξου 
![4=a+b+c+abc\geq 3\sqrt[3]{abc}+abc 4=a+b+c+abc\geq 3\sqrt[3]{abc}+abc](/forum/ext/geomar/texintegr/latexrender/pictures/1b930e3f583d9c1fe92463ae02cb6d8a.png) .Αν ήταν
.Αν ήταν  οπότε
οπότε ![3\sqrt[3]{abc}+abc\geq 4 3\sqrt[3]{abc}+abc\geq 4](/forum/ext/geomar/texintegr/latexrender/pictures/74956f190f09585c80234e59c3e38b47.png) .Είναι λοιπόν
.Είναι λοιπόν  .
.
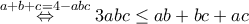
 αφού
αφού 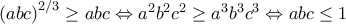 που ισχύει και η απόδειξη ολοκληρώθηκε.
που ισχύει και η απόδειξη ολοκληρώθηκε. παίρνομε τον αριθμό
παίρνομε τον αριθμό  ,θα δείξουμε ότι είναι και ο ζητούμενος.
,θα δείξουμε ότι είναι και ο ζητούμενος. φυσικοί ώστε
φυσικοί ώστε 
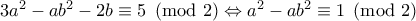
 άτοπο!
άτοπο!
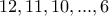 κόκκινους βόλους.
κόκκινους βόλους.  κόκκινους, θεωρούμε τη διάταξη
κόκκινους, θεωρούμε τη διάταξη 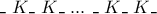 δηλαδή
δηλαδή  κενές θέσεις στα άκρα και ανάμεσά τους. Οι πράσινοι
κενές θέσεις στα άκρα και ανάμεσά τους. Οι πράσινοι  βόλοι μπορούν να τοποθετηθούν στις κενές θέσεις με
βόλοι μπορούν να τοποθετηθούν στις κενές θέσεις με  τρόπους.
τρόπους. τρόπο,
τρόπο,  τρόπους,
τρόπους,  τρόπους,
τρόπους,  τρόπους,
τρόπους,  τρόπους,
τρόπους,  τρόπους,
τρόπους,  τρόπους.
τρόπους.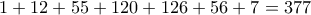 τρόποι.
τρόποι.
 . Θα δείξω την (*) με μόνη συνθήκη ότι
. Θα δείξω την (*) με μόνη συνθήκη ότι  . Έστω
. Έστω  και
και  με
με  και
και  ώστε
ώστε  .
.  , αφού
, αφού  με
με  και κυκλικά, οπότε αρκεί να δείξω ότι
και κυκλικά, οπότε αρκεί να δείξω ότι  .
. , άρα
, άρα  , καθώς
, καθώς 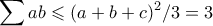 .
.![\dfrac{a}{b}+\dfrac{a}{c}+ab \geqslant \dfrac{3a}{\sqrt[3]{c}} \geqslant \dfrac{9a}{c+2} \dfrac{a}{b}+\dfrac{a}{c}+ab \geqslant \dfrac{3a}{\sqrt[3]{c}} \geqslant \dfrac{9a}{c+2}](/forum/ext/geomar/texintegr/latexrender/pictures/e3b8e9adf1df16bc462e56008b531da5.png) , και προσθέτοντας κυκλικά αρκεί να δείξουμε ότι
, και προσθέτοντας κυκλικά αρκεί να δείξουμε ότι  .
.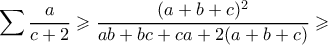
 , καθώς
, καθώς  οπότε
οπότε 
 γράφεται
γράφεται 
 ενώ από την συνθήκη είναι
ενώ από την συνθήκη είναι