Αρχιμήδης 2020
Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5561
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
Re: Αρχιμήδης 2020
Συγχαρητήρια σε όλους τους επιτυχόντες αλλά και σε όλους, όσοι συμμετείχαν !
Καλή συνέχεια στον Προκριματικό !!!
Καλή συνέχεια στον Προκριματικό !!!
Λέξεις Κλειδιά:
- Al.Koutsouridis
- Δημοσιεύσεις: 1806
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Re: Αρχιμήδης 2020
Προβλημα 1 (Μικρών) Να λύσετε στους πραγματικούς αριθμούς την ανίσωση:
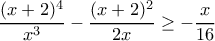 .
.
Λύση:
Φέρνοντας τους όρους σε κοινό παρονομαστή και στο αριστερό μέλος η ανίσωση γράφεται ισοδύναμα

Ο αριθμητής όμως του παραπάνω κλάσματος από της ανισότητα αριθμητικού γεωμετρικού μέσου για τους μη αρνητικούς αριθμούς προκύπτει να είναι μη αρνητικός για όλα τα
προκύπτει να είναι μη αρνητικός για όλα τα  . Επομένως το πρόσημο της ανίσωσης εξαρτάται από το πρόσημο του
. Επομένως το πρόσημο της ανίσωσης εξαρτάται από το πρόσημο του  . Άρα επαληθεύεται για όλα τα
. Άρα επαληθεύεται για όλα τα 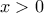 .
.
Edit: (βλέπε σε παρακάτω δημοσίευση) Στην περίπτωση που μηδενίζεται ο παρονομαστής δηλαδή για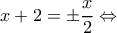
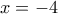 ή
ή 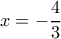 προκύπτουν άλλα δυο σημεία που επαληθεύουν την ανίσωση, ανεξάρτητα του προσήμου του
προκύπτουν άλλα δυο σημεία που επαληθεύουν την ανίσωση, ανεξάρτητα του προσήμου του  .
.
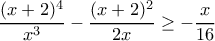 .
.Λύση:
Φέρνοντας τους όρους σε κοινό παρονομαστή και στο αριστερό μέλος η ανίσωση γράφεται ισοδύναμα

Ο αριθμητής όμως του παραπάνω κλάσματος από της ανισότητα αριθμητικού γεωμετρικού μέσου για τους μη αρνητικούς αριθμούς
 προκύπτει να είναι μη αρνητικός για όλα τα
προκύπτει να είναι μη αρνητικός για όλα τα  . Επομένως το πρόσημο της ανίσωσης εξαρτάται από το πρόσημο του
. Επομένως το πρόσημο της ανίσωσης εξαρτάται από το πρόσημο του  . Άρα επαληθεύεται για όλα τα
. Άρα επαληθεύεται για όλα τα 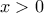 .
.Edit: (βλέπε σε παρακάτω δημοσίευση) Στην περίπτωση που μηδενίζεται ο παρονομαστής δηλαδή για
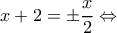
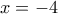 ή
ή 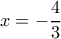 προκύπτουν άλλα δυο σημεία που επαληθεύουν την ανίσωση, ανεξάρτητα του προσήμου του
προκύπτουν άλλα δυο σημεία που επαληθεύουν την ανίσωση, ανεξάρτητα του προσήμου του  .
.
τελευταία επεξεργασία από Al.Koutsouridis σε Σάβ Φεβ 22, 2020 11:47 pm, έχει επεξεργασθεί 1 φορά συνολικά.
-
Τσιαλας Νικολαος
- Δημοσιεύσεις: 789
- Εγγραφή: Σάβ Ιαν 17, 2015 1:04 pm
Re: Αρχιμήδης 2020
Κύριε Αλέξανδρε σε αυτό την πάτησαν αρκετά παιδιά! Όταν ο αριθμητής είναι ίσος με το μηδέν, ο παρονομαστής μπορεί να είναι και αρνητικός! Οπότε έχουμε και 2 αρνητικές λύσεις!
- Al.Koutsouridis
- Δημοσιεύσεις: 1806
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Re: Αρχιμήδης 2020
Σωστά η περίπτωση μηδενισμού του παρονομαστή πρέπει να εξεταστεί ξεχωριστά. (δε χρειάζεται το κύριοςΤσιαλας Νικολαος έγραψε: ↑Σάβ Φεβ 22, 2020 11:23 pmΚύριε Αλέξανδρε σε αυτό την πάτησαν αρκετά παιδιά! Όταν ο αριθμητής είναι ίσος με το μηδέν, ο παρονομαστής μπορεί να είναι και αρνητικός! Οπότε έχουμε και 2 αρνητικές λύσεις!
Re: Αρχιμήδης 2020
Γραφική επιβεβαίωση... 
https://www.desmos.com/calculator/rus3gvvkcw
https://www.desmos.com/calculator/rus3gvvkcw
Τσιαλας Νικολαος έγραψε: ↑Σάβ Φεβ 22, 2020 11:23 pmΚύριε Αλέξανδρε σε αυτό την πάτησαν αρκετά παιδιά! Όταν ο αριθμητής είναι ίσος με το μηδέν, ο παρονομαστής μπορεί να είναι και αρνητικός! Οπότε έχουμε και 2 αρνητικές λύσεις!
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13298
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
-
Κώστας Καρ.
- Δημοσιεύσεις: 7
- Εγγραφή: Πέμ Ιαν 24, 2019 10:17 pm
Re: Αρχιμήδης 2020
Καλημερα σε ολους και συγχαρητηρια στους επιτυχοντες και σε ολους τους συμμετεχοντες
Μηπως θα μπορουσε καποιος να ανεβασει μια λυση για το 4ο των μεγαλων ; Νομιζω οτι διαφερει λιγο με την κλασικη θεωρια αριθμων που συνηθιζαν να βαζουν στον αρχιμηδη.
Μηπως θα μπορουσε καποιος να ανεβασει μια λυση για το 4ο των μεγαλων ; Νομιζω οτι διαφερει λιγο με την κλασικη θεωρια αριθμων που συνηθιζαν να βαζουν στον αρχιμηδη.
Re: Αρχιμήδης 2020
Συγχαρητήρια στους μαθητείες όλους που συμμετείχαν στο διαγωνισμό καλή συνέχεια στους διακριθέντες .
Γεωμετρία των μεγάλων μια λύση .
Ας είναι το μέσο του
το μέσο του  και
και  το σημείο τομής των καθέτων ευθειών
το σημείο τομής των καθέτων ευθειών  . Θέτω
. Θέτω 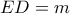 και θα είναι :
και θα είναι :
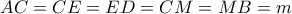 . Άρα το τετράπλευρο
. Άρα το τετράπλευρο 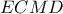 είναι ρόμβος ,το τρίγωνο
είναι ρόμβος ,το τρίγωνο  ορθογώνιο στο
ορθογώνιο στο  και το τετράπλευρο
και το τετράπλευρο 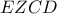 ισοσκελές τραπέζιο .
ισοσκελές τραπέζιο .
Τώρα το τετράπλευρο είναι εγγράψιμο γιατί το
είναι εγγράψιμο γιατί το  απέχει από τις κορυφές του απόσταση
απέχει από τις κορυφές του απόσταση  .
.
Είναι προφανές ότι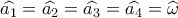 ( οξείες με πλευρές κάθετες )
( οξείες με πλευρές κάθετες )
Επίσης :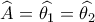 ( συμπληρώματα της
( συμπληρώματα της 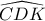 )
)
Μα τώρα το τρίγωνο είναι όμοιο με το τρίγωνο
είναι όμοιο με το τρίγωνο  ( αλλά και με όλα τα ισοσκελή τρίγωνα που έχουν τη μια γωνία
( αλλά και με όλα τα ισοσκελή τρίγωνα που έχουν τη μια γωνία  και την άλλη
και την άλλη 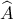 )
)
Το τρίγωνο λοιπόν είναι ισοσκελές με κορυφή το
είναι ισοσκελές με κορυφή το  και θα έχει φορέα της διχοτόμου της κορυφής του την
και θα έχει φορέα της διχοτόμου της κορυφής του την 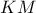 .
.
Είναι δε προφανές ότι κάθε γωνία ίση με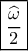 θα είναι ίση με την
θα είναι ίση με την 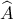 . Δηλαδή :
. Δηλαδή :
 αλλά επειδή στο ισοσκελές τραπέζιο
αλλά επειδή στο ισοσκελές τραπέζιο 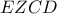 οι διαγώνιες είναι ίσες
οι διαγώνιες είναι ίσες
Η είναι μεσοκάθετη στο
είναι μεσοκάθετη στο 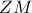 άρα
άρα 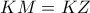 και λόγω της
και λόγω της  θα είναι και
θα είναι και
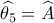 , κι αφού το τρίγωνο
, κι αφού το τρίγωνο  είναι ισοσκελές με κορυφή το
είναι ισοσκελές με κορυφή το  οι
οι
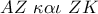 είναι αντικείμενες ημιευθείες .
είναι αντικείμενες ημιευθείες .
Γεωμετρία των μεγάλων μια λύση .
Ας είναι
 το μέσο του
το μέσο του  και
και  το σημείο τομής των καθέτων ευθειών
το σημείο τομής των καθέτων ευθειών  . Θέτω
. Θέτω 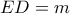 και θα είναι :
και θα είναι :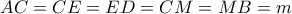 . Άρα το τετράπλευρο
. Άρα το τετράπλευρο 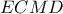 είναι ρόμβος ,το τρίγωνο
είναι ρόμβος ,το τρίγωνο  ορθογώνιο στο
ορθογώνιο στο  και το τετράπλευρο
και το τετράπλευρο 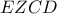 ισοσκελές τραπέζιο .
ισοσκελές τραπέζιο .Τώρα το τετράπλευρο
 είναι εγγράψιμο γιατί το
είναι εγγράψιμο γιατί το  απέχει από τις κορυφές του απόσταση
απέχει από τις κορυφές του απόσταση  .
. Είναι προφανές ότι
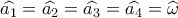 ( οξείες με πλευρές κάθετες )
( οξείες με πλευρές κάθετες )Επίσης :
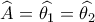 ( συμπληρώματα της
( συμπληρώματα της 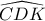 )
) Μα τώρα το τρίγωνο
 είναι όμοιο με το τρίγωνο
είναι όμοιο με το τρίγωνο  ( αλλά και με όλα τα ισοσκελή τρίγωνα που έχουν τη μια γωνία
( αλλά και με όλα τα ισοσκελή τρίγωνα που έχουν τη μια γωνία  και την άλλη
και την άλλη 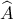 )
)Το τρίγωνο λοιπόν
 είναι ισοσκελές με κορυφή το
είναι ισοσκελές με κορυφή το  και θα έχει φορέα της διχοτόμου της κορυφής του την
και θα έχει φορέα της διχοτόμου της κορυφής του την 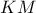 .
.Είναι δε προφανές ότι κάθε γωνία ίση με
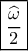 θα είναι ίση με την
θα είναι ίση με την 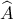 . Δηλαδή :
. Δηλαδή : αλλά επειδή στο ισοσκελές τραπέζιο
αλλά επειδή στο ισοσκελές τραπέζιο 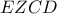 οι διαγώνιες είναι ίσες
οι διαγώνιες είναι ίσες Η
 είναι μεσοκάθετη στο
είναι μεσοκάθετη στο 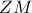 άρα
άρα 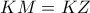 και λόγω της
και λόγω της  θα είναι και
θα είναι και 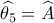 , κι αφού το τρίγωνο
, κι αφού το τρίγωνο  είναι ισοσκελές με κορυφή το
είναι ισοσκελές με κορυφή το  οι
οι 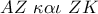 είναι αντικείμενες ημιευθείες .
είναι αντικείμενες ημιευθείες .
τελευταία επεξεργασία από Doloros σε Κυρ Φεβ 23, 2020 11:55 am, έχει επεξεργασθεί 1 φορά συνολικά.
Re: Αρχιμήδης 2020
Πολλά συγχαρητήρια σε όλους τους μαθητές και καλή επιτυχία στον προκριματικό!
Παραθέτω αρχικά μια λύση στο θέμα 4 των μεγάλων που βλέπω πως δεν έχει απαντηθεί, μαζί με τον τρόπο σκέψης:
Σαν πρώτο βήμα, κοιτάμε να βρούμε θετικούς ακέραιους για τους οποίους το
για τους οποίους το 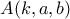 μπορεί να είναι σύνθετος θετικός ακέραιος για
μπορεί να είναι σύνθετος θετικός ακέραιος για 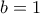 . Με αυτό τον τρόπο οδηγούμαστε σε ένα πιο απλό πρόβλημα, το οποίο αν λύσουμε θα έχουμε αποκλείσει μερικούς
. Με αυτό τον τρόπο οδηγούμαστε σε ένα πιο απλό πρόβλημα, το οποίο αν λύσουμε θα έχουμε αποκλείσει μερικούς  , το οποίο είναι σαφώς μια πρόοδος.
, το οποίο είναι σαφώς μια πρόοδος.
Θέλουμε λοιπόν σε πρώτη φάση: και το πηλίκο να είναι σύνθετος θετικός ακέραιος. Αυτό επιτυγχάνεται αν έχουμε
και το πηλίκο να είναι σύνθετος θετικός ακέραιος. Αυτό επιτυγχάνεται αν έχουμε  και συγχρόνως ο
και συγχρόνως ο 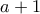 είναι σύνθετος. Εύκολα, η
είναι σύνθετος. Εύκολα, η  ικανοποιείται αν
ικανοποιείται αν 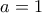 , αλλά τότε
, αλλά τότε  που είναι πρώτος, οπότε θέλουμε κάτι άλλο. Επειδή όμως η
που είναι πρώτος, οπότε θέλουμε κάτι άλλο. Επειδή όμως η  είναι δευτεροβάθμια ως προς
είναι δευτεροβάθμια ως προς  , ικανοποιείται και για
, ικανοποιείται και για 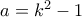 που είναι θετικός ακέραιος αν
που είναι θετικός ακέραιος αν  , και σε αυτή την περίπτωση έχουμε
, και σε αυτή την περίπτωση έχουμε 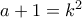 που είναι σύνθετος θετικός ακέραιος. Καταφέραμε λοιπόν να αποκλείσουμε όλους τους
που είναι σύνθετος θετικός ακέραιος. Καταφέραμε λοιπόν να αποκλείσουμε όλους τους  .
.
Αρκεί τώρα να δούμε τι γίνεται για . Χωρίς βλάβη της γενικότητας έχουμε
. Χωρίς βλάβη της γενικότητας έχουμε 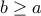 , και αν
, και αν 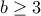 έχουμε:
έχουμε:
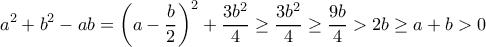
οπότε το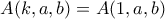 δεν μπορεί να είναι ακέραιος.
δεν μπορεί να είναι ακέραιος.
Άρα μένουν οι περιπτώσεις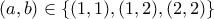 , στις οποίες εύκολα διαπιστώνουμε πως ο
, στις οποίες εύκολα διαπιστώνουμε πως ο 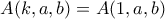 είναι ίσος είτε με
είναι ίσος είτε με  είτε με
είτε με  , δηλαδή μη σύνθετος θετικός ακέραιος.
, δηλαδή μη σύνθετος θετικός ακέραιος.
Άρα μόνο ο έχει τη ζητούμενη ιδιότητα.
έχει τη ζητούμενη ιδιότητα.
Κλείνω τώρα με ένα εναλλακτικό τελείωμα της γεωμετρίας των μεγάλων (θέμα 2 μεγάλων):
Αλλάζοντας ελαφρώς το σχήμα του Doloros στην αμέσως προηγούμενη ανάρτηση, ονομάζουμε την τομή των
την τομή των  και
και  και
και 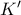 την τομή της
την τομή της  με την κάθετη από το
με την κάθετη από το  στην
στην  . Αρκεί να δείξουμε ότι
. Αρκεί να δείξουμε ότι  . Το τετράπλευρο
. Το τετράπλευρο  είναι και αυτό ισοσκελές τραπέζιο, άρα εγγράψιμο σε κύκλο, και θα δείξουμε πως το κέντρο του κύκλου αυτού είναι το μέσο
είναι και αυτό ισοσκελές τραπέζιο, άρα εγγράψιμο σε κύκλο, και θα δείξουμε πως το κέντρο του κύκλου αυτού είναι το μέσο  της
της 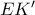 . Πράγματι, έχουμε
. Πράγματι, έχουμε 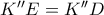 με
με  ,
,  ,
,  συνευθειακά (αφού
συνευθειακά (αφού  ). Επειδή το
). Επειδή το  είναι ρόμβος, η
είναι ρόμβος, η  είναι μεσοκάθετος της
είναι μεσοκάθετος της 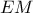 , άρα λόγω της παραπάνω συνευθειακότητας έχουμε και
, άρα λόγω της παραπάνω συνευθειακότητας έχουμε και  . Συνδυάζοντας τις τελευταίες ισότητες, έχουμε
. Συνδυάζοντας τις τελευταίες ισότητες, έχουμε 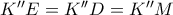 , οπότε πράγματι το
, οπότε πράγματι το  είναι το κέντρο του κύκλου του εγγράψιμου τραπεζίου
είναι το κέντρο του κύκλου του εγγράψιμου τραπεζίου  , επομένως έχουμε
, επομένως έχουμε 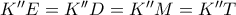 . Επειδή τώρα το τρίγωνο
. Επειδή τώρα το τρίγωνο 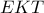 είναι ορθογώνιο και
είναι ορθογώνιο και 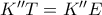 με
με  πάνω στην
πάνω στην  , το
, το  είναι μέσο της υποτείνουσας
είναι μέσο της υποτείνουσας  τριγώνου αυτού. Τέλος, αφού το
τριγώνου αυτού. Τέλος, αφού το  είναι μέσο και της
είναι μέσο και της 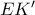 , έχουμε
, έχουμε  και η απόδειξη ολοκληρώθηκε.
και η απόδειξη ολοκληρώθηκε.
Παραθέτω αρχικά μια λύση στο θέμα 4 των μεγάλων που βλέπω πως δεν έχει απαντηθεί, μαζί με τον τρόπο σκέψης:
Σαν πρώτο βήμα, κοιτάμε να βρούμε θετικούς ακέραιους
 για τους οποίους το
για τους οποίους το 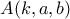 μπορεί να είναι σύνθετος θετικός ακέραιος για
μπορεί να είναι σύνθετος θετικός ακέραιος για 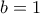 . Με αυτό τον τρόπο οδηγούμαστε σε ένα πιο απλό πρόβλημα, το οποίο αν λύσουμε θα έχουμε αποκλείσει μερικούς
. Με αυτό τον τρόπο οδηγούμαστε σε ένα πιο απλό πρόβλημα, το οποίο αν λύσουμε θα έχουμε αποκλείσει μερικούς  , το οποίο είναι σαφώς μια πρόοδος.
, το οποίο είναι σαφώς μια πρόοδος. Θέλουμε λοιπόν σε πρώτη φάση:
 και το πηλίκο να είναι σύνθετος θετικός ακέραιος. Αυτό επιτυγχάνεται αν έχουμε
και το πηλίκο να είναι σύνθετος θετικός ακέραιος. Αυτό επιτυγχάνεται αν έχουμε  και συγχρόνως ο
και συγχρόνως ο 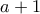 είναι σύνθετος. Εύκολα, η
είναι σύνθετος. Εύκολα, η  ικανοποιείται αν
ικανοποιείται αν 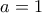 , αλλά τότε
, αλλά τότε  που είναι πρώτος, οπότε θέλουμε κάτι άλλο. Επειδή όμως η
που είναι πρώτος, οπότε θέλουμε κάτι άλλο. Επειδή όμως η  είναι δευτεροβάθμια ως προς
είναι δευτεροβάθμια ως προς  , ικανοποιείται και για
, ικανοποιείται και για 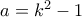 που είναι θετικός ακέραιος αν
που είναι θετικός ακέραιος αν  , και σε αυτή την περίπτωση έχουμε
, και σε αυτή την περίπτωση έχουμε 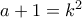 που είναι σύνθετος θετικός ακέραιος. Καταφέραμε λοιπόν να αποκλείσουμε όλους τους
που είναι σύνθετος θετικός ακέραιος. Καταφέραμε λοιπόν να αποκλείσουμε όλους τους  .
.Αρκεί τώρα να δούμε τι γίνεται για
 . Χωρίς βλάβη της γενικότητας έχουμε
. Χωρίς βλάβη της γενικότητας έχουμε 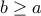 , και αν
, και αν 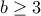 έχουμε:
έχουμε: 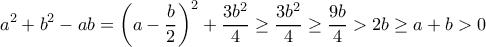
οπότε το
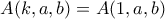 δεν μπορεί να είναι ακέραιος.
δεν μπορεί να είναι ακέραιος. Άρα μένουν οι περιπτώσεις
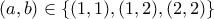 , στις οποίες εύκολα διαπιστώνουμε πως ο
, στις οποίες εύκολα διαπιστώνουμε πως ο 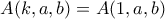 είναι ίσος είτε με
είναι ίσος είτε με  είτε με
είτε με  , δηλαδή μη σύνθετος θετικός ακέραιος.
, δηλαδή μη σύνθετος θετικός ακέραιος. Άρα μόνο ο
 έχει τη ζητούμενη ιδιότητα.
έχει τη ζητούμενη ιδιότητα.Κλείνω τώρα με ένα εναλλακτικό τελείωμα της γεωμετρίας των μεγάλων (θέμα 2 μεγάλων):
Αλλάζοντας ελαφρώς το σχήμα του Doloros στην αμέσως προηγούμενη ανάρτηση, ονομάζουμε
 την τομή των
την τομή των  και
και  και
και 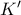 την τομή της
την τομή της  με την κάθετη από το
με την κάθετη από το  στην
στην  . Αρκεί να δείξουμε ότι
. Αρκεί να δείξουμε ότι  . Το τετράπλευρο
. Το τετράπλευρο  είναι και αυτό ισοσκελές τραπέζιο, άρα εγγράψιμο σε κύκλο, και θα δείξουμε πως το κέντρο του κύκλου αυτού είναι το μέσο
είναι και αυτό ισοσκελές τραπέζιο, άρα εγγράψιμο σε κύκλο, και θα δείξουμε πως το κέντρο του κύκλου αυτού είναι το μέσο  της
της 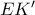 . Πράγματι, έχουμε
. Πράγματι, έχουμε 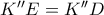 με
με  ,
,  ,
,  συνευθειακά (αφού
συνευθειακά (αφού  ). Επειδή το
). Επειδή το  είναι ρόμβος, η
είναι ρόμβος, η  είναι μεσοκάθετος της
είναι μεσοκάθετος της 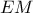 , άρα λόγω της παραπάνω συνευθειακότητας έχουμε και
, άρα λόγω της παραπάνω συνευθειακότητας έχουμε και  . Συνδυάζοντας τις τελευταίες ισότητες, έχουμε
. Συνδυάζοντας τις τελευταίες ισότητες, έχουμε 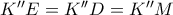 , οπότε πράγματι το
, οπότε πράγματι το  είναι το κέντρο του κύκλου του εγγράψιμου τραπεζίου
είναι το κέντρο του κύκλου του εγγράψιμου τραπεζίου  , επομένως έχουμε
, επομένως έχουμε 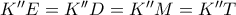 . Επειδή τώρα το τρίγωνο
. Επειδή τώρα το τρίγωνο 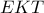 είναι ορθογώνιο και
είναι ορθογώνιο και 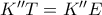 με
με  πάνω στην
πάνω στην  , το
, το  είναι μέσο της υποτείνουσας
είναι μέσο της υποτείνουσας  τριγώνου αυτού. Τέλος, αφού το
τριγώνου αυτού. Τέλος, αφού το  είναι μέσο και της
είναι μέσο και της 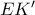 , έχουμε
, έχουμε  και η απόδειξη ολοκληρώθηκε.
και η απόδειξη ολοκληρώθηκε.
τελευταία επεξεργασία από Nick1990 σε Κυρ Φεβ 23, 2020 1:57 pm, έχει επεξεργασθεί 5 φορές συνολικά.
Κολλιοπουλος Νικος.
Μεταδιδακτορικός ερευνητής.
Ερευνητικά ενδιαφέροντα: Στοχαστικές ΜΔΕ, ασυμπτωτική ανάλυση στοχαστικών συστημάτων, εφαρμογές αυτών στα χρηματοοικονομικά και στη διαχείριση ρίσκων.
Μεταδιδακτορικός ερευνητής.
Ερευνητικά ενδιαφέροντα: Στοχαστικές ΜΔΕ, ασυμπτωτική ανάλυση στοχαστικών συστημάτων, εφαρμογές αυτών στα χρηματοοικονομικά και στη διαχείριση ρίσκων.
Re: Αρχιμήδης 2020
Γεωμετρία μικρών .
Το ημικύκλιο με διάμετρο το διέρχεται από τα σημεία
διέρχεται από τα σημεία  .
.
Ταυτόχρονα έχω :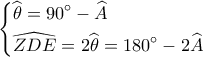
Αλλά οι ίσες γωνίες είναι μαζί
είναι μαζί  άρα :
άρα : 
Προφανώς και
και 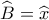 άρα :
άρα : 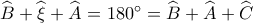
Συνεπώς : .
.
Επειδή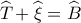 ( εξωτερική στο
( εξωτερική στο 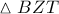 ) , θα είναι
) , θα είναι 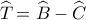
Τέλος
Το ημικύκλιο με διάμετρο το
 διέρχεται από τα σημεία
διέρχεται από τα σημεία  .
.Ταυτόχρονα έχω :
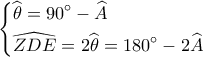
Αλλά οι ίσες γωνίες
 είναι μαζί
είναι μαζί  άρα :
άρα : 
Προφανώς
 και
και 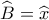 άρα :
άρα : 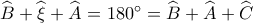
Συνεπώς :
 .
.Επειδή
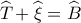 ( εξωτερική στο
( εξωτερική στο 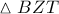 ) , θα είναι
) , θα είναι 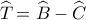
Τέλος

Re: Αρχιμήδης 2020
Για το πρόβλημα 4 των μικρών.
Α) Κάθε κύκλος μπορεί να χρωματιστεί κόκκινος ή πράσινος, άρα δυο επιλογές ανά κύκλο, συνολικά για τους 99 κύκλους έχω διαφορετικούς χρωματισμούς.
διαφορετικούς χρωματισμούς.
Β) αν στους πρώτους 50 κύκλους έχουμε Κ1 κόκκινους κύκλους, Π1 πράσινους κύκλους, στους υπόλοιπους 49 έχουμε Κ2 κόκκινους κύκλους, Π2 πράσινους κύκλους, τότε το Κ1 παίρνει τιμές από 0..50, το Κ2 από 0…49, Κ1+Π1=50, Κ2+Π2=49, και φυσικά ο χρωματισμός είναι «καλός» αν Κ1>Κ2. Δημιουργώ το εξής γράφημα καταστάσεων. Ο κατακόρυφος άξονας δηλώνει το πλήθος των κόκκινων κύκλων στους πρώτους 50 κύκλους (από τον 1 ως και τον 50ο), ενώ ο οριζόντιος άξονας Κ2 δηλώνει το πλήθος των κόκκινων κύκλων στους υπόλοιπους 49 (από τον 51 ως και τον 99ο).
Στη διαγώνιο με τα κυκλάκια (Ο) έχουμε Κ1=Κ2.
Όσα βρίσκονται πάνω από τη διαγώνιο με τα κυκλάκια (Ο), τα συμβολίζουμε με αστερίσκο (*) και έχουν συντεταγμένες (Κ2, Κ1) τέτοιες, ώστε , συνεπώς οι χρωματισμοί που αντιστοιχούν σε αυτόν τον συνδυασμό (Κ2,Κ1) είναι «καλοί».
, συνεπώς οι χρωματισμοί που αντιστοιχούν σε αυτόν τον συνδυασμό (Κ2,Κ1) είναι «καλοί».
Όσα βρίσκονται από τη διαγώνιο και κάτω τα συμβολίζουμε με κυκλάκια (Ο) και έχουν συντεταγμένες (Κ2, Κ1) τέτοιες, ώστε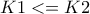 , συνεπώς οι χρωματισμοί που αντιστοιχούν σε αυτόν τον συνδυασμό (Κ2,Κ1) είναι «κακοί».
, συνεπώς οι χρωματισμοί που αντιστοιχούν σε αυτόν τον συνδυασμό (Κ2,Κ1) είναι «κακοί».
Σε κάθε αστεράκι (*) με συν/νες (Κ2,Κ1) θα αντιστοιχώ ένα κυκλάκι (Ο) με συντ/νες (49-Κ2, 50-Κ1) βλέπε και τα αντίστοιχα χρωματιστά ζευγάρια στην εικόνα.
Ένα κυκλάκι (Ο) με συντ/νές (49-Κ2, 50-Κ1) σημαίνει ότι έχουμε 49-Κ2 κόκκινους κύκλους στο 2ο τμήμα (από τον 51 ως και τον 99ο) και 50-Κ1 κόκκινους κύκλους στο 1ο τμήμα (από τον 1 ως και τον 50ο).
Αλλά τότε έχουμε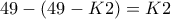 πράσινους κύκλους στο 2ο τμήμα (από τον 51 ως και τον 99ο) και
πράσινους κύκλους στο 2ο τμήμα (από τον 51 ως και τον 99ο) και 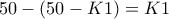 πράσινους κύκλους στο 1ο τμήμα (από τον 1 ως και τον 50ο).
πράσινους κύκλους στο 1ο τμήμα (από τον 1 ως και τον 50ο).
Όμως προφανώς οι χρωματισμοί που αντιστοιχούν σε αυτήν την περίπτωση είναι ισοπληθείς με τους αντίστοιχους χρωματισμούς για το αστεράκι με συν/νες (Κ2,Κ1),αρκεί να αντιστρέφω τα χρώματα!
Συνεπώς οι καλοί χρωματισμοί είναι ίσοι σε πλήθος με τους καλούς, άρα έχουμε διαφορετικούς καλούς χρωματισμούς
διαφορετικούς καλούς χρωματισμούς
Ελπίζω να μην σας μπέρδεψα.
Α) Κάθε κύκλος μπορεί να χρωματιστεί κόκκινος ή πράσινος, άρα δυο επιλογές ανά κύκλο, συνολικά για τους 99 κύκλους έχω
 διαφορετικούς χρωματισμούς.
διαφορετικούς χρωματισμούς.Β) αν στους πρώτους 50 κύκλους έχουμε Κ1 κόκκινους κύκλους, Π1 πράσινους κύκλους, στους υπόλοιπους 49 έχουμε Κ2 κόκκινους κύκλους, Π2 πράσινους κύκλους, τότε το Κ1 παίρνει τιμές από 0..50, το Κ2 από 0…49, Κ1+Π1=50, Κ2+Π2=49, και φυσικά ο χρωματισμός είναι «καλός» αν Κ1>Κ2. Δημιουργώ το εξής γράφημα καταστάσεων. Ο κατακόρυφος άξονας δηλώνει το πλήθος των κόκκινων κύκλων στους πρώτους 50 κύκλους (από τον 1 ως και τον 50ο), ενώ ο οριζόντιος άξονας Κ2 δηλώνει το πλήθος των κόκκινων κύκλων στους υπόλοιπους 49 (από τον 51 ως και τον 99ο).
Στη διαγώνιο με τα κυκλάκια (Ο) έχουμε Κ1=Κ2.
Όσα βρίσκονται πάνω από τη διαγώνιο με τα κυκλάκια (Ο), τα συμβολίζουμε με αστερίσκο (*) και έχουν συντεταγμένες (Κ2, Κ1) τέτοιες, ώστε
 , συνεπώς οι χρωματισμοί που αντιστοιχούν σε αυτόν τον συνδυασμό (Κ2,Κ1) είναι «καλοί».
, συνεπώς οι χρωματισμοί που αντιστοιχούν σε αυτόν τον συνδυασμό (Κ2,Κ1) είναι «καλοί».Όσα βρίσκονται από τη διαγώνιο και κάτω τα συμβολίζουμε με κυκλάκια (Ο) και έχουν συντεταγμένες (Κ2, Κ1) τέτοιες, ώστε
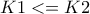 , συνεπώς οι χρωματισμοί που αντιστοιχούν σε αυτόν τον συνδυασμό (Κ2,Κ1) είναι «κακοί».
, συνεπώς οι χρωματισμοί που αντιστοιχούν σε αυτόν τον συνδυασμό (Κ2,Κ1) είναι «κακοί».Σε κάθε αστεράκι (*) με συν/νες (Κ2,Κ1) θα αντιστοιχώ ένα κυκλάκι (Ο) με συντ/νες (49-Κ2, 50-Κ1) βλέπε και τα αντίστοιχα χρωματιστά ζευγάρια στην εικόνα.
Ένα κυκλάκι (Ο) με συντ/νές (49-Κ2, 50-Κ1) σημαίνει ότι έχουμε 49-Κ2 κόκκινους κύκλους στο 2ο τμήμα (από τον 51 ως και τον 99ο) και 50-Κ1 κόκκινους κύκλους στο 1ο τμήμα (από τον 1 ως και τον 50ο).
Αλλά τότε έχουμε
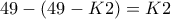 πράσινους κύκλους στο 2ο τμήμα (από τον 51 ως και τον 99ο) και
πράσινους κύκλους στο 2ο τμήμα (από τον 51 ως και τον 99ο) και 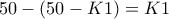 πράσινους κύκλους στο 1ο τμήμα (από τον 1 ως και τον 50ο).
πράσινους κύκλους στο 1ο τμήμα (από τον 1 ως και τον 50ο).Όμως προφανώς οι χρωματισμοί που αντιστοιχούν σε αυτήν την περίπτωση είναι ισοπληθείς με τους αντίστοιχους χρωματισμούς για το αστεράκι με συν/νες (Κ2,Κ1),αρκεί να αντιστρέφω τα χρώματα!
Συνεπώς οι καλοί χρωματισμοί είναι ίσοι σε πλήθος με τους καλούς, άρα έχουμε
 διαφορετικούς καλούς χρωματισμούς
διαφορετικούς καλούς χρωματισμούς Ελπίζω να μην σας μπέρδεψα.
Χρήστος Σαμουηλίδης
-
AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ
- Επιμελητής
- Δημοσιεύσεις: 1172
- Εγγραφή: Τετ Δεκ 31, 2008 8:07 pm
- Τοποθεσία: ΗΡΑΚΛΕΙΟ ΚΡΗΤΗΣ
Re: Αρχιμήδης 2020
Αφού συγχαρώ όλους τους εκπληκτικούς μαθητές μας, μία λύση για τη γεωμετρία των μεγάλων με σχήμα και χωρίς (σχεδόν) λόγια.
Τα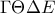 και
και  είναι ρόμβοι και καθώς το
είναι ρόμβοι και καθώς το 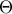 είναι ορθόκεντρο του ισοσκελούς τριγώνου
είναι ορθόκεντρο του ισοσκελούς τριγώνου  , η
, η 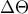 άρα και η
άρα και η 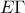 είναι κάθετες στην
είναι κάθετες στην 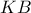 .
.
Τα
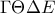 και
και  είναι ρόμβοι και καθώς το
είναι ρόμβοι και καθώς το 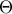 είναι ορθόκεντρο του ισοσκελούς τριγώνου
είναι ορθόκεντρο του ισοσκελούς τριγώνου  , η
, η 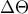 άρα και η
άρα και η 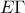 είναι κάθετες στην
είναι κάθετες στην 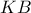 .
.- Συνημμένα
-
- geogebra-export.png (337.59 KiB) Προβλήθηκε 1993 φορές
-
socrates
- Επιμελητής
- Δημοσιεύσεις: 6461
- Εγγραφή: Δευ Μαρ 09, 2009 1:47 pm
- Τοποθεσία: Θεσσαλονίκη
- Επικοινωνία:
Re: Αρχιμήδης 2020
Πρόβλημα 1, Μεγάλοι
Belarus 2019
https://artofproblemsolving.com/communi ... 0p13060758
Πρόβλημα 4, Μεγάλοι
παρόμοιο
https://artofproblemsolving.com/communi ... 4p13415923
Πρόβλημα 4, Μικροί
θέμα 5
https://www.math.wisc.edu/talent/sites/ ... t18-2q.pdf
Πρόβλημα 2, Μικροί
Μάλλον πολύ απλό πρόβλημα για αυτό το επίπεδο. Δεν συνάδει με τα υπόλοιπα.
Belarus 2019
https://artofproblemsolving.com/communi ... 0p13060758
Πρόβλημα 4, Μεγάλοι
παρόμοιο
https://artofproblemsolving.com/communi ... 4p13415923
Πρόβλημα 4, Μικροί
θέμα 5
https://www.math.wisc.edu/talent/sites/ ... t18-2q.pdf
Πρόβλημα 2, Μικροί
Μάλλον πολύ απλό πρόβλημα για αυτό το επίπεδο. Δεν συνάδει με τα υπόλοιπα.
Θανάσης Κοντογεώργης
-
Τσιαλας Νικολαος
- Δημοσιεύσεις: 789
- Εγγραφή: Σάβ Ιαν 17, 2015 1:04 pm
Re: Αρχιμήδης 2020
Αναρτήθηκαν και οι επίσημες λύσεις!! Διακρίνω μια αλλαγή προς το καλύτερο αλλά θα προτιμούσα να έχει και κάποιους άλλους τρόπους που εμφανιστηκαν.
http://www.hms.gr/?q=node/1639
http://www.hms.gr/?q=node/1639
Re: Αρχιμήδης 2020
Καλησπέρα και συγχαρητήρια στους επιτυχόντες. Λογικά χάνω κάτια πολύ προφανές ή κανω κάποιο λάθος/παραδόχή, ελπίζω να μπορεί να με βοηθήσει κάποιος βρω τι κάνω λάθος. Αναφέρομαι στο υποερώτημα β) του τρίτου προβλήματος των μεγάλων:
Εφαρμόζω την κίνηση Κ (2,3),(4,5),...,(2020,2021) οπότε έχω 1010 ζεύγη και έτσι δημιουργώ 1010 μονάδες και αφού το 1010 είναι άρτιος οι μονάδες αυτές "φεύγουν" πάλι με την κίνηση Κ μεταξύ τους. Οπότε έχουν μείνει οι αριθμοί 1,2022,2023,2024,2025,2026,2027,2028,2029,2030. Εφαρμόζω τώρα την κίνηση Κ για τα ζεύγη: (2023,2024),(2025,2026),(2027,2028),(2029,2030) και σχηματίζονται άλλες 4 μονάδες οι οποίες φεύγουν πάλι με την κίνηση Κ αφου το 4 είναι άρτιος. Έτσι έχει μείνει το 2022 και το 1 οπότε εφαρμόζοντας και πάλι την κίνηση Κ παίρνω 2021^2020 οπότε γίνεται.
Εφαρμόζω την κίνηση Κ (2,3),(4,5),...,(2020,2021) οπότε έχω 1010 ζεύγη και έτσι δημιουργώ 1010 μονάδες και αφού το 1010 είναι άρτιος οι μονάδες αυτές "φεύγουν" πάλι με την κίνηση Κ μεταξύ τους. Οπότε έχουν μείνει οι αριθμοί 1,2022,2023,2024,2025,2026,2027,2028,2029,2030. Εφαρμόζω τώρα την κίνηση Κ για τα ζεύγη: (2023,2024),(2025,2026),(2027,2028),(2029,2030) και σχηματίζονται άλλες 4 μονάδες οι οποίες φεύγουν πάλι με την κίνηση Κ αφου το 4 είναι άρτιος. Έτσι έχει μείνει το 2022 και το 1 οπότε εφαρμόζοντας και πάλι την κίνηση Κ παίρνω 2021^2020 οπότε γίνεται.
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: Αρχιμήδης 2020
Οι μονάδες δεν φεύγουν, γίνονται μηδενικά.llenny έγραψε: ↑Τετ Φεβ 26, 2020 10:14 pmΚαλησπέρα και συγχαρητήρια στους επιτυχόντες. Λογικά χάνω κάτια πολύ προφανές ή κανω κάποιο λάθος/παραδόχή, ελπίζω να μπορεί να με βοηθήσει κάποιος βρω τι κάνω λάθος. Αναφέρομαι στο υποερώτημα β) του τρίτου προβλήματος των μεγάλων:
Εφαρμόζω την κίνηση Κ (2,3),(4,5),...,(2020,2021) οπότε έχω 1010 ζεύγη και έτσι δημιουργώ 1010 μονάδες και αφού το 1010 είναι άρτιος οι μονάδες αυτές "φεύγουν" πάλι με την κίνηση Κ μεταξύ τους. Οπότε έχουν μείνει οι αριθμοί 1,2022,2023,2024,2025,2026,2027,2028,2029,2030. Εφαρμόζω τώρα την κίνηση Κ για τα ζεύγη: (2023,2024),(2025,2026),(2027,2028),(2029,2030) και σχηματίζονται άλλες 4 μονάδες οι οποίες φεύγουν πάλι με την κίνηση Κ αφου το 4 είναι άρτιος. Έτσι έχει μείνει το 2022 και το 1 οπότε εφαρμόζοντας και πάλι την κίνηση Κ παίρνω 2021^2020 οπότε γίνεται.
Re: Αρχιμήδης 2020
Τα μηδενικά όμως δεν φεύγουν επίσης αφού εφαρμόζοντας την κίνηση Κ για τα μηδενικά και τους αριθμούς που μένουν, μένουν μόνο οι άλλοι αριθμοί;
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: Αρχιμήδης 2020
Όχι, μπορούν να φύγουν όλα εκτός από ένα. Στο τέλος θα σου μείνει  . (Τα μηδενικά αριστερά του
. (Τα μηδενικά αριστερά του  μπορούν να φύγουν όλα χρησιμοποιώντας το
μπορούν να φύγουν όλα χρησιμοποιώντας το  .)
.)
Τώρα είτε θα γίνει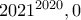 και μετά
και μετά 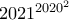 είτε
είτε 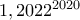 και μετά
και μετά  .
.
 . (Τα μηδενικά αριστερά του
. (Τα μηδενικά αριστερά του  μπορούν να φύγουν όλα χρησιμοποιώντας το
μπορούν να φύγουν όλα χρησιμοποιώντας το  .)
.)Τώρα είτε θα γίνει
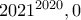 και μετά
και μετά 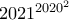 είτε
είτε 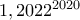 και μετά
και μετά  .
.Re: Αρχιμήδης 2020
Μπορούμε να προσδιορίσουμε όλους τους αριθμούς που είναι δυνατόν να μείνουν στο τέλος στο πρόβλημα 3 των μεγάλων;
Σιλουανός Μπραζιτίκος
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 16 επισκέπτες
