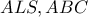2η μέρα: Θέματα της 3ης φάσης για την 9η τάξη.
1. Ο Πέτρος και ο Μιχάλης ξεκινούν από ένα σημείο κυκλικής διαδρομής με κατεύθυνση αντίθετη της φοράς των δεικτών του ρολογιού. Και οι δυο τρέχουν με σταθερές ταχύτητες, η ταχύτητα του Μιχάλη είναι κατά
 % μεγαλύτερη του Πέτρου. Ο Πέτρος όλη την ώρα τρέχει αντίθετα με την φορά των δεικτών του ρολογιού, αλλά ο Μιχάλης μπορεί να αλλάξει την κατεύθυνση του τρεξίματος σε οποιαδήποτε στιγμή, αμέσως μετά από όταν έχει τρέξει ένα ημικύκλιο ή περισσότερο προς την μια κατεύθυνση. Να δείξετε, ότι ενόσω ο Πέτρος τρέχει τον πρώτο γύρο, ο Μιχάλης μπορεί να "εξισωθεί" (να συναντηθεί ή να τον φτάσει) μαζί του τρεις φορές, μη υπολογίζοντας την αρχική στιγμή.
% μεγαλύτερη του Πέτρου. Ο Πέτρος όλη την ώρα τρέχει αντίθετα με την φορά των δεικτών του ρολογιού, αλλά ο Μιχάλης μπορεί να αλλάξει την κατεύθυνση του τρεξίματος σε οποιαδήποτε στιγμή, αμέσως μετά από όταν έχει τρέξει ένα ημικύκλιο ή περισσότερο προς την μια κατεύθυνση. Να δείξετε, ότι ενόσω ο Πέτρος τρέχει τον πρώτο γύρο, ο Μιχάλης μπορεί να "εξισωθεί" (να συναντηθεί ή να τον φτάσει) μαζί του τρεις φορές, μη υπολογίζοντας την αρχική στιγμή. 2. Ο πράσινος χαμαιλέοντας λέει πάντα την αλήθεια και ο καφέ χαμαιλέοντας ψεύδεται και μετά από αυτό κατευθείαν πρασινίζει. Σε μια ομάδα
 χαμαιλεόντων (πράσινων και καφέ) ο καθένας με την σειρά απάντησε στην ερώτηση, πόσοι μεταξύ αυτών τώρα είναι πράσινοι. Απαντήσεις ήταν οι αριθμοί
χαμαιλεόντων (πράσινων και καφέ) ο καθένας με την σειρά απάντησε στην ερώτηση, πόσοι μεταξύ αυτών τώρα είναι πράσινοι. Απαντήσεις ήταν οι αριθμοί  (με κάποια σειρά, εξάλλου όχι απαραίτητα με την υποδειχθείσα). Ποιος είναι ο μέγιστος αριθμός πράσινων χαμαιλεόντων που θα μπορούσαν να υπάρχουν αρχικά;
(με κάποια σειρά, εξάλλου όχι απαραίτητα με την υποδειχθείσα). Ποιος είναι ο μέγιστος αριθμός πράσινων χαμαιλεόντων που θα μπορούσαν να υπάρχουν αρχικά;3. Σε οξυγώνιο τρίγωνο
 φέρουμε την διχοτόμο
φέρουμε την διχοτόμο  . Ο περιγεγραμμένος κύκλος του τριγώνου
. Ο περιγεγραμμένος κύκλος του τριγώνου  τέμνει την πλευρά
τέμνει την πλευρά  στο σημείο
στο σημείο  . Προέκυψε ότι το σημείο
. Προέκυψε ότι το σημείο  , συμμετρικό του σημείου
, συμμετρικό του σημείου  ως προς την ευθεία
ως προς την ευθεία  , να βρίσκεται επί της πλευράς
, να βρίσκεται επί της πλευράς  και να μην συμπίπτει με τα άκρα της. Ποιες τιμές μπορεί να πάρει η γωνία
και να μην συμπίπτει με τα άκρα της. Ποιες τιμές μπορεί να πάρει η γωνία  ;
;4. Θα ονομάσουμε ένα πολύγωνο καλό αν σε αυτό βρεθεί ζεύγος παράλληλων πλευρών. Ένα κανονικό πολύγωνο διαμερίστηκε με μη τεμνόμενες (σε εσωτερικά σημεία) διαγώνιούς του σε κάμποσα πολύγωνα έτσι, ώστε όλα αυτά τα πολύγωνα να έχουν τον ίδιο περιττό αριθμό πλευρών. Μπορεί άραγε να προκύψει, ότι μεταξύ αυτών των πολυγώνων υπάρχει τουλάχιστον ένα καλό;
5. Να αποδείξετε, ότι για οποιουσδήποτε θετικούς αριθμούς
 ισχύει η ανισότητα
ισχύει η ανισότητα .
.
 το σημείο εκκίνησης και
το σημείο εκκίνησης και  το αντιδιαμετρικό του.Επειδή τρέχουν στον ίδιο κύκλο διαιρώντας τις γραμμικές του ταχύτητες με την ακτίνα του κύκλου η δοσμένη σχέση γίνεται σχέση γωνιακών ταχυτήτων και έστω χωρίς βλάβη ότι οι ταχύτητες σε μοίρες/sec είναι
το αντιδιαμετρικό του.Επειδή τρέχουν στον ίδιο κύκλο διαιρώντας τις γραμμικές του ταχύτητες με την ακτίνα του κύκλου η δοσμένη σχέση γίνεται σχέση γωνιακών ταχυτήτων και έστω χωρίς βλάβη ότι οι ταχύτητες σε μοίρες/sec είναι 
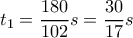 και ο Πέτρος έχει διαγράψει τόξο
και ο Πέτρος έχει διαγράψει τόξο  .Εκείνη την στιγμή ο Μιχάλης αλλάζει φορά και κινείται προς το
.Εκείνη την στιγμή ο Μιχάλης αλλάζει φορά και κινείται προς το  ,ενώ στην πορεία συναντά τον Μιχάλη για πρώτη φορά.
,ενώ στην πορεία συναντά τον Μιχάλη για πρώτη φορά. ο Μιχάλης έχει διανύσει άλλες
ο Μιχάλης έχει διανύσει άλλες  (έστω ότι βρίσκεται στο
(έστω ότι βρίσκεται στο  πιο κοντά στο
πιο κοντά στο  ο Μιχάλης έχει χρόνο ώστε απειροελάχιστα μετά την συνάντηση να αλλάξει φορά και να ξανα-εξισωθεί με τον Μιχάλη πριν αυτός τερματίσει τον πρώτο γύρο.
ο Μιχάλης έχει χρόνο ώστε απειροελάχιστα μετά την συνάντηση να αλλάξει φορά και να ξανα-εξισωθεί με τον Μιχάλη πριν αυτός τερματίσει τον πρώτο γύρο. , και
, και  .
.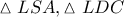 , είναι :
, είναι : , και αφού
, και αφού  από το εγγράψιμο
από το εγγράψιμο  , προκύπτει ότι
, προκύπτει ότι  ή
ή  .
. και
και  .
. Αν
Αν  .
. . Τότε όμως, θα είναι
. Τότε όμως, θα είναι  , άρα ο περιγεγραμμένος κύκλος του
, άρα ο περιγεγραμμένος κύκλος του  εφάπτεται στην
εφάπτεται στην  .
.
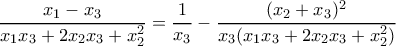 και οι κυκλικές αυτής).
και οι κυκλικές αυτής). .
. και οι κυκλικές αυτής.
και οι κυκλικές αυτής.![\displaystyle \sum \dfrac{(x_2+x_3)^2}{x_3(x_1x_3+2x_2x_3+x_2^2)} \leqslant \sum [\dfrac{x_2}{x_3(x_2+x_3)}+\dfrac{1}{x_1+x_2}]= \displaystyle \sum \dfrac{(x_2+x_3)^2}{x_3(x_1x_3+2x_2x_3+x_2^2)} \leqslant \sum [\dfrac{x_2}{x_3(x_2+x_3)}+\dfrac{1}{x_1+x_2}]=](/forum/ext/geomar/texintegr/latexrender/pictures/937b7eeac2bd8280fa139cd6022fa158.png)
![\displaystyle \sum [ \dfrac{x_1}{x_2(x_1+x_2)}+\dfrac{1}{x_1+x_2}]=\sum \dfrac{1}{x_2}=\sum \dfrac{1}{x_1} \displaystyle \sum [ \dfrac{x_1}{x_2(x_1+x_2)}+\dfrac{1}{x_1+x_2}]=\sum \dfrac{1}{x_2}=\sum \dfrac{1}{x_1}](/forum/ext/geomar/texintegr/latexrender/pictures/1666fada888238323913d23d0d84d3e4.png) , και η προς απόδειξη δείχθηκε.
, και η προς απόδειξη δείχθηκε. οι αρχικά πράσινοι χαμαιλέοντες και έστω
οι αρχικά πράσινοι χαμαιλέοντες και έστω  οι απαντήσεις τους με
οι απαντήσεις τους με  .Αυτό σημαίνει ότι απάντησε πρώτος ο
.Αυτό σημαίνει ότι απάντησε πρώτος ο 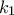 μετά ο
μετά ο  κλπ αφού για κάθε καφέ χαμαιλέοντα που απαντά ο αριθμός των πράσινων αυξάνει κατά
κλπ αφού για κάθε καφέ χαμαιλέοντα που απαντά ο αριθμός των πράσινων αυξάνει κατά  . Έτσι ανάμεσα σε κάθε 2 πράσινους χαμαιλέοντες υπάρχει τουλάχιστον
. Έτσι ανάμεσα σε κάθε 2 πράσινους χαμαιλέοντες υπάρχει τουλάχιστον 
 μπορεί να επιτευχθεί αν οι απαντήσεις είναι οι εξής :
μπορεί να επιτευχθεί αν οι απαντήσεις είναι οι εξής :  δηλαδή ξεκινάμε με πράσινο και τελειώνουμε σε πράσινο ενώ εναλλάξ υπάρχει και ένας καφέ (όλοι οι καφέ λένε ψέματα αφού
δηλαδή ξεκινάμε με πράσινο και τελειώνουμε σε πράσινο ενώ εναλλάξ υπάρχει και ένας καφέ (όλοι οι καφέ λένε ψέματα αφού  )
) και
και 
 είναι όμοια,
είναι όμοια,  οπότε και τα
οπότε και τα