Ανοιχτή Ολυμπιάδα ΦΜΛ 239 (10-11η τάξη, 2015)

Al.Koutsouridis · #1

Ανοιχτή Ολυμπιάδα Φυσικομαθηματικού Λυκείου 239 Αγίας Πετρούπολης για τις τάξεις 10η και 11η, 2015.

1. Ο εγγεγραμμένος κύκλος του τριγώνου ABC

εφάπτεται των πλευρών του AB,BC,CA

στα σημεία $C_{1}, A_{1}, B_{1}$ αντίστοιχα. Η ευθεία $A_{1}C_{1}$ τέμνει την παράλληλη από το σημείο

ως προς την πλευρά

, στο σημείο

. Να αποδείξετε, ότι $\angle KB_{1}A_{1}=90^0$ .

2. Να αποδείξετε, ότι ο $C^{n}_{k+n}$ μπορεί να αναπαρασταθεί στη μορφή γινομένου ανά δυο πρώτων μεταξύ τους παραγόντων $a_{1}a_{2} \ldots a_{n}$ , όπου ο $a_{j}$ είναι διαιρέτης του αριθμού k+j

.

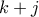3. Κάθε ακμή ενός γράφου

είναι χρωματισμένη με ένα από δυο χρώματα. Για καθένα από τα χρώματα όλες οι συνιστώσες συνεκτικότητας του γράφου, που αποτελούνται μόνο από το αυτό χρώμα, περιέχουν το πολύ n>1

κορυφές. Να αποδείξετε, ότι όλες οι κορυφές του γράφου

μπορούν να χρωματιστούν με

χρώματα με κανονικό τρόπο (

χρωματισμός).

4. Δίνεται ο θετικός ακέραιος

. Το πολυώνυμο f(x,y)

βαθμού το πολύ n-1

είναι τέτοιο, ώστε για οποιουσδήποτε θετικούς ακεραίους $x,y \leq n$ , $x+y \leq n+1$ , να ισχύει η ισότητα f(x,y)=x/y

. Να βρείτε το f(0,0)

.

5. Οι κόμβοι τρισδιάστατου μοναδιαίου κυβικού πλέγματος, όλες οι τρεις συντεταγμένες των οποίων είναι άρτιοι αριθμοί, χρωματίζονται με κόκκινο χρώμα και οι υπόλοιποι κόμβοι με μπλε. Δίνεται κυρτό πολύεδρο, όλες οι κορυφές του οποίου είναι κόκκινες. Το πλήθος των κόκκινων κόμβων στην επιφάνειά του το συμβολίζουμε με

. Πόσοι μπλε κόμβοι μπορεί να υπάρχουν στην επιφάνειά του;

6. Δίνονται οι θετικοί αριθμοί a,b,c

που ικανοποιούν την ισότητα

2a^3b+2b^3c+2c^3a=a^2b^2+b^2c^2+c^2a^2

.

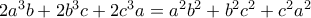Να αποδείξετε την ανισότητα

$2ab(a-b)^2+2bc(b-c)^2+2ca(c-a)^2 \geq (ab+bc+ca)^2$ .

7. Δυο μάγοι ετοιμάζονται να επιδείξουν το παρακάτω μαγικό. Στον πίνακα είναι σχεδιασμένος ένας κύκλος, στον οποίο είναι σημειωμένο ένα ημικύκλιο. Οι θεατές σημειώνουν σε αυτόν τον κύκλο 100

σημεία, ύστερα ο ένας μάγος σβήνει ένα από αυτά. Μετά από αυτό ο δεύτερος πρώτα κοιτάει το σχήμα και από τα εναπομείναντα

σημεία προσδιορίζει, αν το σβησμένο σημείο ανήκε στο σημειωμένο ημικύκλιο. Να αποδείξετε, ότι ένα τέτοιο κόλπο δεν είναι πάντα επιτυχές.

8. Σε ένα κύκλο επιλέχθηκαν 100

σημεία και για το καθένα από αυτά υπολογίστηκε το γινόμενο των αποστάσεων από τα υπόλοιπα. Μπορούν άραγε να προκύψουν οι αριθμοί από το

έως το

(με κάποια σειρά);

Πηγή

ΦΩΤΙΑΔΗΣ ΠΡΟΔΡΟΜΟΣ · #2

Al.Koutsouridis έγραψε: ↑
Τρί Ιαν 21, 2020 9:53 pm
Ανοιχτή Ολυμπιάδα Φυσικομαθηματικού Λυκείου 239 Αγίας Πετρούπολης για τις τάξεις 10η και 11η, 2015.

1. Ο εγγεγραμμένος κύκλος του τριγώνου εφάπτεται των πλευρών του στα σημεία $C_{1}, A_{1}, B_{1}$ αντίστοιχα. Η ευθεία $A_{1}C_{1}$ τέμνει την παράλληλη από το σημείο ως προς την πλευρά , στο σημείο . Να αποδείξετε, ότι $\angle KB_{1}A_{1}=90^0$ .

: 210.PNG (28.59 KiB) Προβλήθηκε 1498 φορές

Έστω

το έκκεντρο και $L\equiv B_1C_1\cap A_1I$ .Έστω

η τομή της KB_1

με τον έγκυκλο.
Το

ανήκει στην πολική του

άρα από La Hire το

είναι σημείο της πολικής του

η οποία θα είναι κάθετη στην

άρα παράλληλη στην

,δηλαδή η

.Το

λοιπόν ανήκει στην πολική του

άρα η πολική του

θα περνά από το

.Όμως ως γνωστών η πολική του

θα περνά από το σημείο τομής των A_1N,B_1C_1

, έτσι έχουμε ότι A_1,L,N

συνευθειακά και το ζητούμενο έπεται.

#3

Al.Koutsouridis έγραψε: ↑
Τρί Ιαν 21, 2020 9:53 pm
Ανοιχτή Ολυμπιάδα Φυσικομαθηματικού Λυκείου 239 Αγίας Πετρούπολης για τις τάξεις 10η και 11η, 2015.

1. Ο εγγεγραμμένος κύκλος του τριγώνου εφάπτεται των πλευρών του στα σημεία $C_{1}, A_{1}, B_{1}$ αντίστοιχα. Η ευθεία $A_{1}C_{1}$ τέμνει την παράλληλη από το σημείο ως προς την πλευρά , στο σημείο . Να αποδείξετε, ότι $\angle KB_{1}A_{1}=90^0$ .

Αλλιώς.

: ΦΜΛ 239 (2015).png (18.89 KiB) Προβλήθηκε 1436 φορές

$\displaystyle B{C_1} = B{A_1} \Rightarrow AK = A{C_1} = A{B_1} \Rightarrow A\widehat KB_1 = A\widehat {{B_1}}K$

$\displaystyle K\widehat A{B_1} = \widehat B + \widehat A = 180^\circ - \widehat C=A_1\widehat IB_1,$ άρα όλες οι κόκκινες

γωνίες είναι ίσες κι επειδή $\displaystyle I\widehat {{B_1}}A = 90^\circ \Rightarrow$ $\boxed{K\widehat {{B_1}}{A_1} = 90^\circ }$

#4

Al.Koutsouridis έγραψε: ↑
Τρί Ιαν 21, 2020 9:53 pm
Ανοιχτή Ολυμπιάδα Φυσικομαθηματικού Λυκείου 239 Αγίας Πετρούπολης για τις τάξεις 10η και 11η, 2015.

Αλέξανδρε, καλησπέρα και ευχαριστούμε πολύ για τις μεταφράσεις σου!

Εξήγησέ μας , όταν λέμε Λύκειο, τι Λύκειο είναι αυτό. Και τι διαγωνισμός είναι αυτός. Εμείς εδώ, τώρα, τι να κάνουμε, να μελαγχολήσουμε, να κλάψουμε ή να αλλάξουμε επάγγελμα;

#5

ΦΩΤΙΑΔΗΣ ΠΡΟΔΡΟΜΟΣ έγραψε: ↑
Τρί Ιαν 21, 2020 10:36 pm

Al.Koutsouridis έγραψε: ↑
Τρί Ιαν 21, 2020 9:53 pm
Ανοιχτή Ολυμπιάδα Φυσικομαθηματικού Λυκείου 239 Αγίας Πετρούπολης για τις τάξεις 10η και 11η, 2015.

1. Ο εγγεγραμμένος κύκλος του τριγώνου εφάπτεται των πλευρών του στα σημεία $C_{1}, A_{1}, B_{1}$ αντίστοιχα. Η ευθεία $A_{1}C_{1}$ τέμνει την παράλληλη από το σημείο ως προς την πλευρά , στο σημείο . Να αποδείξετε, ότι $\angle KB_{1}A_{1}=90^0$ .

210.PNG

Έστω το έκκεντρο και $L\equiv B_1C_1\cap A_1I$ .Έστω η τομή της με τον έγκυκλο.
Το ανήκει στην πολική του άρα από La Hire το είναι σημείο της πολικής του η οποία θα είναι κάθετη στην άρα παράλληλη στην ,δηλαδή η .Το λοιπόν ανήκει στην πολική του άρα η πολική του θα περνά από το .Όμως ως γνωστών η πολική του θα περνά από το σημείο τομής των , έτσι έχουμε ότι συνευθειακά και το ζητούμενο έπεται.

Καλό!

#6

rek2 έγραψε: ↑
Τετ Ιαν 22, 2020 4:52 pm

Al.Koutsouridis έγραψε: ↑
Τρί Ιαν 21, 2020 9:53 pm
Ανοιχτή Ολυμπιάδα Φυσικομαθηματικού Λυκείου 239 Αγίας Πετρούπολης για τις τάξεις 10η και 11η, 2015.

Αλέξανδρε, καλησπέρα και ευχαριστούμε πολύ για τις μεταφράσεις σου!

Εξήγησέ μας , όταν λέμε Λύκειο, τι Λύκειο είναι αυτό. Και τι διαγωνισμός είναι αυτός. Εμείς εδώ, τώρα, τι να κάνουμε, να μελαγχολήσουμε, να κλάψουμε ή να αλλάξουμε επάγγελμα;

Καλησπέρα!

Το #239 της Α.Πετρούπολης είναι ειδικό σχολείο. Δείτε κι εδώ.

"...
Το Σχολείο της Αγίας Πετρούπολης #239.

Ερευνώντας περισσότερο το θέμα των ειδικών σχολείων μαθηματικών και φυσικής διαπιστώνουμε ότι η περίπτωση του #57 δεν είναι η μοναδική.

Ένα ακόμη σχολείο με προχωρημένο πρόγραμμα μαθηματικών είναι το Σχολείο της Αγίας Πετρούπολης #239. Ανάμεσα στους απόφοιτους του συναντάμε τον Grigori Perelman και τον Stanislav Smirnov, δύο κατόχους του πιο σημαντικού βραβείου στα μαθηματικά, του Fields Medal, αλλά και πολλούς άλλους καθηγητές πανεπιστημίου και εξέχοντες μαθηματικούς, αναγνωρισμένους διεθνώς!

Μαθητές του σχολείου αυτού διακρίνονται κατ' επανάληψη σε απαιτητικούς μαθηματικούς διαγωνισμούς και αποτελούν μέλη της εθνικής ομάδας της Ρωσίας στις Διεθνείς Μαθηματικές Ολυμπιάδες. Το 2013, τρία από τα έξι μέλη ήταν μαθητές του #239.

Από το 2015 έως το 2017, το #239 κατατάχθηκε πρώτο στη λίστα με τα πεντακόσια καλύτερα σχολεία της Ρωσίας, ενώ το 2013 και το 2014 ήταν τρίτο. Οι καθηγητές του έχουν τιμηθεί επανειλημμένα με βραβεία, τόσο για τις γνώσεις τους όσο και για τιςδιδασκαλικές τους ικανότητες. Πολλοί από αυτούς είναι απόφοιτοι του ίδιου σχολείου και είχαν διακριθεί ως μαθητές σε Πανρωσικές ή Διεθνείς μαθηματικές Ολυμπιάδες.
...
"

Φιλικά,

Αχιλλέας

Al.Koutsouridis · #7

rek2 έγραψε: ↑
Τετ Ιαν 22, 2020 4:52 pm

Al.Koutsouridis έγραψε: ↑
Τρί Ιαν 21, 2020 9:53 pm
Ανοιχτή Ολυμπιάδα Φυσικομαθηματικού Λυκείου 239 Αγίας Πετρούπολης για τις τάξεις 10η και 11η, 2015.

Εξήγησέ μας , όταν λέμε Λύκειο, τι Λύκειο είναι αυτό. Και τι διαγωνισμός είναι αυτός. Εμείς εδώ, τώρα, τι να κάνουμε, να μελαγχολήσουμε, να κλάψουμε ή να αλλάξουμε επάγγελμα;

Καλησπέρα κ.Κώστα!

Όσο αναφορά το τι μπορούμε να κάνουμε εμείς δε ξέρω, θα μπορούσαμε όμως να συλλογιστούμε. Όσο αναφορά το σχολείο, όπως ωραία και εύστοχα έγραψε ο κ. Αχιλλέας παραπάνω, το Λύκειο αυτό είναι ένα ειδικό σχολείο που έχει πιο προχωρημένο πρόγραμμα στις θετικές επιστήμες γενικότερα. Η αλήθεια είναι ανά διαστήματα προσπάθησα να βρω το αναλυτικό πρόγραμμα στα μαθηματικά αλλά δεν έχω καταφέρει κάτι ακόμα.

Για τον διαγωνισμό: Ο διαγωνισμός αυτός είναι ανοιχτός με την έννοια ότι μπορεί να συμμετάσχει ο καθένας και θεωρείτε ως συμπλήρωμα στην ολυμπιάδα της Αγίας Πετρούπολης (αναφέρεται ως ολυμπιάδα πόλης), παρότι δεν είναι κομμάτι αυτής. Οι θεματοδότες στην πλειοψηφία τους είναι οι ίδιοι και είναι δάσκαλοι του Λυκείου. Πρακτικά, λόγω των θεμάτων, προσελκύει τους δυνατούς μαθητές των φυσικομαθηματικών σχολείων της Α. Πετρούπολης και είναι προφορική όπως και της πόλης.

Σαν σχολείο έχει ενδιαφέρουσα ιστορία, ίσως μεταφέρω μερικά σημεία αργότερα. Στην σύγχρονη μορφή του συνοπτικά μπορούμε να πούμε τα παρακάτω:

Από το 2014 έχει το μοναδικό στάτους στην Ρωσία ως Προεδρικό φυσικομαθηματικό λύκειο, που στην ουσία του δίνει την δυνατότητα και σε μαθητές άλλων πόλεων να φοιτούν σε αυτό. Από το 2016 λειτουργούν προγράμματα ανοιχτού σχολείο δίνοντας την δυνατότητα σε μαθητές απομακρυσμένων περιοχών να παρακολουθούν το πρόγραμμά του. Για την εισαγωγή τους στο ανοιχτό σχολείο οι μαθητές δίνουν διαδικτυακά εξετάσεις ή μέσο των περιφερειακών προγραμμάτων «Sirius». Η εισαγωγή γενικότερα από ότι έχω καταλάβει γίνεται μέσο διαγωνισμού στην 5η τάξη ("Ανοιχτή ολυμπιάδα για την 5η τάξη").

Την τρέχουσα στιγμή το σχολείο έχει 30 τάξεις (από 5η μέχρι 11η) και 866 μαθητές. Όλες οι τάξεις είναι τάξεις εμβάθυνσης στα μαθηματικά και την φυσική και από το 2019 και τάξεις χημείας-βιολογίας. Λειτουργούν και ξεχωριστοί όμιλοι, κύκλοι 252 τον αριθμό με περισσότερους από 2500 μαθητές σε 85 προγράμματα σε 5 κατευθύνσεις. Πολλοί από τους οποίους δεν είναι μαθητές του σχολείου. Συγκεκριμένα ο μαθηματικός όμιλος-κύκλος είναι ο παλιότερος στην Ρωσία και λειτουργεί από το 1934.

Το σχολείο έχει ειδικά εργαστήρια ρομποτικής, μικροηλεκτρονικής, ηλεκτρολογίας, οπτικής, νάνο-τεχνολογίας, δυο εργαστήρια χημείας, ψηφιακής μουσικής, εκδοτικό οίκο. Παρέχει διαδικτυακά διαλέξεις (lektorium.tv). Καθώς διεξάγει και πολλά καλοκαιρινά σχολεία μαθηματικών, ρομποτικής, φυσικής.

Ορέστης Λιγνός · #8

Al.Koutsouridis έγραψε: ↑
Τρί Ιαν 21, 2020 9:53 pm
Ανοιχτή Ολυμπιάδα Φυσικομαθηματικού Λυκείου 239 Αγίας Πετρούπολης για τις τάξεις 10η και 11η, 2015.

6. Δίνονται οι θετικοί αριθμοί που ικανοποιούν την ισότητα

.

Να αποδείξετε την ανισότητα

$2ab(a-b)^2+2bc(b-c)^2+2ca(c-a)^2 \geq (ab+bc+ca)^2$ .

Από Cauchy-Schwarz, είναι $\displaystyle \sum \dfrac{(2a-b)^2}{c} \geqslant \dfrac{(2a-b+2b-c+2c-a)^2}{a+b+c}=a+b+c$ , οπότε έχουμε $\displaystyle \sum \dfrac{(2a-b)^2}{c} \geqslant a+b+c \Rightarrow 4\sum \dfrac{a^2}{c} +\sum \dfrac{a^2}{b} \geqslant 4\sum \dfrac{ab}{c}+\sum a$ (1).

Επίσης, διαιρώντας και τα 2 μέλη της συνθήκης με abc

, έχουμε $\displaystyle 2\sum \dfrac{a^2}{c}=\sum \dfrac{ab}{c}$ (2)

Διαιρώντας τώρα και τα 2 μέλη της προς απόδειξη με abc

και κάνοντας πράξεις, αρκεί $\displaystyle 2\sum \dfrac{a^2}{c}+2\sum \dfrac{a^2}{b} \geqslant 5\sum \dfrac{ab}{c}+2\sum a$ .

Έστω τώρα, $\displaystyle \sum \dfrac{a^2}{b}=P, \sum \dfrac{a^2}{c}=Q, \sum \dfrac{ab}{c}=R, \sum a= S$ .

Η (1) γράφεται $4Q+P \geqslant 4R+S$ και η (2) 2Q=R

, ενώ αρκεί $2Q+2P \geqslant 5R+2S$ .

Αυτό όμως είναι προφανές, καθώς $2Q+2P=2Q-R+2P+R=2P+R=5R+2S+2(P-2R-S) \geqslant$ 5R+2S +2(4R+S-4Q-2R-S)=5R+2S+2(2R-4Q)=5R+2S

.

Η απόδειξη ολοκληρώθηκε.

qwerty · #9

achilleas έγραψε: ↑
Τετ Ιαν 22, 2020 6:16 pm

rek2 έγραψε: ↑
Τετ Ιαν 22, 2020 4:52 pm

Al.Koutsouridis έγραψε: ↑
Τρί Ιαν 21, 2020 9:53 pm
Ανοιχτή Ολυμπιάδα Φυσικομαθηματικού Λυκείου 239 Αγίας Πετρούπολης για τις τάξεις 10η και 11η, 2015.

Αλέξανδρε, καλησπέρα και ευχαριστούμε πολύ για τις μεταφράσεις σου!

Εξήγησέ μας , όταν λέμε Λύκειο, τι Λύκειο είναι αυτό. Και τι διαγωνισμός είναι αυτός. Εμείς εδώ, τώρα, τι να κάνουμε, να μελαγχολήσουμε, να κλάψουμε ή να αλλάξουμε επάγγελμα;

Καλησπέρα!

Το #239 της Α.Πετρούπολης είναι ειδικό σχολείο. Δείτε κι εδώ.

"...
Το Σχολείο της Αγίας Πετρούπολης #239.

Ερευνώντας περισσότερο το θέμα των ειδικών σχολείων μαθηματικών και φυσικής διαπιστώνουμε ότι η περίπτωση του #57 δεν είναι η μοναδική.

Ένα ακόμη σχολείο με προχωρημένο πρόγραμμα μαθηματικών είναι το Σχολείο της Αγίας Πετρούπολης #239. Ανάμεσα στους απόφοιτους του συναντάμε τον Grigori Perelman και τον Stanislav Smirnov, δύο κατόχους του πιο σημαντικού βραβείου στα μαθηματικά, του Fields Medal, αλλά και πολλούς άλλους καθηγητές πανεπιστημίου και εξέχοντες μαθηματικούς, αναγνωρισμένους διεθνώς!

Μαθητές του σχολείου αυτού διακρίνονται κατ' επανάληψη σε απαιτητικούς μαθηματικούς διαγωνισμούς και αποτελούν μέλη της εθνικής ομάδας της Ρωσίας στις Διεθνείς Μαθηματικές Ολυμπιάδες. Το 2013, τρία από τα έξι μέλη ήταν μαθητές του #239.

Από το 2015 έως το 2017, το #239 κατατάχθηκε πρώτο στη λίστα με τα πεντακόσια καλύτερα σχολεία της Ρωσίας, ενώ το 2013 και το 2014 ήταν τρίτο. Οι καθηγητές του έχουν τιμηθεί επανειλημμένα με βραβεία, τόσο για τις γνώσεις τους όσο και για τιςδιδασκαλικές τους ικανότητες. Πολλοί από αυτούς είναι απόφοιτοι του ίδιου σχολείου και είχαν διακριθεί ως μαθητές σε Πανρωσικές ή Διεθνείς μαθηματικές Ολυμπιάδες.
...
"

Φιλικά,

Αχιλλέας

Έχω ακούσει (δεν το πρόλαβα εγώ) οτι και στην Ελλάδα υπήρχαν ειδικά σχολεία για θετικές επιστήμες, τα πρακτικά λύκεια. Αυτά ήταν κάτι αντίστοιχο με το προαναφερθέν ρωσικό σχολείο;

#10

qwerty έγραψε: ↑
Σάβ Ιαν 25, 2020 10:15 pm
Έχω ακούσει (δεν το πρόλαβα εγώ) οτι και στην Ελλάδα υπήρχαν ειδικά σχολεία για θετικές επιστήμες, τα πρακτικά λύκεια. Αυτά ήταν κάτι αντίστοιχο με το προαναφερθέν ρωσικό σχολείο;

Αχιλλέα, δεν αληθεύει αυτό.

Αυτό που ίσχυε είναι ότι οι δύο τελευταίες τάξεις του Σχολείου χωριζόντουσαν σε δύο κλάδους.
Ο ένας ονομαζόταν "Κλασικό" και απευθυνόταν σε αυτούς που ενδιαφερόντουσαν για φιλολογικές, ιστορικές και λοιπά
σπουδές. Π.χ. μάθαιναν Αρχαία Ελληνικά, Λατινικά κλπ, αλλά έκαναν και Μαθηματικά.
Ο άλλος κλάδος ήταν το "Πρακτικό". Απευθυνόταν σε αυτούς που ενδιαφερόντουσαν για Φυσικομαθηματικές και Πολυτεχνικές
σπουδές. Έκαναν περισσότερα Μαθηματικά από τους άλλους, αλλά έκαναν και Αρχαία Ελληνικά (όχι όμως Λατινικά).

Με άλλα λόγια, δεν υπήρχαν ειδικά Σχολεία για Πρακτικό αλλά όλα τα Σχολεία ήταν Κλασικό-Πρακτικό (εκτός από μερικά στην
επαρχία, που δεν είχαν την πολυτέλεια να έχουν δύο τομείς).

#11

Mihalis_Lambrou έγραψε: ↑
Σάβ Ιαν 25, 2020 11:12 pm

qwerty έγραψε: ↑
Σάβ Ιαν 25, 2020 10:15 pm
Έχω ακούσει (δεν το πρόλαβα εγώ) οτι και στην Ελλάδα υπήρχαν ειδικά σχολεία για θετικές επιστήμες, τα πρακτικά λύκεια. Αυτά ήταν κάτι αντίστοιχο με το προαναφερθέν ρωσικό σχολείο;
Αχιλλέα, δεν αληθεύει αυτό.

...

Δεν είπα ότι αληθεύει.

qwerty · #12

Εγώ το πα. Ευχαριστώ τον Μιχάλη Λάμπρου για τις πληροφορίες.

Ανδρέας Πούλος · #13

Με αφορμή τη συζήτηση για τα σχολεία επιστημών, στο πλαίσιο του Εθνικού Διαλόγου για την Παιδεία το 2016 είχα υποβάλλει μία σχετική επίσημη πρόταση στο Υπουργείο Παιδείας.
Ποτέ δεν έλαβα κάποια απάντηση, ούτε ότι παρέλαβαν την πρόταση.
Επειδή το αρχείο είναι "μεγάλο" για τον χώρο του Φόρουμ, αναρτώ μία περίληψή του που υπέβαλα στο Συνέδριο της ΕΝΕ.ΠΡΟΤ.

Ιδρυση σχολείων Επιστημών για ΕΝ.Ε.ΠΡΟΤ..pdf: (531.62 KiB) Μεταφορτώθηκε 23 φορές

Την αναρτώ εδώ δημόσια.

Ανοιχτή Ολυμπιάδα ΦΜΛ 239 (10-11η τάξη, 2015)

Ανοιχτή Ολυμπιάδα ΦΜΛ 239 (10-11η τάξη, 2015)

Re: Ανοιχτή Ολυμπιάδα ΦΜΛ 239 (10-11η τάξη, 2015)

Re: Ανοιχτή Ολυμπιάδα ΦΜΛ 239 (10-11η τάξη, 2015)

Re: Ανοιχτή Ολυμπιάδα ΦΜΛ 239 (10-11η τάξη, 2015)

Re: Ανοιχτή Ολυμπιάδα ΦΜΛ 239 (10-11η τάξη, 2015)

Re: Ανοιχτή Ολυμπιάδα ΦΜΛ 239 (10-11η τάξη, 2015)

Re: Ανοιχτή Ολυμπιάδα ΦΜΛ 239 (10-11η τάξη, 2015)

Re: Ανοιχτή Ολυμπιάδα ΦΜΛ 239 (10-11η τάξη, 2015)

Re: Ανοιχτή Ολυμπιάδα ΦΜΛ 239 (10-11η τάξη, 2015)

Re: Ανοιχτή Ολυμπιάδα ΦΜΛ 239 (10-11η τάξη, 2015)

Re: Ανοιχτή Ολυμπιάδα ΦΜΛ 239 (10-11η τάξη, 2015)

Re: Ανοιχτή Ολυμπιάδα ΦΜΛ 239 (10-11η τάξη, 2015)

Re: Ανοιχτή Ολυμπιάδα ΦΜΛ 239 (10-11η τάξη, 2015)

Μέλη σε σύνδεση