υ.γ: Όποιος μπορέσει ας ανεβάσει τα θέματα!!
IMO 2019
Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
-
Τσιαλας Νικολαος
- Δημοσιεύσεις: 789
- Εγγραφή: Σάβ Ιαν 17, 2015 1:04 pm
IMO 2019
Αύριο ξεκινάει η IMO 2019 στο Bath της Αγγλίας. Εύχομαι καλή επιτυχία στην Ελληνική και την Κυπριακή αποστολή αλλά και στους συνοδούς silouan και demetres!! 




υ.γ: Όποιος μπορέσει ας ανεβάσει τα θέματα!!
υ.γ: Όποιος μπορέσει ας ανεβάσει τα θέματα!!
Λέξεις Κλειδιά:
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13277
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
- S.E.Louridas
- Δημοσιεύσεις: 5956
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
Re: IMO 2019
Να ευχηθώ από καρδιάς στους Έλληνες Διαγωνιζόμενους, αλλά και στούς Κύπριους αδελφούς μας διαγωνιζόμενους, Καλή Επιτυχία και Καλή Επάνοδο.
Δηλώνουμε υπερήφανοι για σας, αφού αποτελείτε ηχηρότατη απάντηση στην πρόκληση της εποχής.
Δηλώνουμε υπερήφανοι για σας, αφού αποτελείτε ηχηρότατη απάντηση στην πρόκληση της εποχής.
S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
Re: IMO 2019
Το πρώτο πρόβλημα είναι.
Αν
είναι το σύνολο των ακεραίων
να βρείτε όλες τις συναρτήσεις

για τις οποίες ισχύει ,
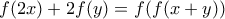
για όλα τα
Αν

είναι το σύνολο των ακεραίων
να βρείτε όλες τις συναρτήσεις

για τις οποίες ισχύει ,
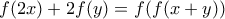
για όλα τα

-
jason.prod
- Δημοσιεύσεις: 141
- Εγγραφή: Τρί Φεβ 25, 2014 5:29 pm
Re: IMO 2019
Νομίζω αρκετά εύκολη για ΙΜΟ.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τρί Ιούλ 16, 2019 3:56 pmΤο πρώτο πρόβλημα είναι.
Αν
είναι το σύνολο των ακεραίων
να βρείτε όλες τις συναρτήσεις
για τις οποίες ισχύει ,
για όλα τα
Απλώς βάλτε
 και μετά
και μετά 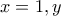 το
το  και έχει βγει γραμμική. Τα άλλα θέμα ρουτίνας.
και έχει βγει γραμμική. Τα άλλα θέμα ρουτίνας.Προδρομίδης Κυπριανός-Ιάσων
-
Τσιαλας Νικολαος
- Δημοσιεύσεις: 789
- Εγγραφή: Σάβ Ιαν 17, 2015 1:04 pm
Re: IMO 2019
Για  λαμβάνουμε
λαμβάνουμε 
και για παίρνουμε
παίρνουμε  .
.
Τότε από την προκύπτει
προκύπτει 
Από τις σχέσεις η αρχική γίνεται
η αρχική γίνεται

Έστω .
.
Αντικαθιστώντας στην προκύπτει ότι
προκύπτει ότι 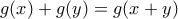 ,
,
δηλαδή η ικανοποιεί την συναρτησιακή εξίσωση του Cauchy, άρα
ικανοποιεί την συναρτησιακή εξίσωση του Cauchy, άρα

Αντικαθιστώντας στην αρχική λαμβάνουμε τις λύσεις:
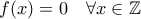

EDIT: Καλή επιτυχία στις ομάδες της Ελλάδας και της Κύπρου!
 λαμβάνουμε
λαμβάνουμε 
και για
 παίρνουμε
παίρνουμε  .
.Τότε από την
 προκύπτει
προκύπτει 
Από τις σχέσεις
 η αρχική γίνεται
η αρχική γίνεται 
Έστω
 .
.Αντικαθιστώντας στην
 προκύπτει ότι
προκύπτει ότι 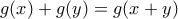 ,
,δηλαδή η
 ικανοποιεί την συναρτησιακή εξίσωση του Cauchy, άρα
ικανοποιεί την συναρτησιακή εξίσωση του Cauchy, άρα 
Αντικαθιστώντας στην αρχική λαμβάνουμε τις λύσεις:
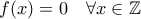

EDIT: Καλή επιτυχία στις ομάδες της Ελλάδας και της Κύπρου!
Re: IMO 2019
ΓιαΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τρί Ιούλ 16, 2019 3:56 pmΤο πρώτο πρόβλημα είναι.
Αν
είναι το σύνολο των ακεραίων
να βρείτε όλες τις συναρτήσεις
για τις οποίες ισχύει ,
για όλα τα
 έχουμε
έχουμε 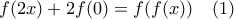 ,
, ενώ για
 έχουμε
έχουμε  .
. Για
 οι 2 τελευταίες δινουν
οι 2 τελευταίες δινουν  .
. Η αρχική μαζί με τη (2) δίνουν:
 .
. Η τελευταία, χρησιμοποιώντας και την (3), γίνεται
 , η οποία για
, η οποία για  δίνει
δίνει  για κάθε
για κάθε  , με
, με  . Λύνοντας την αναδρομική έχουμε
. Λύνοντας την αναδρομική έχουμε  για
για  και
και  σταθερά. Με αντικατάσταση στην αρχική και εξίσωση συντελεστών βγάζουμε οτι πρέπει και αρκεί
σταθερά. Με αντικατάσταση στην αρχική και εξίσωση συντελεστών βγάζουμε οτι πρέπει και αρκεί 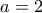 ή
ή  , άρα οι λύσεις είναι ολες οι
, άρα οι λύσεις είναι ολες οι 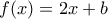 για
για  ακέραιο και η μηδενική.
ακέραιο και η μηδενική.Κολλιοπουλος Νικος.
Μεταδιδακτορικός ερευνητής.
Ερευνητικά ενδιαφέροντα: Στοχαστικές ΜΔΕ, ασυμπτωτική ανάλυση στοχαστικών συστημάτων, εφαρμογές αυτών στα χρηματοοικονομικά και στη διαχείριση ρίσκων.
Μεταδιδακτορικός ερευνητής.
Ερευνητικά ενδιαφέροντα: Στοχαστικές ΜΔΕ, ασυμπτωτική ανάλυση στοχαστικών συστημάτων, εφαρμογές αυτών στα χρηματοοικονομικά και στη διαχείριση ρίσκων.
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13277
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: IMO 2019
Το  o πρόβλημα (Γεωμετρία)
Σε τρίγωνο
o πρόβλημα (Γεωμετρία)
Σε τρίγωνο  , το
, το  είναι σημείο της πλευράς
είναι σημείο της πλευράς  και το
και το  σημείο της πλευράς
σημείο της πλευράς  . Έστω
. Έστω  και
και  σημεία των τμημάτων
σημεία των τμημάτων
 και
και  , αντίστοιχα, έτσι ώστε το
, αντίστοιχα, έτσι ώστε το  να είναι παράλληλο στο
να είναι παράλληλο στο  . Έστω
. Έστω 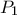 σημείο της ευθείας
σημείο της ευθείας 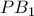 , ώστε το
, ώστε το  να
να
είναι ανάμεσα στα και
και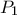 , και
, και 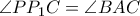 . Ομοίως, έστω
. Ομοίως, έστω  σημείο της ευθείας
σημείο της ευθείας  , ώστε το
, ώστε το  να είναι ανάμεσα
να είναι ανάμεσα
στα και
και  , και
, και  . Να δείξετε ότι τα σημεία
. Να δείξετε ότι τα σημεία 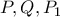 , και
, και  είναι ομοκυκλικά..
είναι ομοκυκλικά..
 o πρόβλημα (Γεωμετρία)
Σε τρίγωνο
o πρόβλημα (Γεωμετρία)
Σε τρίγωνο  , το
, το  είναι σημείο της πλευράς
είναι σημείο της πλευράς  και το
και το  σημείο της πλευράς
σημείο της πλευράς  . Έστω
. Έστω  και
και  σημεία των τμημάτων
σημεία των τμημάτων  και
και  , αντίστοιχα, έτσι ώστε το
, αντίστοιχα, έτσι ώστε το  να είναι παράλληλο στο
να είναι παράλληλο στο  . Έστω
. Έστω 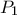 σημείο της ευθείας
σημείο της ευθείας 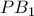 , ώστε το
, ώστε το  να
να είναι ανάμεσα στα
 και
και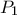 , και
, και 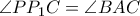 . Ομοίως, έστω
. Ομοίως, έστω  σημείο της ευθείας
σημείο της ευθείας  , ώστε το
, ώστε το  να είναι ανάμεσα
να είναι ανάμεσα στα
 και
και  , και
, και  . Να δείξετε ότι τα σημεία
. Να δείξετε ότι τα σημεία 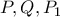 , και
, και  είναι ομοκυκλικά..
είναι ομοκυκλικά..- polysot
- Επιμελητής
- Δημοσιεύσεις: 2583
- Εγγραφή: Δευ Οκτ 19, 2009 11:43 pm
- Τοποθεσία: Όπου βρω ενδιαφέρουσες προσωπικότητες...
- Επικοινωνία:
Re: IMO 2019
Πρόβλημα 3
Ένα κοινωνικό δίκτυο έχει 2019 χρήστες και κάποια ζεύγη εξ αυτών είναι φίλοι. ΑΝ ένας χρήστης Α είναι φίλος με ένα χρήστη Β, τότε και ο Β είναι φίλος με τον Α. Μπορούν να συμβαίνουν επαναλαμβανόμενα ένα και μόνο ένα γεγονός όπως το παρακάτω κάθε φορά:
Τρεις χρήστες τέτοιοι, ώστε ο
τέτοιοι, ώστε ο  είναι φίλος και με τους δύο
είναι φίλος και με τους δύο  , αλλά οι
, αλλά οι 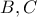 δεν είναι φιλοι μεταξύ τους, αλλάζουν τις καταστάσεις φιλίας τους έτσι ώστε οι
δεν είναι φιλοι μεταξύ τους, αλλάζουν τις καταστάσεις φιλίας τους έτσι ώστε οι  είναι τώρα φίλοι, αλλά ο
είναι τώρα φίλοι, αλλά ο  δεν είναι πλέον φίλος με τον
δεν είναι πλέον φίλος με τον  , ούτε με τον
, ούτε με τον  . Όλες οι υπολοιπες φιλίες παραμένουν ίδιες.
. Όλες οι υπολοιπες φιλίες παραμένουν ίδιες.
ΑΡχικά, χρήστες έχουν
χρήστες έχουν  φίλους ο καθένας και
φίλους ο καθένας και  χρήστες έχουν
χρήστες έχουν  φίλους ο καθένας. Αποδείξετε ότι υπάρχει ακολουθία τέτοιων γεγονότων μετά από την οποία κάθε χρήστης είναι φίλος με έναν το πολύ άλλον χρήστη.
φίλους ο καθένας. Αποδείξετε ότι υπάρχει ακολουθία τέτοιων γεγονότων μετά από την οποία κάθε χρήστης είναι φίλος με έναν το πολύ άλλον χρήστη.
Ένα κοινωνικό δίκτυο έχει 2019 χρήστες και κάποια ζεύγη εξ αυτών είναι φίλοι. ΑΝ ένας χρήστης Α είναι φίλος με ένα χρήστη Β, τότε και ο Β είναι φίλος με τον Α. Μπορούν να συμβαίνουν επαναλαμβανόμενα ένα και μόνο ένα γεγονός όπως το παρακάτω κάθε φορά:
Τρεις χρήστες
 τέτοιοι, ώστε ο
τέτοιοι, ώστε ο  είναι φίλος και με τους δύο
είναι φίλος και με τους δύο  , αλλά οι
, αλλά οι 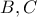 δεν είναι φιλοι μεταξύ τους, αλλάζουν τις καταστάσεις φιλίας τους έτσι ώστε οι
δεν είναι φιλοι μεταξύ τους, αλλάζουν τις καταστάσεις φιλίας τους έτσι ώστε οι  είναι τώρα φίλοι, αλλά ο
είναι τώρα φίλοι, αλλά ο  δεν είναι πλέον φίλος με τον
δεν είναι πλέον φίλος με τον  , ούτε με τον
, ούτε με τον  . Όλες οι υπολοιπες φιλίες παραμένουν ίδιες.
. Όλες οι υπολοιπες φιλίες παραμένουν ίδιες.ΑΡχικά,
 χρήστες έχουν
χρήστες έχουν  φίλους ο καθένας και
φίλους ο καθένας και  χρήστες έχουν
χρήστες έχουν  φίλους ο καθένας. Αποδείξετε ότι υπάρχει ακολουθία τέτοιων γεγονότων μετά από την οποία κάθε χρήστης είναι φίλος με έναν το πολύ άλλον χρήστη.
φίλους ο καθένας. Αποδείξετε ότι υπάρχει ακολουθία τέτοιων γεγονότων μετά από την οποία κάθε χρήστης είναι φίλος με έναν το πολύ άλλον χρήστη.Σωτήρης Δ. Χασάπης
Ζήσε τα μαθηματικά σου!
-----------------------------
"There is a scientific taste just as there is a literary or artistic one", Renan
"The journey of a thousand miles begins with one step.", Lao Tzu
Ζήσε τα μαθηματικά σου!
-----------------------------
"There is a scientific taste just as there is a literary or artistic one", Renan
"The journey of a thousand miles begins with one step.", Lao Tzu
- S.E.Louridas
- Δημοσιεύσεις: 5956
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
Re: IMO 2019
Επί του πιεστηρίου μία άποψη για το δεύτερο της γεωμετρίας:
.........................
O τρόπος που "έστησα" την άποψη μου (δυστυχώς λόγω βιασύνης) ήταν κακός, οπότε τον αποσύρω με όλες τις ειλικρινείς συγγνώμες.
.........................
O τρόπος που "έστησα" την άποψη μου (δυστυχώς λόγω βιασύνης) ήταν κακός, οπότε τον αποσύρω με όλες τις ειλικρινείς συγγνώμες.
τελευταία επεξεργασία από S.E.Louridas σε Παρ Ιούλ 19, 2019 1:27 pm, έχει επεξεργασθεί 2 φορές συνολικά.
S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
-
AlexNtagkas
- Δημοσιεύσεις: 9
- Εγγραφή: Κυρ Ιαν 20, 2019 8:46 am
Re: IMO 2019
Μια απλη και ευκολη ( αλλα αρκετα εκτενης ) λυση στη γεωμετρια προκυπτει Αν θεωρησουμε 
και
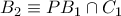
οπου ο περιγεγραμμενος του ABC.
ο περιγεγραμμενος του ABC.
Τοτε βγαινουν εγγραψιμα τα :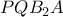


οποτε μετα απο "angle chasing" Βγαινουν και τα

Και τελικα βγαινει το ζητουμενο

και
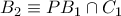
οπου
 ο περιγεγραμμενος του ABC.
ο περιγεγραμμενος του ABC.Τοτε βγαινουν εγγραψιμα τα :
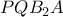


οποτε μετα απο "angle chasing" Βγαινουν και τα


Και τελικα βγαινει το ζητουμενο
τελευταία επεξεργασία από AlexNtagkas σε Τετ Ιούλ 17, 2019 8:16 pm, έχει επεξεργασθεί 1 φορά συνολικά.
-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5561
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
- S.E.Louridas
- Δημοσιεύσεις: 5956
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
Re: IMO 2019
Καλά αποτελέσματα και καλή επάνοδο σε όλους τους διαγωνιζόμενους της Ελλάδας και της Κύπρου.
S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
Re: IMO 2019
Θα μπορούσατε να γράψετε τις λεπτομέρειες της λύσης αυτής;S.E.Louridas έγραψε: ↑Τετ Ιούλ 17, 2019 3:00 pmΕπί του πιεστηρίου μία άποψη για το δεύτερο της γεωμετρίας:
Αν ητμήσει τις
στα σημεία
αντίστοιχα, τότε οι περιγεγραμμένοι κύκλοι στα τρίγωνα
που εφάπτονται στο
και στα τρίγωνα
και
, οδηγούν στην λύση.
Σιλουανός Μπραζιτίκος
-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
-
christinat
- Δημοσιεύσεις: 50
- Εγγραφή: Κυρ Δεκ 23, 2018 11:26 pm
- Τοποθεσία: Αθήνα
Re: IMO 2019
Αν  από την συναρτησιακη είναι:
από την συναρτησιακη είναι:  (1)
(1)
Αν τοτε
τοτε  (2)
(2)
Αν
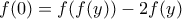
Με αλλαγή μεταβλητής η παραπάνω σχεση γίνεται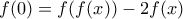 (3)
(3)
Θέτοντας στην σχεση (3) όπου προκύπτει ότι
προκύπτει ότι 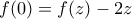
Οποτε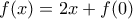 ,για κάθε ακέραιο
,για κάθε ακέραιο 
Από τις σχέσεις (2)-(3):
 (4)
(4)
Από τις σχέσεις (3)-(4):

Αφου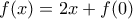 τοτε
τοτε 

Προσθέτοντας τις δυο τελευταίες σχέσεις κατά μέλη:
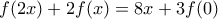
Οποτε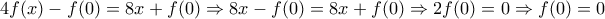
Αν τοτε από την (3) είναι
τοτε από την (3) είναι 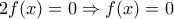 για κάθε ακέραιο
για κάθε ακέραιο 
Άρα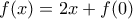 ή
ή 
 από την συναρτησιακη είναι:
από την συναρτησιακη είναι:  (1)
(1)Αν
 τοτε
τοτε  (2)
(2)Αν

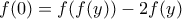
Με αλλαγή μεταβλητής η παραπάνω σχεση γίνεται
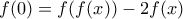 (3)
(3)Θέτοντας στην σχεση (3) όπου
 προκύπτει ότι
προκύπτει ότι 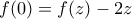
Οποτε
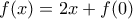 ,για κάθε ακέραιο
,για κάθε ακέραιο 
Από τις σχέσεις (2)-(3):
 (4)
(4)Από τις σχέσεις (3)-(4):

Αφου
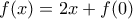 τοτε
τοτε 

Προσθέτοντας τις δυο τελευταίες σχέσεις κατά μέλη:
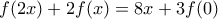
Οποτε
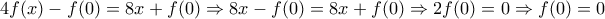
Αν
 τοτε από την (3) είναι
τοτε από την (3) είναι 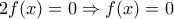 για κάθε ακέραιο
για κάθε ακέραιο 
Άρα
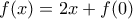 ή
ή 
τελευταία επεξεργασία από christinat σε Παρ Δεκ 18, 2020 7:06 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Re: IMO 2019
Χριστίνα καλησπέρα, το παραπάνω έχει λάθος, δεν δικαιούσαι να πεις ότι:christinat έγραψε: ↑Πέμ Ιούλ 18, 2019 3:38 pm
Με αλλαγή μεταβλητής η παραπάνω σχεση γίνεται(3)
Θέτοντας στην σχεση (3) όπουπροκύπτει ότι
Οποτε,για κάθε ακέραιο
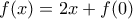 . Ο λόγος είναι ότι το
. Ο λόγος είναι ότι το  που έχεις θεωρήσει είναι εξαρτημένη μεταβλητή, ( αφού είναι ίσο με
που έχεις θεωρήσει είναι εξαρτημένη μεταβλητή, ( αφού είναι ίσο με  ) ενώ το χ στην σχέση
) ενώ το χ στην σχέση 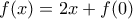 ,για κάθε ακέραιο
,για κάθε ακέραιο  , που καταλήγεις είναι προφανώς, ανεξάρτητη.
, που καταλήγεις είναι προφανώς, ανεξάρτητη.Θα μπορούσες να το πεις αυτό αν η
 ήταν επί των ακεραίων, όμως για παράδειγμα η
ήταν επί των ακεραίων, όμως για παράδειγμα η  που ικανοποιεί την συναρτησιακή δεν είναι επί.Με λίγα λόγια το πρόβλημα είναι το για κάθε ακέραιο
που ικανοποιεί την συναρτησιακή δεν είναι επί.Με λίγα λόγια το πρόβλημα είναι το για κάθε ακέραιο  , καθώς ισχύει μόνο για κάθε ακέραιο στην εικόνα της
, καθώς ισχύει μόνο για κάθε ακέραιο στην εικόνα της  .
.Υ.Γ. Καλή επιτυχία στα παιδιά!
Αρμενιάκος Σωτήρης
- S.E.Louridas
- Δημοσιεύσεις: 5956
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
Re: IMO 2019
Καταρχάς Σιλουανέ, συγγνώμη που άργησα για την απάντηση, αλλά στην δουλειά μου και λόγω ενός διαγωνισμού που θα γίνει για την τράπεζα Ελλάδος εργαζόμαστε πάρα πολλές ώρες και όχι μόνο κάνοντας προσωπικά μάθημα. Έτσι επιφυλάσσομαι και για κάποιες παραλήψεις, επειδή η λύση έγινε βιαστικά, αφού να φανταστείς μόλις πριν μία ώρα γύρισα σπίτι.silouan έγραψε: ↑Τετ Ιούλ 17, 2019 8:44 pmΘα μπορούσατε να γράψετε τις λεπτομέρειες της λύσης αυτής;S.E.Louridas έγραψε: ↑Τετ Ιούλ 17, 2019 3:00 pmΕπί του πιεστηρίου μία άποψη για το δεύτερο της γεωμετρίας:
Αν ητμήσει τις
στα σημεία
αντίστοιχα, τότε οι περιγεγραμμένοι κύκλοι στα τρίγωνα
που εφάπτονται στο
και στα τρίγωνα
και
, οδηγούν στην λύση.
.........................
Τελικά ο τρόπος που "έστησα" την άποψη μου (δυστυχώς λόγω βιασύνης) ήταν κακός, οπότε τον αποσύρω με όλες τις ειλικρινείς συγγνώμες και ειδικά προς τον Σιλουανό που σίγουρα αυτές τις ώρες δίνει σκληρή μάχη για την κατoχύρωση της αξίας των διαγωνιζόμενων στην ΙΜΟ (το έχω ζήσει προσωπικά στο παρελθόν).
S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
Re: IMO 2019
Θερμά Συγχαρητήρια σε όλη την αποστολή στην ΙΜΟ2019!
Δημητρης Μελας (Αργυρό),
Σπύρος Γαλανόπουλος (Χάλκινο),
Ευθύμης Ντόκας (Χάλκινο),
Δημήτρης Λώλας (Εύφημος μνεία),
Μηνάς Μαργαρίτης (Εύφημος μνεία),
Ειρήνη Μηλιώρη (Εύφημος μνεία)
Η επίλυση και μόνο ενός από τα έξι απαιτητικά προβλήματα που τέθηκαν έχει τεράστια αξία. Σας ευχόμαστε ακόμη μεγαλύτερες επιτυχίες στο μέλλον.
Θερμά συγχαρητήρια ακόμη μια φορά τόσο σε εσάς όσο και στον κ. Φελλούρη και τον Σιλουανό.
Φιλικά,
Αχιλλέας
Δημητρης Μελας (Αργυρό),
Σπύρος Γαλανόπουλος (Χάλκινο),
Ευθύμης Ντόκας (Χάλκινο),
Δημήτρης Λώλας (Εύφημος μνεία),
Μηνάς Μαργαρίτης (Εύφημος μνεία),
Ειρήνη Μηλιώρη (Εύφημος μνεία)
Η επίλυση και μόνο ενός από τα έξι απαιτητικά προβλήματα που τέθηκαν έχει τεράστια αξία. Σας ευχόμαστε ακόμη μεγαλύτερες επιτυχίες στο μέλλον.
Θερμά συγχαρητήρια ακόμη μια φορά τόσο σε εσάς όσο και στον κ. Φελλούρη και τον Σιλουανό.
Φιλικά,
Αχιλλέας
- Συνημμένα
-
- imo2019_hel.png (107.87 KiB) Προβλήθηκε 5735 φορές
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 10 επισκέπτες
