 και έστω
και έστω  το μέσο της πλευράς
το μέσο της πλευράς  . Έστω
. Έστω  και
και  τα παράκεντρα των τριγώνων
τα παράκεντρα των τριγώνων 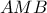 και
και  αντίστοιχα ως προς το σημείο
αντίστοιχα ως προς το σημείο  . Ο περιγεγραμμένος κύκλος του τριγώνου
. Ο περιγεγραμμένος κύκλος του τριγώνου  τέμνει την ευθεία
τέμνει την ευθεία  στα σημεία
στα σημεία  και
και  . Ο περιγεγραμμένος κύκλος του τριγώνου
. Ο περιγεγραμμένος κύκλος του τριγώνου  τέμνει την ευθεία
τέμνει την ευθεία  στα σημεία
στα σημεία  και
και  . Να δειχθεί ότι
. Να δειχθεί ότι  .
. G2. Έστω τρίγωνο
 εγγεγραμμένο σε κύκλο
εγγεγραμμένο σε κύκλο  με κέντρο
με κέντρο  . Έστω
. Έστω  το ορθόκεντρο του
το ορθόκεντρο του  και
και  το μέσο της
το μέσο της 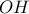 . Η εφαπτομένη του
. Η εφαπτομένη του  στο
στο  τέμνει τη μεσοκάθετο της
τέμνει τη μεσοκάθετο της  στο
στο  και η εφαπτομένη του
και η εφαπτομένη του  στο
στο  τέμνει τη μεσοκάθετο της
τέμνει τη μεσοκάθετο της  στο
στο  . Να δειχθεί ότι οι
. Να δειχθεί ότι οι  και
και 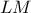 τέμνονται κάθετα.
τέμνονται κάθετα.G3. Έστω
 σημείο μέσα σε τρίγωνο
σημείο μέσα σε τρίγωνο  . Έστω
. Έστω  τα μήκη των πλευρών του
τα μήκη των πλευρών του  και έστω
και έστω  η ημιπερίμετρός του. Να βρεθεί η μέγιστη δυνατή τιμή του
η ημιπερίμετρός του. Να βρεθεί η μέγιστη δυνατή τιμή του 
λαμβάνοντας υπόψη όλες τις διαφορετικές επιλογές τριγώνου
 και σημείου
και σημείου  .
.G4. Αυτό ήταν το πρόβλημα 1 της Βαλκανιάδας.
G5. Έστω οξυγώνιο τρίγωνο
 με
με  και έστω
και έστω  σημείο στην προέκταση του
σημείο στην προέκταση του  από τη μεριά του
από τη μεριά του  . Ο κύκλος
. Ο κύκλος 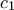 με κέντρο το
με κέντρο το  και ακτίνα
και ακτίνα  τέμνει τις ευθείας
τέμνει τις ευθείας  και
και  στα
στα  και
και  αντίστοιχα. Ο περιγεγραμμένος κύκλος
αντίστοιχα. Ο περιγεγραμμένος κύκλος  του τριγώνου
του τριγώνου 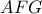 τέμνει ξανά τις ευθείας
τέμνει ξανά τις ευθείας  και
και  στα σημεία
στα σημεία  και
και 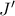 αντίστοιχα. Ο περιγεγραμμένος κύκλος
αντίστοιχα. Ο περιγεγραμμένος κύκλος  του τριγώνου
του τριγώνου 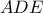 τέμνει ξανά τις ευθείας
τέμνει ξανά τις ευθείας  και
και  στα σημεία
στα σημεία  και
και  αντίστοιχα. Να δειχθεί ότι τα τετράπλευρα
αντίστοιχα. Να δειχθεί ότι τα τετράπλευρα  και
και  είναι κυκλικά με τα κέντρα των περιγεγραμμένων κύκλων τους να συμπίπτουν.
είναι κυκλικά με τα κέντρα των περιγεγραμμένων κύκλων τους να συμπίπτουν.G6. Έστω τρίγωνο
 με
με  με περιγεγραμμένο κύκλο
με περιγεγραμμένο κύκλο  και περίκεντρο
και περίκεντρο  . Έστω
. Έστω  σημείο στην προέκταση της
σημείο στην προέκταση της  από την πλευρά του
από την πλευρά του  . Ο περιγεγραμμένος κύκλος
. Ο περιγεγραμμένος κύκλος  του τριγώνου
του τριγώνου  τέμνει την ευθεία
τέμνει την ευθεία  και τον κύκλο
και τον κύκλο  στα σημεία
στα σημεία  και
και  αντίστοιχα. Το σημείο
αντίστοιχα. Το σημείο  είναι τέτοιο ώστε το τετράπλευρο
είναι τέτοιο ώστε το τετράπλευρο  να είναι παραλληλόγραμμό. Η ευθεία
να είναι παραλληλόγραμμό. Η ευθεία  τέμνει τον κύκλο
τέμνει τον κύκλο  ξανά στο σημείο
ξανά στο σημείο  . Η κάθετη από το
. Η κάθετη από το  στη
στη  τέμνει τον
τέμνει τον  ξανά στο
ξανά στο  και η κάθετη από το
και η κάθετη από το  στη
στη  τέμνει τον
τέμνει τον  ξανά στο
ξανά στο  . Να δειχθεί ότι τα
. Να δειχθεί ότι τα  είναι ομοκυκλικά.
είναι ομοκυκλικά.
 Αρκεί να δείξουμε πως το
Αρκεί να δείξουμε πως το  . Oνομάζουμε
. Oνομάζουμε  τους κύκλους με το σημεία
τους κύκλους με το σημεία  .
. 
 Άρα
Άρα  Oμοίως και από την άλλη πλευρά και καταλήγουμε στο
Oμοίως και από την άλλη πλευρά και καταλήγουμε στο  Όμως
Όμως  άρα
άρα 
 το έγκεντρο και
το έγκεντρο και  οι προβολές του
οι προβολές του 
 με λόγους
με λόγους  αντίστοιχα τέμνονται σε σημείο
αντίστοιχα τέμνονται σε σημείο  εντός του
εντός του 


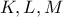 οι προβολές του
οι προβολές του  , έστω στο πρώτο.
, έστω στο πρώτο. και άρα
και άρα  .
. , μια από τις γωνίες είναι μεγαλύτερη ή ίση με
, μια από τις γωνίες είναι μεγαλύτερη ή ίση με  , έστω η
, έστω η  .
. .
. .
. .
. και πιάνεται για
και πιάνεται για  ) του
) του  που είναι και συνηθισμένη τα πράγματα γίνονται πιο απλά.
που είναι και συνηθισμένη τα πράγματα γίνονται πιο απλά. 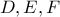 τα ίχνη των ύψων των
τα ίχνη των ύψων των  του αρχικού τριγώνου. Από λόγο μέσων υπάρχει ομοιοθεσία
του αρχικού τριγώνου. Από λόγο μέσων υπάρχει ομοιοθεσία  με κέντρο
με κέντρο  στον
στον 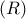 Άρα
Άρα  συνευθειακά όπου
συνευθειακά όπου  το κέντρο
το κέντρο  είναι το κέντρο του κύκλου
είναι το κέντρο του κύκλου  άρα ΑΝ
άρα ΑΝ 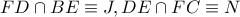 τότε
τότε  Άρα αρκεί
Άρα αρκεί  Και αυτό μας οδηγεί στους ριζικούς άξονες.
Και αυτό μας οδηγεί στους ριζικούς άξονες.  ριζικά κέντρα
ριζικά κέντρα 

 με
με  ,τότε τα τρίγωνα
,τότε τα τρίγωνα  έχουν
έχουν  άρα είναι ίσα ,δηλαδή
άρα είναι ίσα ,δηλαδή  άρα
άρα  παραλληλόγραμμο και
παραλληλόγραμμο και 

 .Είναι
.Είναι  άρα
άρα  εγγράψιμο ,δηλαδή
εγγράψιμο ,δηλαδή 
 .
. (
(
 θα είναι
θα είναι 

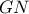 διχοτόμος της
διχοτόμος της 
 εγγράψιμο αρκεί λοιπόν
εγγράψιμο αρκεί λοιπόν 
 τότε
τότε  όπου
όπου  και του περίκυκλου του
και του περίκυκλου του 
 .Έστω
.Έστω  με τον κύκλο
με τον κύκλο 

 συνευθειακά.
συνευθειακά. σημείο του κύκλου
σημείο του κύκλου  .Το OADN' είναι ισοσκελές τραπέζιο και το
.Το OADN' είναι ισοσκελές τραπέζιο και το  παραλληλόγραμμο.Τα τρίγωνα
παραλληλόγραμμο.Τα τρίγωνα  έχουν
έχουν  άρα είναι ίσα και
άρα είναι ίσα και  ,
, 
 τέμνει τον
τέμνει τον  στο
στο  .Επειδή
.Επειδή  και
και  είναι
είναι  μεσοκάθετη του
μεσοκάθετη του  άρα
άρα  και η απόδειξη ολοκληρώθηκε.
και η απόδειξη ολοκληρώθηκε. . Παρατηρούμε ότι
. Παρατηρούμε ότι  συνευθειακά το οποίο θα αποδείξουμε.
συνευθειακά το οποίο θα αποδείξουμε. και
και 
 επίσης
επίσης  με
με 
 οπότε
οπότε 
 άρα KHIJ εγγράψιμο
άρα KHIJ εγγράψιμο παρατηρούμε ότι
παρατηρούμε ότι  συνευθειακά το οποίο θα δείξουμε
συνευθειακά το οποίο θα δείξουμε Άρα Α,I',H' συνευθειακά αφού ανήκουν στη διχοτόμου της
Άρα Α,I',H' συνευθειακά αφού ανήκουν στη διχοτόμου της 
 οπότε K'H'I'J' εγγράψιμο
οπότε K'H'I'J' εγγράψιμο
 είναι ισοσκελές τραπέζιο άρα τα τμήματα
είναι ισοσκελές τραπέζιο άρα τα τμήματα  τα οποία είναι διαγώνιες στα εγρράψιμα που θέλουμε μοιράζονται την ίδια μεσοκάθετη. Λόγο των τόξων KK' και II' έχουμε
τα οποία είναι διαγώνιες στα εγρράψιμα που θέλουμε μοιράζονται την ίδια μεσοκάθετη. Λόγο των τόξων KK' και II' έχουμε  άρα και το
άρα και το  ισοσκελές τραπέζιο άρα και το δεύτερο ζεύγος Διαγωνίων των εγγράψιμων μοιράζεται την ίδια μεσοκάθετη οπότε τα εγγράψιμα
ισοσκελές τραπέζιο άρα και το δεύτερο ζεύγος Διαγωνίων των εγγράψιμων μοιράζεται την ίδια μεσοκάθετη οπότε τα εγγράψιμα 
 προκύπτουν αμέσως ως εξής(βάζω και το σχήμα για να υπάρχει):
προκύπτουν αμέσως ως εξής(βάζω και το σχήμα για να υπάρχει):