Θέματα της δεύτερης φάσης (τελικής) για την 10η τάξη
[/i]
[b]1.[/b] Για την μη σταθερή αριθμητική πρόοδο
 υπάρχει τέτοιος μη μηδενικός φυσικός αριθμός
υπάρχει τέτοιος μη μηδενικός φυσικός αριθμός  , ώστε
, ώστε  .
.Να αποδείξετε, ότι σε αυτή την πρόοδο δεν υπάρχουν μηδενικοί όροι. [size=85](Σ. Ιβάνοβ)[/size]
[b]2.[/b] Κάθε δυο πόλεις, από
 , της Ρουριτανίας είναι συνδεμένες με απευθείας αερογραμμή με μια εκ δυο εταιριών. Φίλο μονοπωλιακή επιτροπή θέλει, τουλάχιστον
, της Ρουριτανίας είναι συνδεμένες με απευθείας αερογραμμή με μια εκ δυο εταιριών. Φίλο μονοπωλιακή επιτροπή θέλει, τουλάχιστον  διαδρομές να εκτελούνται από την ίδια εταιρία. Για αυτό της επιτρέπεται ακόμη και κάθε μέρα να διαλέξει οποιεσδήποτε τρεις πόλεις και να αλλάξει την δικαιοδοσία τριών διαδρομών, που συνδέουν αυτές τις πόλεις μεταξύ τους (δηλαδή να αφαιρέσει αυτές τις διαδρομές από την μια εταιρία, η οποία τις εκτελεί, και να τις αναθέσει στην άλλη). Για ποιο μέγιστο
διαδρομές να εκτελούνται από την ίδια εταιρία. Για αυτό της επιτρέπεται ακόμη και κάθε μέρα να διαλέξει οποιεσδήποτε τρεις πόλεις και να αλλάξει την δικαιοδοσία τριών διαδρομών, που συνδέουν αυτές τις πόλεις μεταξύ τους (δηλαδή να αφαιρέσει αυτές τις διαδρομές από την μια εταιρία, η οποία τις εκτελεί, και να τις αναθέσει στην άλλη). Για ποιο μέγιστο  η επιτροπή εγγυημένα σε κάποιο χρονικό διάστημα θα μπορέσει να επιτύχει το σκοπό της, ανεξάρτητα το πως είναι κατανεμημένες οι διαδρομές την τρέχουσα στιγμή; [size=85](Σ. Μπερλόβ)[/size]
η επιτροπή εγγυημένα σε κάποιο χρονικό διάστημα θα μπορέσει να επιτύχει το σκοπό της, ανεξάρτητα το πως είναι κατανεμημένες οι διαδρομές την τρέχουσα στιγμή; [size=85](Σ. Μπερλόβ)[/size][b]3.[/b] Δίνονται οι μη μηδενικοί φυσικοί αριθμοί
 και
και  . Να δείξετε, ότι
. Να δείξετε, ότι  .
. [size=85](Α.Χράμπροβ)[/size]
[b]4.[/b] Δίνεται κυρτό τετράπλευρο
 . Οι διάμεσοι του τριγώνου
. Οι διάμεσοι του τριγώνου  τέμνονται στο σημείο
τέμνονται στο σημείο  και οι διάμεσοι του τριγώνου
και οι διάμεσοι του τριγώνου  , στο σημείο
, στο σημείο  . Ο περιγεγραμμένος κύκλος του τριγώνου
. Ο περιγεγραμμένος κύκλος του τριγώνου  , τέμνει το ευθύγραμμο τμήμα
, τέμνει το ευθύγραμμο τμήμα  στο σημείο
στο σημείο  , εσωτερικό του τριγώνου
, εσωτερικό του τριγώνου 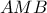 . Είναι γνωστό, ότι
. Είναι γνωστό, ότι  . Να αποδείξετε, ότι
. Να αποδείξετε, ότι  . [size=85](Α.Κουζνέτσοβ, Ρ. Κουζνέτσοβ)
. [size=85](Α.Κουζνέτσοβ, Ρ. Κουζνέτσοβ)[/size]
[i]Καταληκτική αίθουσα[/i]
[b]5.[/b] Μια τάξη έχει
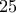 μαθητές. Ο δάσκαλος θέλει να προμηθευτεί
μαθητές. Ο δάσκαλος θέλει να προμηθευτεί  σοκολάτες, να διεξάγει μια ολυμπιάδα και να μοιράσει για την επιτυχία των μαθητών όλες τις
σοκολάτες, να διεξάγει μια ολυμπιάδα και να μοιράσει για την επιτυχία των μαθητών όλες τις  σοκολάτες (οι λύσαντες ίσο αριθμό προβλημάτων λαμβάνουν ίσο αριθμό, οι λύσαντες λιγότερο, λιγότερες, πιθανόν και μηδενικό αριθμό σοκολάτων ). Για ποιο ελάχιστο
σοκολάτες (οι λύσαντες ίσο αριθμό προβλημάτων λαμβάνουν ίσο αριθμό, οι λύσαντες λιγότερο, λιγότερες, πιθανόν και μηδενικό αριθμό σοκολάτων ). Για ποιο ελάχιστο  αυτό είναι δυνατόν ανεξάρτητα από τον αριθμό των προβλημάτων της ολυμπιάδας και της επίδοσης των μαθητών; [size=85](Μ.Αντίνοβ)[/size]
αυτό είναι δυνατόν ανεξάρτητα από τον αριθμό των προβλημάτων της ολυμπιάδας και της επίδοσης των μαθητών; [size=85](Μ.Αντίνοβ)[/size][b]6.[/b] Είναι δυνατόν άραγε σε όλα τα κελιά ενός άπειρου τετραγωνισμένου επιπέδου να τοποθετήσουμε όλους του θετικούς ακέραιους (από μια φορά) έτσι, ώστε για κάθε
 το άθροισμα των αριθμών σε κάθε
το άθροισμα των αριθμών σε κάθε  τετράγωνο να διαιρείτε με τον
τετράγωνο να διαιρείτε με τον  ; [size=85](Α.Γκολοβάνοβ)
; [size=85](Α.Γκολοβάνοβ)[/size]
[b]7.[/b] Σε τετράγωνο
 σημειώθηκαν
σημειώθηκαν  σημεία. Να αποδείξετε, ότι θα βρεθεί παραλληλόγραμμο, με πλευρές παράλληλες προς τις πλευρές του τετραγώνου, το εμβαδόν του οποίου διαφέρει από το πλήθος των σημείων που είναι τοποθετημένα σε αυτό τουλάχιστον κατά
σημεία. Να αποδείξετε, ότι θα βρεθεί παραλληλόγραμμο, με πλευρές παράλληλες προς τις πλευρές του τετραγώνου, το εμβαδόν του οποίου διαφέρει από το πλήθος των σημείων που είναι τοποθετημένα σε αυτό τουλάχιστον κατά  . [size=85](Α.Χράμπροβ)[/size]
. [size=85](Α.Χράμπροβ)[/size][url=http://www.pdmi.ras.ru/~olymp/]Πηγή η επίσημη σελίδα της ολυμπιάδας.[/url]




 με
με 



 λόγο της αριθμητικής προόδου όμως
λόγο της αριθμητικής προόδου όμως  ακέραιοι μεγαλύτεροι ή ίσου του 1 και αυτό σημαίνει πως στην τελαυταία ισότητα που έχουμε το αριστερό μέλος είναι αρνητικό ή ίσο με το 0 και το δεξί θετικός το οποίο είναι άτοπο. Οπότε δεν υπάρχει μηδενικός όρος στην αριθμητική πρόοδο.
ακέραιοι μεγαλύτεροι ή ίσου του 1 και αυτό σημαίνει πως στην τελαυταία ισότητα που έχουμε το αριστερό μέλος είναι αρνητικό ή ίσο με το 0 και το δεξί θετικός το οποίο είναι άτοπο. Οπότε δεν υπάρχει μηδενικός όρος στην αριθμητική πρόοδο.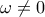 η διαφορά της προόδου, και
η διαφορά της προόδου, και  ο πρώτος όρος. Η δοσμένη γράφεται (εύκολο)
ο πρώτος όρος. Η δοσμένη γράφεται (εύκολο)  (1) (υπέθεσα ότι
(1) (υπέθεσα ότι  ).
). , τότε
, τότε  .
.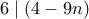 , άτοπο, αφού
, άτοπο, αφού  .
. . Θα δείξω ότι το
. Θα δείξω ότι το  είναι εγγράψιμο. Έστω
είναι εγγράψιμο. Έστω  το μέσον της
το μέσον της  , και
, και  .
. και
και 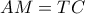 .
. (τα
(τα  είναι βαρύκεντρα), επομένως
είναι βαρύκεντρα), επομένως  , επομένως
, επομένως  , αφού
, αφού  .
. , από το παραλληλόγραμμο
, από το παραλληλόγραμμο  . Συνεπώς,
. Συνεπώς,  ισοσκελές τραπέζιο, οπότε και εγγράψιμο.
ισοσκελές τραπέζιο, οπότε και εγγράψιμο. , και η απόδειξη ολοκληρώθηκε.
, και η απόδειξη ολοκληρώθηκε. , οπότε αν
, οπότε αν 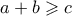 , είναι
, είναι  .
. . Γράφω την ανισότητα ως
. Γράφω την ανισότητα ως  .
. και θα δείξω ότι είναι γνησίως φθίνουσα.
και θα δείξω ότι είναι γνησίως φθίνουσα. , και αρκεί
, και αρκεί  , και αφού
, και αφού  , ή αλλιώς
, ή αλλιώς 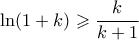 , όπου
, όπου  .
.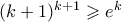 . Αν
. Αν  , η προηγούμενη είναι προφανής.
, η προηγούμενη είναι προφανής. , και
, και  οπότε αρκεί
οπότε αρκεί  . Θέτω
. Θέτω  , οπότε αρκεί
, οπότε αρκεί  , και αφού
, και αφού  .
. είναι φθίνουσα, οπότε
είναι φθίνουσα, οπότε  , και αρκεί μετά από πράξεις να δείξω ότι
, και αρκεί μετά από πράξεις να δείξω ότι  , που είναι προφανές.
, που είναι προφανές. , και αφού
, και αφού  , είναι από την Bernoulli,
, είναι από την Bernoulli,  .
.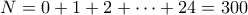 σοκολάτες.
σοκολάτες. μαθητές οι οποίοι έχουν τον χαμηλότερο βαθμό,
μαθητές οι οποίοι έχουν τον χαμηλότερο βαθμό,  με το δεύτερο χαμηλότερο βαθμό κ.ο.κ. μέχρι τους
με το δεύτερο χαμηλότερο βαθμό κ.ο.κ. μέχρι τους  μαθητές με τον ψηλότερο βαθμό. Τότε έχουμε
μαθητές με τον ψηλότερο βαθμό. Τότε έχουμε  . Ο δάσκαλος μπορεί να δώσει
. Ο δάσκαλος μπορεί να δώσει  σοκολάτες σε αυτούς με τον χαμηλότερο βαθμό, από μία σε αυτούς με τον δεύτερο χαμηλότερο κ.ο.κ. Συνολικά θα χρειαστεί:
σοκολάτες σε αυτούς με τον χαμηλότερο βαθμό, από μία σε αυτούς με τον δεύτερο χαμηλότερο κ.ο.κ. Συνολικά θα χρειαστεί:

 όπως ισχυριστήκαμε.
όπως ισχυριστήκαμε.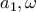 είναι ακέραιοι. Οπότε από την
είναι ακέραιοι. Οπότε από την  δεν μπορούμε να συμπεράνουμε ότι
δεν μπορούμε να συμπεράνουμε ότι 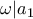 . Λύνοντας όμως ως προς
. Λύνοντας όμως ως προς  και αντικαθιστώντας στην (1) καταλήγουμε στο
και αντικαθιστώντας στην (1) καταλήγουμε στο  οπότε πάλι καταλήγουμε προς άτοπο όπως στη λύση του Ορέστη.
οπότε πάλι καταλήγουμε προς άτοπο όπως στη λύση του Ορέστη. .
. .
.  ζεύγη πόλεων και βάλουμε μεταξύ των πόλεων των ζευγών μία διαδρομή από την αντίπαλη εταιρεία, τότε ότι και να κάνουμε μετά, σε κάθε μία από αυτές τις
ζεύγη πόλεων και βάλουμε μεταξύ των πόλεων των ζευγών μία διαδρομή από την αντίπαλη εταιρεία, τότε ότι και να κάνουμε μετά, σε κάθε μία από αυτές τις  πόλεις θα υπάρχει πάντα τουλάχιστον μία διαδρομή από την αντίπαλη εταιρεία. Άρα η αντίπαλη εταιρεία θα έχει πάντα τουλάχιστον
πόλεις θα υπάρχει πάντα τουλάχιστον μία διαδρομή από την αντίπαλη εταιρεία. Άρα η αντίπαλη εταιρεία θα έχει πάντα τουλάχιστον  με δύο ή περισσότερες διαδρομές της αντίπαλης εταιρείας. Αυτό ισχύει διότι αν έχουμε διαδρομές
με δύο ή περισσότερες διαδρομές της αντίπαλης εταιρείας. Αυτό ισχύει διότι αν έχουμε διαδρομές  και
και  , οι διαδρομές της αντίπαλης εταιρείας μειώνονται τουλάχιστον κατά μία, άτοπο.
, οι διαδρομές της αντίπαλης εταιρείας μειώνονται τουλάχιστον κατά μία, άτοπο. στο οποίο είναι σημειωμένα
στο οποίο είναι σημειωμένα  σημεία όπου
σημεία όπου  . Υποθέτουμε ότι
. Υποθέτουμε ότι  .
. τετράγωνο μέσα στο ορθογώνιο. Αν δεν υπάρχουν σημεία μέσα σε αυτό, τότε είναι καλό και τελειώσαμε. Αλλιώς παίρνουμε ένα σημείο μέσα στο τετράγωνο και το χρησιμοποιούμε για να χωρίσουμε το
τετράγωνο μέσα στο ορθογώνιο. Αν δεν υπάρχουν σημεία μέσα σε αυτό, τότε είναι καλό και τελειώσαμε. Αλλιώς παίρνουμε ένα σημείο μέσα στο τετράγωνο και το χρησιμοποιούμε για να χωρίσουμε το  άλλα ορθογώνια. Το άθροισμα των εμβαδών τους είναι ίσο με
άλλα ορθογώνια. Το άθροισμα των εμβαδών τους είναι ίσο με  ενώ το πλήθος των σημείων μέσα σε αυτά είναι τουλάχιστον
ενώ το πλήθος των σημείων μέσα σε αυτά είναι τουλάχιστον  επειδή το σημείο που πήραμε ανήκει και στα τέσσερα ορθογώνια. Άρα τουλάχιστον ένα από αυτά τα τέσσερα μικρότερα ορθογώνια έχει διαστάσεις
επειδή το σημείο που πήραμε ανήκει και στα τέσσερα ορθογώνια. Άρα τουλάχιστον ένα από αυτά τα τέσσερα μικρότερα ορθογώνια έχει διαστάσεις 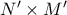 και
και  σημειωμένα σημεία με
σημειωμένα σημεία με  . Επιπλέον έχουμε
. Επιπλέον έχουμε  και
και  .
. και
και  . Είτε θα βρούμε ένα καλό τετράγωνο είτε θα πάρουμε ένα
. Είτε θα βρούμε ένα καλό τετράγωνο είτε θα πάρουμε ένα  ορθογώνιο με
ορθογώνιο με  και
και  . Μέσα σε αυτό είτε θα βρούμε ένα καλό τετράγωνο, είτε θα πάρουμε ένα
. Μέσα σε αυτό είτε θα βρούμε ένα καλό τετράγωνο, είτε θα πάρουμε ένα  ορθογώνιο με
ορθογώνιο με  και
και  . Επαναλαμβάνοντας άλλες
. Επαναλαμβάνοντας άλλες 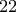 φορές, είτε θα έχουμε βρει ένα καλό τετράγωνο είτε θα καταλήξουμε σε ένα
φορές, είτε θα έχουμε βρει ένα καλό τετράγωνο είτε θα καταλήξουμε σε ένα  ορθογώνιο με
ορθογώνιο με 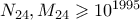 και
και  . Αυτό όμως είναι ένα καλό ορθογώνιο οπότε τελειώσαμε.
. Αυτό όμως είναι ένα καλό ορθογώνιο οπότε τελειώσαμε. . Το σχόλιο είναι: "Αν και το πρόβλημα ισχύει, είναι αρκετά δύσκλο για την θέση που βρίσκεται. Καλύτερα θεωρείστε
. Το σχόλιο είναι: "Αν και το πρόβλημα ισχύει, είναι αρκετά δύσκλο για την θέση που βρίσκεται. Καλύτερα θεωρείστε 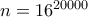 ".
".