1. Για τους πραγματικούς αριθμούς
 και
και  είναι γνωστό, ότι
είναι γνωστό, ότι  ,
,  . Για ποιους αριθμούς
. Για ποιους αριθμούς  μπορούμε να ισχυριστούμε, ότι τουλάχιστον ένας εκ των αριθμών
μπορούμε να ισχυριστούμε, ότι τουλάχιστον ένας εκ των αριθμών  ισούται με
ισούται με  ; (Να βρείτε όλους τους τέτοιους
; (Να βρείτε όλους τους τέτοιους  και αποδείξτε, ότι δεν υπάρχουν άλλοι.)
και αποδείξτε, ότι δεν υπάρχουν άλλοι.)2. Ο κύριος
 για μια ώρα στάθηκε στο σημείο με συντεταγμένες
για μια ώρα στάθηκε στο σημείο με συντεταγμένες  . Κατά την διάρκεια της ίδιας ώρας, κινήθηκε ευθύγραμμα και ομαλά, ο κύριος
. Κατά την διάρκεια της ίδιας ώρας, κινήθηκε ευθύγραμμα και ομαλά, ο κύριος  από το σημείο
από το σημείο  προς το σημείο
προς το σημείο  . Κατά την ίδια ώρα η δεσποινίς
. Κατά την ίδια ώρα η δεσποινίς  , επίσης κινούμενη ευθύγραμμα και ομαλά, μετακινήθηκε από το σημείο
, επίσης κινούμενη ευθύγραμμα και ομαλά, μετακινήθηκε από το σημείο  στο
στο  . Πόσες φορές κατά την διάρκεια της παραπάνω χρονικής παρατήρησης το εμβαδόν του τριγώνου
. Πόσες φορές κατά την διάρκεια της παραπάνω χρονικής παρατήρησης το εμβαδόν του τριγώνου  έλαβε ακέραια τιμή; Η αρχική και τελική στιγμή συμπεριλαμβάνονται.
έλαβε ακέραια τιμή; Η αρχική και τελική στιγμή συμπεριλαμβάνονται.3. Από
 κανονικά εξάγωνα πλευράς
κανονικά εξάγωνα πλευράς  σχηματίστηκε πολύγωνο στο επίπεδο, «κολλώντας» τα εξάγωνα κατά πλευρά. Οποιαδήποτε δυο εξάγωνα είτε έχουν ακριβώς μια κοινή πλευρά, είτε δεν έχουν καθόλου κοινά σημεία. Στο εσωτερικό του πολυγώνου δεν υπάρχουν τρύπες. Εξάλλου κάθε εξάγωνου τουλάχιστον μια πλευρά βρίσκεται στο σύνορο του πολυγώνου. Ποια είναι η ελάχιστη περίμετρος που μπορεί να έχει το πολύγωνο υπό τις παραπάνω συνθήκες;
σχηματίστηκε πολύγωνο στο επίπεδο, «κολλώντας» τα εξάγωνα κατά πλευρά. Οποιαδήποτε δυο εξάγωνα είτε έχουν ακριβώς μια κοινή πλευρά, είτε δεν έχουν καθόλου κοινά σημεία. Στο εσωτερικό του πολυγώνου δεν υπάρχουν τρύπες. Εξάλλου κάθε εξάγωνου τουλάχιστον μια πλευρά βρίσκεται στο σύνορο του πολυγώνου. Ποια είναι η ελάχιστη περίμετρος που μπορεί να έχει το πολύγωνο υπό τις παραπάνω συνθήκες;4. Από τις κορυφές του τριγώνου
 άγονται τρεις παράλληλες ευθείες
άγονται τρεις παράλληλες ευθείες  αντίστοιχα, μη παράλληλες προς τις πλευρές του τριγώνου. Έστω
αντίστοιχα, μη παράλληλες προς τις πλευρές του τριγώνου. Έστω  τα μέσα των πλευρών
τα μέσα των πλευρών  και
και  τα σημεία τομής του ζεύγους ευθείων
τα σημεία τομής του ζεύγους ευθείων  και
και  ,
,  και
και  ,
,  και
και  αντίστοιχα. Να αποδείξετε, ότι οι ευθείες
αντίστοιχα. Να αποδείξετε, ότι οι ευθείες 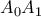 ,
, 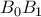 και
και  διέρχονται από το ίδιο σημείο.
διέρχονται από το ίδιο σημείο.5. Θεωρούμε όλα τα δυνατά τριώνυμα δευτέρου βαθμού
 με ακέραιους συντελεστές
με ακέραιους συντελεστές  και
και  . Θα ονομάσουμε σύνολο τιμών ενός τέτοιου τριωνύμου το σύνολο των τιμών που μπορεί να πάρει σε ακέραια σημεία
. Θα ονομάσουμε σύνολο τιμών ενός τέτοιου τριωνύμου το σύνολο των τιμών που μπορεί να πάρει σε ακέραια σημεία 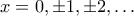 Ποιος είναι ο μέγιστος αριθμός τέτοιων τριωνύμων που μπορούμε να διαλέξουμε, ώστε τα σύνολα τιμών τους ανά δυο να είναι ξένα μεταξύ τους.
Ποιος είναι ο μέγιστος αριθμός τέτοιων τριωνύμων που μπορούμε να διαλέξουμε, ώστε τα σύνολα τιμών τους ανά δυο να είναι ξένα μεταξύ τους.6. Η ακολουθία αριθμών
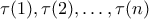 ονομάζεται μετάθεση μήκους
ονομάζεται μετάθεση μήκους  , αν ο καθένας εκ των αριθμών
, αν ο καθένας εκ των αριθμών  συναντάται σε αυτή την ακολουθία ακριβώς από μια φορά. Για παράδειγμα,
συναντάται σε αυτή την ακολουθία ακριβώς από μια φορά. Για παράδειγμα,  είναι μια μετάθεση μήκους
είναι μια μετάθεση μήκους  . Να βρείτε όλα τα
. Να βρείτε όλα τα  , για τα οποία θα βρεθεί μετάθεση
, για τα οποία θα βρεθεί μετάθεση 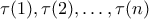 , που ικανοποιεί τις τέσσερις συνθήκες:
, που ικανοποιεί τις τέσσερις συνθήκες: Οι αριθμοί
Οι αριθμοί  για όλα τα
για όλα τα  από
από  έως
έως  συμπεριλαμβανομένου έχουν ανά δύο διαφορετικά υπόλοιπα στη διαίρεση με το
συμπεριλαμβανομένου έχουν ανά δύο διαφορετικά υπόλοιπα στη διαίρεση με το  .
.  Οι αριθμοί
Οι αριθμοί  για όλα τα
για όλα τα  από
από  έως
έως  συμπεριλαμβανομένου έχουν ανά δύο διαφορετικά υπόλοιπα στη διαίρεση με το
συμπεριλαμβανομένου έχουν ανά δύο διαφορετικά υπόλοιπα στη διαίρεση με το  .
. Οι αριθμοί
Οι αριθμοί  για όλα τα
για όλα τα  από
από  έως
έως  συμπεριλαμβανομένου έχουν ανά δύο διαφορετικά υπόλοιπα στη διαίρεση με το
συμπεριλαμβανομένου έχουν ανά δύο διαφορετικά υπόλοιπα στη διαίρεση με το  .
. Οι αριθμοί
Οι αριθμοί  για όλα τα
για όλα τα  από
από  έως
έως  συμπεριλαμβανομένου έχουν ανά δύο διαφορετικά υπόλοιπα στη διαίρεση με το
συμπεριλαμβανομένου έχουν ανά δύο διαφορετικά υπόλοιπα στη διαίρεση με το  .
.(*) Η ολυμπιάδα «Υψηλά πρότυπα» διοργανώνεται από την «Ανώτατη Σχολή Οικονομικών» του Εθνικού Ερευνητικού Πανεπιστημίου της Ρωσίας και εντάσσεται σε ένα σύνολο εισαγωγικού τύπου ολυμπιάδων που δίνει έξτρα μόρια στους υποψήφιους για την τριτοβάθμια εκπαίδευση. Παρόλο που κανονικά θα λέγαμε ότι ανήκει στο φάκελο «Διάφορα άλλα θέματα εξετάσεων», λόγω της φύσης των θεμάτων θεώρησα ότι θα ήταν καλύτερα να τοποθετηθεί στον παρόν φάκελο.
Πηγή

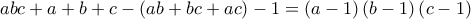


 η οποία όμως έχει άπειρες λύσεις ,άρα ο μόνος
η οποία όμως έχει άπειρες λύσεις ,άρα ο μόνος 

 . Τότε με
. Τότε με  το μέσο της
το μέσο της  και
και  θα είναι και
θα είναι και  οπότε με
οπότε με  το μέσο της
το μέσο της  και
και  (από το ευθύγραμμο τμήμα που συνδέει τα μέσα δύο πλευρών τριγώνου…) προκύπτει από το Θεώρημα της κεντρικής δέσμης (με κέντρο το
(από το ευθύγραμμο τμήμα που συνδέει τα μέσα δύο πλευρών τριγώνου…) προκύπτει από το Θεώρημα της κεντρικής δέσμης (με κέντρο το  ) ότι
) ότι  είναι συνευθειακά.
είναι συνευθειακά. 
 και
και  το μέσο της
το μέσο της  προκύπτει ότι η δέσμη
προκύπτει ότι η δέσμη  είναι αρμονική και για παρόμοιο λόγο προκύπτει ότι και η δέσμη
είναι αρμονική και για παρόμοιο λόγο προκύπτει ότι και η δέσμη  είναι αρμονική.
είναι αρμονική. 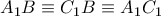 προκύπτει ότι τα σημεία τομής των ομολόγων άλλων τριών ακτινών τους είναι συνευθειακά, δηλαδή τα
προκύπτει ότι τα σημεία τομής των ομολόγων άλλων τριών ακτινών τους είναι συνευθειακά, δηλαδή τα  είναι συνευθειακά ή ισοδύναμα οι ευθείες
είναι συνευθειακά ή ισοδύναμα οι ευθείες  διέρχονται από το ίδιο σημείο (εδώ το
διέρχονται από το ίδιο σημείο (εδώ το  ) και το ζητούμενο έχει αποδειχθεί.
) και το ζητούμενο έχει αποδειχθεί. και
και  οι θέσεις των ατόμων μία χρονική στιγμή
οι θέσεις των ατόμων μία χρονική στιγμή  (σε λεπτά).
(σε λεπτά). οι ταχύτητες των
οι ταχύτητες των 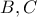 αντίστοιχα.
αντίστοιχα.

 ' είναι της μορφής
' είναι της μορφής  .Άρα:
.Άρα:



![\left ( AB_1C_1 \right )=\left ( AC_1L \right )-\left ( AB_1E \right )-\left ( B_1C_1LE \right )=\dfrac{\left ( 4+\dfrac{t}{3} \right )\left ( 30-\dfrac{t}{2} \right )}{2}-\dfrac{\dfrac{t}{3}\left ( 22-\dfrac{t}{3} \right )}{2}-\dfrac{\left ( 4+\dfrac{t}{3}+\dfrac{t}{3} \right )\left [\left ( 30-\dfrac{t}{2} \right )-\left ( 22-\dfrac{t}{3} \right ) \right ]}{2}=....=\boxed{\dfrac{t^2}{36}-2t+44} \left ( AB_1C_1 \right )=\left ( AC_1L \right )-\left ( AB_1E \right )-\left ( B_1C_1LE \right )=\dfrac{\left ( 4+\dfrac{t}{3} \right )\left ( 30-\dfrac{t}{2} \right )}{2}-\dfrac{\dfrac{t}{3}\left ( 22-\dfrac{t}{3} \right )}{2}-\dfrac{\left ( 4+\dfrac{t}{3}+\dfrac{t}{3} \right )\left [\left ( 30-\dfrac{t}{2} \right )-\left ( 22-\dfrac{t}{3} \right ) \right ]}{2}=....=\boxed{\dfrac{t^2}{36}-2t+44}](/forum/ext/geomar/texintegr/latexrender/pictures/b74fa725ea81482dbf8b7e6ce69e54c1.png)
 έχει
έχει 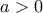 και παρουσιάζει ελάχιστο το
και παρουσιάζει ελάχιστο το  και παίρνει όλες τις ακέραιες τιμές από το
και παίρνει όλες τις ακέραιες τιμές από το  μέχρι το
μέχρι το  στο οποίο ελαχιστοποιείται και μετά φθάνει εως και το
στο οποίο ελαχιστοποιείται και μετά φθάνει εως και το 
 φορές.
φορές.![t \in [0,1] t \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/dff6e05ec00b53d46e366975136d0d2e.png) έχουμε
έχουμε  και
και  . Για το εμβαδόν μπορούμε να χρησιμοποιήσουμε τον τύπο της ορίζουσας. Το εμβαδόν ισούται με
. Για το εμβαδόν μπορούμε να χρησιμοποιήσουμε τον τύπο της ορίζουσας. Το εμβαδόν ισούται με  όπου
όπου 
 .
.  είναι ακέραιος. Ισοδύναμα θέλουμε
είναι ακέραιος. Ισοδύναμα θέλουμε  για
για ![10t-6 \in [-6,4] 10t-6 \in [-6,4]](/forum/ext/geomar/texintegr/latexrender/pictures/467e03eb273418dd0d9b934da5bcf14c.png) πρέπει
πρέπει  . Έχουμε λοιπόν
. Έχουμε λοιπόν  διαφορετικές τιμές του
διαφορετικές τιμές του