[b]1.[/b] Ο Πέτρος και ο Βασίλης παίζουν ένα παιχνίδι. Τα παιδιά με την σειρά (ξεκινάει ο Πέτρος) σημειώνουν μη μηδενικούς φυσικούς αριθμούς, που δεν υπερβαίνουν το 1000. Δεν επιτρέπεται να σημειώσουν έναν ήδη σημειωμένο αριθμό, καθώς και οποιοδήποτε αριθμό που διαφέρει από κάποιο σημειωμένο κατά 1 ή που να δίνει με κάποιο σημειωμένο άθροισμα 1001. Αυτός που δεν μπορεί να κάνει κίνηση, χάνει. Ποιος έχει στρατηγική νίκης;
[b]2.[/b] Το πολυώνυμο
 τετάρτου βαθμού είναι τέτοιο, ώστε η εξίσωση
τετάρτου βαθμού είναι τέτοιο, ώστε η εξίσωση  να έχει τέσσερις ρίζες, αλλά οποιαδήποτε εξίσωση της μορφής
να έχει τέσσερις ρίζες, αλλά οποιαδήποτε εξίσωση της μορφής  , το πολύ δυο. Να αποδείξετε, ότι και η εξίσωση
, το πολύ δυο. Να αποδείξετε, ότι και η εξίσωση  έχει το πολύ δυο ρίζες.
έχει το πολύ δυο ρίζες.[b]3.[/b] Θα ονομάσουμε τον μη μηδενικό φυσικό αριθμό «καλό», αν μπορεί να αναπαρασταθεί ως άθροισμα δυο πρώτων μεταξύ τους φυσικών αριθμών, ο πρώτος εκ των οποίων γράφεται σαν γινόμενο περιττού πλήθους πρώτων αριθμών (όχι απαραίτητα διαφορετικών) και ο δεύτερος ως άρτιου. Να αποδείξετε, ότι υπάρχουν άπειροι καλοί που είναι τέταρτες δυνάμεις φυσικών αριθμών.
[b]4.[/b] Η διάμεσος
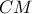 του τριγώνου
του τριγώνου  ισούται με την διχοτόμο
ισούται με την διχοτόμο  ,
,  . Να αποδείξετε, ότι το τρίγωνο είναι ισόπλευρο.
. Να αποδείξετε, ότι το τρίγωνο είναι ισόπλευρο.[b]5.[/b] Δίνεται τετράγωνο
 . Τα κελία του οποίου χρωματίζονται με
. Τα κελία του οποίου χρωματίζονται με  χρώματα έτσι, ώστε σε κάθε στήλη και κάθε γραμμή τα χρώματα όλων των κελιών να είναι διαφορετικά. Καμία τετράδα κελιών που βρίσκεται στην τομή δυο γραμμών και δυο στηλών, δεν μπορεί να είναι χρωματισμένη με ακριβώς τρία χρώματα. Με τι μπορεί να ισούται το
χρώματα έτσι, ώστε σε κάθε στήλη και κάθε γραμμή τα χρώματα όλων των κελιών να είναι διαφορετικά. Καμία τετράδα κελιών που βρίσκεται στην τομή δυο γραμμών και δυο στηλών, δεν μπορεί να είναι χρωματισμένη με ακριβώς τρία χρώματα. Με τι μπορεί να ισούται το  ;
;[b]6.[/b] Οι θετικοί αριθμοί
 είναι τέτοιοι, ώστε
είναι τέτοιοι, ώστε  . Να αποδείξετε, ότι
. Να αποδείξετε, ότι 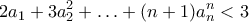 .
.[b]7.[/b] Στο εσωτερικό τριγώνου
 δίνεται κύκλος. Από το σημείο
δίνεται κύκλος. Από το σημείο  προς αυτό το κύκλο άγονται δυο εφαπτόμενες, οι οποίες τέμνουν την πλευρά
προς αυτό το κύκλο άγονται δυο εφαπτόμενες, οι οποίες τέμνουν την πλευρά  στα σημεία
στα σημεία  και
και  . Τα σημεία
. Τα σημεία  ορίζονται αναλόγως. Είναι γνωστό, ότι πέντε από αυτά τα σημεία είναι ομοκυκλικά. Να αποδείξετε, ότι και το έκτο θα ανήκει σε αυτό το κύκλο.
ορίζονται αναλόγως. Είναι γνωστό, ότι πέντε από αυτά τα σημεία είναι ομοκυκλικά. Να αποδείξετε, ότι και το έκτο θα ανήκει σε αυτό το κύκλο.[b]8.[/b] Δίνεται φυσικός αριθμός
 . Να αποδείξετε, ότι στις ακμές πλήρους γράφου
. Να αποδείξετε, ότι στις ακμές πλήρους γράφου  κόμβων μπορούμε να τοποθετήσουμε τους αριθμούς
κόμβων μπορούμε να τοποθετήσουμε τους αριθμούς  από μια φορά έτσι, ώστε σε κάθε (πιθανόν κλειστή) διαδρομή τριών ακμών το άθροισμα των αριθμών να είναι τουλάχιστον
από μια φορά έτσι, ώστε σε κάθε (πιθανόν κλειστή) διαδρομή τριών ακμών το άθροισμα των αριθμών να είναι τουλάχιστον  .
.[url=http://www.239.ru/mathcenter?page=1]Πηγή
[/url]

 (γνωστό, προκύπτει με νόμο Συνημιτόνων στα τρίγωνα
(γνωστό, προκύπτει με νόμο Συνημιτόνων στα τρίγωνα  ) και
) και  .
. (1).
(1). , οπότε από
, οπότε από  , ή ισοδύναμα
, ή ισοδύναμα  (2).
(2). και άρα οι (1), (2) γίνονται :
και άρα οι (1), (2) γίνονται : (3) και
(3) και (4).
(4). , και η (3) ξαναγράφεται (μετά την απλοποιήση με το
, και η (3) ξαναγράφεται (μετά την απλοποιήση με το 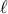 ),
),  (5).
(5). η συνάρτηση του πρώτου μέλους ως προς το
η συνάρτηση του πρώτου μέλους ως προς το  .
. είναι γνησίως αύξουσα.
είναι γνησίως αύξουσα. . Τότε,
. Τότε,  , οπότε
, οπότε  .
. , οπότε
, οπότε  , συνεπώς
, συνεπώς  , και το ζητούμενο δείχθηκε.
, και το ζητούμενο δείχθηκε. . Τότε, ομοίως
. Τότε, ομοίως  .
. , άρα
, άρα  και πάλι
και πάλι 


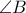 άρα
άρα 
 :
:
 :
:

 (1)
(1) έχουμε:
έχουμε: 
 :
:
 άρα τα τρίγωνα
άρα τα τρίγωνα  είναι ίσα(2)
είναι ίσα(2)
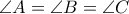
 είναι ορθογώνια. Αυτό όμως, πρέπει να αποδειχθεί.
είναι ορθογώνια. Αυτό όμως, πρέπει να αποδειχθεί. (σύνολο
(σύνολο  αριθμοί) την ανισότητα αριθμητικού-γεωμετρικού μέσου. Προκύπτει η ανισότητα
αριθμοί) την ανισότητα αριθμητικού-γεωμετρικού μέσου. Προκύπτει η ανισότητα .
. θέτουμε στη θέση του
θέτουμε στη θέση του  τον αριθμό
τον αριθμό  . Αθροίζοντας όλες τις τέτοιες ανισότητες λαμβάνουμε
. Αθροίζοντας όλες τις τέτοιες ανισότητες λαμβάνουμε
 το αριστερό μέλος της προς απόδειξης ανίσωσης. Από την εκφώνηση όμως
το αριστερό μέλος της προς απόδειξης ανίσωσης. Από την εκφώνηση όμως  .
. 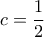 και τότε
και τότε  .
. και παίρνω μεταβλητό σημείο
και παίρνω μεταβλητό σημείο  .
.![A_{2] A_{2]](/forum/ext/geomar/texintegr/latexrender/pictures/4cdec90c530cb0f0886c3430693c8d53.png) ως την τομή της δεύτερης εφαπτομένης από το
ως την τομή της δεύτερης εφαπτομένης από το  .
. και την εγγεγραμμένη του κωνική,υπάρχει ενέλιξη που ανταλλάζει τις
και την εγγεγραμμένη του κωνική,υπάρχει ενέλιξη που ανταλλάζει τις  .
. βρίσκονται σε ενέλιξη στην
βρίσκονται σε ενέλιξη στην  θέλω να δείξω πως περνά και από το
θέλω να δείξω πως περνά και από το 
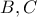 ,ενώ αν πάρω τις τομές των
,ενώ αν πάρω τις τομές των  με την
με την  που είναι συζυγή σημεία της πρώτης ενέλιξης
που είναι συζυγή σημεία της πρώτης ενέλιξης για τα οποία είναι γνωστό πως υπάρχει κωνική που περνά από τις κορυφές τους (πρόκειται για ειδική περίπτωση του θεωρήματος Carnot στο συννημένο της προηγούμενης ανάρτησης).
για τα οποία είναι γνωστό πως υπάρχει κωνική που περνά από τις κορυφές τους (πρόκειται για ειδική περίπτωση του θεωρήματος Carnot στο συννημένο της προηγούμενης ανάρτησης). .Άρα οι 2 ενελίξεις ταυτίζονται και συνεπώς για οποιοδήποτε σημείο
.Άρα οι 2 ενελίξεις ταυτίζονται και συνεπώς για οποιοδήποτε σημείο  και το θεώρημα ουσιαστικά δείχτηκε.
και το θεώρημα ουσιαστικά δείχτηκε. έχει 4 ρίζες άρα η παράγωγος αυτής θα έχει 3 ρίζες. Δηλ. η
έχει 4 ρίζες άρα η παράγωγος αυτής θα έχει 3 ρίζες. Δηλ. η  θα έχει τρεις ρίζες και επειδή είναι 3ου βαθμού θα έχει την μορφή του σχήματος (μπλέ καμπύλη).
θα έχει τρεις ρίζες και επειδή είναι 3ου βαθμού θα έχει την μορφή του σχήματος (μπλέ καμπύλη). έχει το πολύ 2 ρίζες άρα η παράγωγος αυτής έχει μία ακριβώς ρίζα, δηλ.
έχει το πολύ 2 ρίζες άρα η παράγωγος αυτής έχει μία ακριβώς ρίζα, δηλ.  . Είναι η μπλέ καμπύλη μετατοπισμένη προς τα πάνω κατά
. Είναι η μπλέ καμπύλη μετατοπισμένη προς τα πάνω κατά  (πράσινη) έτσι ώστε τα τοπικά ακρότατα να βρίσκονται πάνω από τον άξονα
(πράσινη) έτσι ώστε τα τοπικά ακρότατα να βρίσκονται πάνω από τον άξονα  .
. βρίσκεται μετατοπισμένη προς τα πάνω κατά
βρίσκεται μετατοπισμένη προς τα πάνω κατά  , άρα η
, άρα η  έχει επίσης μία ακριβώς ρίζα δηλ. η παράγουσα αυτής η
έχει επίσης μία ακριβώς ρίζα δηλ. η παράγουσα αυτής η 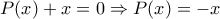 θα έχει το πολύ
θα έχει το πολύ  ρίζες.
ρίζες.