Β΄ Παγκύπριος Διαγωνισμός Επιλογής για JBMO, 2019
Δημοσιεύτηκε: Κυρ Φεβ 10, 2019 1:48 pm
Πρόβλημα 1
Έστω πρώτος αριθμός και
πρώτος αριθμός και  ακέραιος αριθμός, τέτοιοι ώστε να ισχύουν:
ακέραιος αριθμός, τέτοιοι ώστε να ισχύουν:
 Ο αριθμός
Ο αριθμός  είναι πολλαπλάσιο του
είναι πολλαπλάσιο του  .
.
 Ο αριθμός
Ο αριθμός  είναι πολλαπλάσιο του
είναι πολλαπλάσιο του 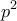 .
.
 Ο αριθμός
Ο αριθμός 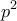 δεν διαιρεί τον
δεν διαιρεί τον  .
.
Να αποδείξετε ότι ο αριθμός είναι πολλαπλάσιο του
είναι πολλαπλάσιο του  .
.
Πρόβλημα 2
Έστω θετικοί ακέραιοι , ώστε ο αριθμός
, ώστε ο αριθμός  να είναι επίσης θετικός ακέραιος.
να είναι επίσης θετικός ακέραιος.
(α) Να αποδείξετε ότι
(β) Να βρείτε την ελάχιστη δυνατή τιμή της παράστασης .
.
Πρόβλημα 3
Δίνεται ισοσκελές τρίγωνο με
με  και
και  . Ονομάζουμε
. Ονομάζουμε  το σημείο τομής της μεσοκαθέτου του
το σημείο τομής της μεσοκαθέτου του  και της εσωτερικής διχοτόμου της γωνίας
και της εσωτερικής διχοτόμου της γωνίας 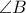 του τριγώνου
του τριγώνου  . Ο κύκλος με διάμετρο το
. Ο κύκλος με διάμετρο το  τέμνει την ευθεία
τέμνει την ευθεία  στο σημείο
στο σημείο  . Αν η εφαπτομένη του κύκλου στο
. Αν η εφαπτομένη του κύκλου στο  τέμνει την
τέμνει την  στο σημείο
στο σημείο  , να αποδείξετε ότι
, να αποδείξετε ότι  .
.
Πρόβλημα 4
Σε μια συνάντηση ατόμων, κάθε άτομο αντιπαθεί ακριβώς ένα άλλο άτομο. (Η αντιπάθεια δεν είναι απαραίτητα αμοιβαία.)
ατόμων, κάθε άτομο αντιπαθεί ακριβώς ένα άλλο άτομο. (Η αντιπάθεια δεν είναι απαραίτητα αμοιβαία.)
(α) Να αποδείξετε ότι μπορούμε να επιλέξουμε άτομα, ώστε καθένα από αυτά να μην αντιπαθεί κάποιο άλλο άτομο από αυτά.
άτομα, ώστε καθένα από αυτά να μην αντιπαθεί κάποιο άλλο άτομο από αυτά.
(β) Να βρείτε παράδειγμα για το οποίο όπως και να επιλέξουμε άτομα, κάποιο από αυτά θα αντιπαθεί κάποιο άλλο από αυτά.
άτομα, κάποιο από αυτά θα αντιπαθεί κάποιο άλλο από αυτά.
Έστω
 πρώτος αριθμός και
πρώτος αριθμός και  ακέραιος αριθμός, τέτοιοι ώστε να ισχύουν:
ακέραιος αριθμός, τέτοιοι ώστε να ισχύουν:  Ο αριθμός
Ο αριθμός  είναι πολλαπλάσιο του
είναι πολλαπλάσιο του  .
. Ο αριθμός
Ο αριθμός  είναι πολλαπλάσιο του
είναι πολλαπλάσιο του 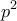 .
. Ο αριθμός
Ο αριθμός 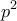 δεν διαιρεί τον
δεν διαιρεί τον  .
.Να αποδείξετε ότι ο αριθμός
 είναι πολλαπλάσιο του
είναι πολλαπλάσιο του  .
.Πρόβλημα 2
Έστω θετικοί ακέραιοι
 , ώστε ο αριθμός
, ώστε ο αριθμός  να είναι επίσης θετικός ακέραιος.
να είναι επίσης θετικός ακέραιος.(α) Να αποδείξετε ότι

(β) Να βρείτε την ελάχιστη δυνατή τιμή της παράστασης
 .
.Πρόβλημα 3
Δίνεται ισοσκελές τρίγωνο
 με
με  και
και  . Ονομάζουμε
. Ονομάζουμε  το σημείο τομής της μεσοκαθέτου του
το σημείο τομής της μεσοκαθέτου του  και της εσωτερικής διχοτόμου της γωνίας
και της εσωτερικής διχοτόμου της γωνίας 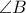 του τριγώνου
του τριγώνου  . Ο κύκλος με διάμετρο το
. Ο κύκλος με διάμετρο το  τέμνει την ευθεία
τέμνει την ευθεία  στο σημείο
στο σημείο  . Αν η εφαπτομένη του κύκλου στο
. Αν η εφαπτομένη του κύκλου στο  τέμνει την
τέμνει την  στο σημείο
στο σημείο  , να αποδείξετε ότι
, να αποδείξετε ότι  .
. Πρόβλημα 4
Σε μια συνάντηση
 ατόμων, κάθε άτομο αντιπαθεί ακριβώς ένα άλλο άτομο. (Η αντιπάθεια δεν είναι απαραίτητα αμοιβαία.)
ατόμων, κάθε άτομο αντιπαθεί ακριβώς ένα άλλο άτομο. (Η αντιπάθεια δεν είναι απαραίτητα αμοιβαία.)(α) Να αποδείξετε ότι μπορούμε να επιλέξουμε
 άτομα, ώστε καθένα από αυτά να μην αντιπαθεί κάποιο άλλο άτομο από αυτά.
άτομα, ώστε καθένα από αυτά να μην αντιπαθεί κάποιο άλλο άτομο από αυτά.(β) Να βρείτε παράδειγμα για το οποίο όπως και να επιλέξουμε
 άτομα, κάποιο από αυτά θα αντιπαθεί κάποιο άλλο από αυτά.
άτομα, κάποιο από αυτά θα αντιπαθεί κάποιο άλλο από αυτά. και η διχοτόμος της
και η διχοτόμος της  τέμνονται στον περίκυκλο του
τέμνονται στον περίκυκλο του  άρα το
άρα το  είναι εγγράψιμο και
είναι εγγράψιμο και  Επειδή
Επειδή 





 που ισχύει αφού
που ισχύει αφού 

 που ισχύει αφού
που ισχύει αφού 
 , και
, και  , άρα
, άρα  .
. , οπότε
, οπότε  .
. , και θέλουμε
, και θέλουμε  , που είναι προφανές (
, που είναι προφανές ( ).
). και θέλουμε
και θέλουμε  , που είναι πάλι προφανές.
, που είναι πάλι προφανές. .
. είναι 1, WLOG
είναι 1, WLOG  . Τότε,
. Τότε,  , και πρέπει
, και πρέπει  .
. με παράγωγο
με παράγωγο  , είναι γνησίως αύξουσα, άρα
, είναι γνησίως αύξουσα, άρα  .
. είναι
είναι  .
. , με όμοια σκέψη βρίσκω ελάχιστη τιμή ίση με 10, για
, με όμοια σκέψη βρίσκω ελάχιστη τιμή ίση με 10, για 
 , WLOG
, WLOG  με
με  και
και  .
.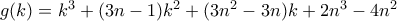 , και αφού όλοι οι συντελεστές είναι θετικοί
, και αφού όλοι οι συντελεστές είναι θετικοί ) η
) η  είναι γνησίως αύξουσα, άρα
είναι γνησίως αύξουσα, άρα  .
. , και λαμβάνεται όταν
, και λαμβάνεται όταν 
 , τα άτομα.
, τα άτομα. αυτά άτομα σε σύνολα των
αυτά άτομα σε σύνολα των  , ώστε σε κάθε σύνολο, για κάθε δύο άτομα ο ένας να αντιπαθεί τον άλλο (υπάρχει και ένα σύνολο που αποτελείται από μόνο ένα άτομο!)
, ώστε σε κάθε σύνολο, για κάθε δύο άτομα ο ένας να αντιπαθεί τον άλλο (υπάρχει και ένα σύνολο που αποτελείται από μόνο ένα άτομο!)


 .
.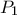 αντιπαθεί τον
αντιπαθεί τον  και ο
και ο  , στο δεύτερο ο
, στο δεύτερο ο  τον
τον  κλπ.
κλπ. .
. δεν αντιπαθεί κανένα εκ των
δεν αντιπαθεί κανένα εκ των  , είμαστε εντάξει.
, είμαστε εντάξει. .
. να αντιπαθεί τον
να αντιπαθεί τον  , για κάθε
, για κάθε  .
. άτομα) τουλάχιστον δύο από αυτά θ'ανήκουν σε ένα από τα σύνολα
άτομα) τουλάχιστον δύο από αυτά θ'ανήκουν σε ένα από τα σύνολα  .
. και έχουμε τις εξής αντιπάθειες:
και έχουμε τις εξής αντιπάθειες: , ο
, ο  αντιπαθεί τον
αντιπαθεί τον  , αυτός τον
, αυτός τον  , αυτός τον
, αυτός τον  και αυτός τον
και αυτός τον 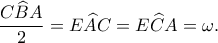 Είναι ακόμα,
Είναι ακόμα,  με
με 

