Σελίδα 1 από 3
IMO 2018
Δημοσιεύτηκε: Δευ Ιούλ 09, 2018 11:04 am
από Διονύσιος Αδαμόπουλος
Καλή Επιτυχία στις ομάδες της Ελλάδας και της Κύπρου στη Διεθνή Μαθηματική Ολυμπιάδα, όπου σήμερα είναι η πρώτη διαγωνιστική μέρα

.
Εδώ είναι η επίσημη Ιστοσελίδα
Re: IMO 2018
Δημοσιεύτηκε: Δευ Ιούλ 09, 2018 11:52 am
από Ορέστης Λιγνός
Καλή επιτυχία στην Ελληνική και στην Κυπριακή αποστολή!
Re: IMO 2018
Δημοσιεύτηκε: Δευ Ιούλ 09, 2018 1:40 pm
από S.E.Louridas
Εύχομαι από καρδιάς καλή επιτυχία στους Έλληνες διαγωνιζόμενους, αλλά και στους Κύπριους αδελφούς μας διαγωνιζόμενους.
Καλή επάνοδο στην Ελλάδα μας και στην Κύπρο.
Re: IMO 2018
Δημοσιεύτηκε: Δευ Ιούλ 09, 2018 1:43 pm
από Τσιαλας Νικολαος
Καλή επιτυχία σε όλα τα παιδιά της Ελλάδος και της Κύπρου και ιδιαίτερα στους 2 Δημητράκηδες!!!
Re: IMO 2018
Δημοσιεύτηκε: Δευ Ιούλ 09, 2018 2:25 pm
από Demetres
Πρόβλημα 1
Έστω οξυγώνιο τρίγωνο

και έστω

ο περιγεγραμμένος κύκλος του. Τα σημεία

και

βρίσκονται στα τμήματα

και

αντίστοιχα ώστε

. Οι μεσοκάθετες των

και

τέμνουν τα μικρά τόξα

και

του

στα σημεία

και

αντίστοιχα. Να αποδειχθεί ότι οι ευθείες

και

είτε είναι παράλληλες είτε είναι οι ταυτόσημες.
Πρόβλημα 2
Να βρεθούν όλοι οι ακέραιοι

για τους οποίους υπάρχουν πραγματικοί αριθμοί

οι οποίοι ικανοποιούν

,

και

για

.
Πρόβλημα 3
Ένα τρίγωνο αντι-Πασκάλ είναι μια τριγωνική διάταξη αριθμών έτσι ώστε εκτός από τους αριθμούς της τελευταίας σειράς, κάθε αριθμός είναι η απόλυτη τιμή της διαφοράς των δύο αριθμών που βρίσκονται αμέσως από κάτω του. Π.χ. το πιο κάτω είναι ένα τρίγωνο αντι-Πασκάλ με τέσσερις σειρές που περιέχει κάθε αριθμό από το

ως το

.

Υπάρχει τρίγωνο αντι-Πασκάλ με

σειρές το οποίο να περιέχει κάθε ακέραιο από το

ως το

;
Πρόβλημα 4
Ένα
κελί, είναι ένα σημείο

του επιπέδου ώστε τα

και

να είναι και τα δύο θετικοί ακέραιοι μικρότεροι ή ίσοι του

.
Αρχικά υπάρχουν
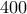
κενά κελιά. Ο Αντρέας και ο Βασίλης τοποθετούν εναλλάξ πέτρες στα κελιά με τον Αντρέα να αρχίζει πρώτος. Σε κάθε του κίνηση, ο Αντρέας τοποθετεί μια κόκκινη πέτρα σε ένα κενό κελί με τέτοιο τρόπο ώστε κάθε δυο κελιά με κόκκινες πέτρες να μην έχουν απόσταση ίση με

. Σε κάθε του κίνηση, ο Βασίλης τοποθετεί μια μπλε πέτρα σε ένα κενό κελί. (Ο Βασίλης επιτρέπεται να τοποθετήσει πέτρα σε οποιαδήποτε απόσταση από άλλη πέτρα θέλει.) Σταματούν όταν ένας εκ των δύο δεν μπορεί να τοποθετήσει άλλη πέτρα.
Να βρεθεί το μέγιστο

ώστε ο Αντρέας να μπορεί σίγουρα να τοποθετήσει

κόκκινες πέτρες, άσχετα με το πως τοποθετεί τις πέτρες του ο Βασίλης.
Πρόβλημα 5
Δίνεται μια άπειρη ακολουθία

θετικών ακεραίων. Έστω ότι υπάρχει ακέραιος

ώστε για κάθε

, ο αριθμός

να είναι ακέραιος. Να δειχθεί ότι υπάρχει θετικός ακέραιος

έτσι ώστε

για κάθε

.
Πρόβλημα 6
Ένα κυρτό τετράπλευρο

ικανοποιεί

=

. Σημείο

στο εσωτερικό του

είναι τέτοιο ώστε

και

.
Να δειχθεί ότι

.
Re: IMO 2018
Δημοσιεύτηκε: Δευ Ιούλ 09, 2018 3:52 pm
από Ορέστης Λιγνός
Demetres έγραψε: ↑Δευ Ιούλ 09, 2018 2:25 pm
Πρόβλημα 1
Έστω οξυγώνιο τρίγωνο

και έστω

ο περιγεγραμμένος κύκλος του. Τα σημεία

και

βρίσκονται στα τμήματα

και

αντίστοιχα ώστε

. Οι μεσοκάθετες των

και

τέμνουν τα μικρά τόξα

και

του

στα σημεία

και

αντίστοιχα. Να αποδειχθεί ότι οι ευθείες

και

είτε είναι παράλληλες είτε είναι οι ταυτόσημες.
Έστω ότι οι δύο μεσοκάθετοι τέμνονται στο

και

. Έστω

το έκκεντρο του τριγώνου

. Τότε, προφανώς έχουμε

. Έστω

. Τότε, το

είναι εγγράψιμο, οπότε

, και όμοια

. Άρα, αν

, έχουμε

, ό.έ.δ.
(Προφανώς, όταν
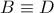
, οι ευθείες ταυτίζονται).
Re: IMO 2018
Δημοσιεύτηκε: Δευ Ιούλ 09, 2018 3:57 pm
από Ορέστης Λιγνός
Demetres έγραψε: ↑Δευ Ιούλ 09, 2018 2:25 pm
Πρόβλημα 2
Να βρεθούν όλοι οι ακέραιοι

για τους οποίους υπάρχουν πραγματικοί αριθμοί

οι οποίοι ικανοποιούν

,

και

για

.
Έχουμε

άρα
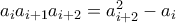
για κάθε

.
Άρα,

Επίσης,
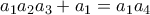
etc, so

, όπου

. Από AM-GM,

και εφαρμόζοντας την, έχουμε ισότητα, άρα

.
Αν τώρα

δεν είναι

, έχουμε δύο περιπτώσεις. Αν

:

άρα τελικά όλα τα

είναι ίσα, οπότε

, άτοπο.
Όμοια,

είναι άτοπο, άρα

, και μπορούμε εύκολα να κάνουμε μία κατασκευή, π.χ.


φορές.
Άρα η

είναι η μόνη λύση στο πρόβλημα.
Re: IMO 2018
Δημοσιεύτηκε: Δευ Ιούλ 09, 2018 4:08 pm
από Demetres
Demetres έγραψε: ↑Δευ Ιούλ 09, 2018 2:25 pm
Πρόβλημα 2
Να βρεθούν όλοι οι ακέραιοι

για τους οποίους υπάρχουν πραγματικοί αριθμοί

οι οποίοι ικανοποιούν

,

και

για

.
Ωραίο!
Για

πολλαπλάσιο του

γίνεται αν πάρουμε την ακολουθία

. Ας υποθέσουμε λοιπόν ότι

.
Παρατηρούμε ότι

για κάθε

. (Όπου

.)
Άρα

Από την ανισότητα της αναδιάταξης είναι

για κάθε

. Επειδή

, παίρνουμε

. Έστω

. Τότε

. Αλλά

, άτοπο.
Ισχύει λοιπόν αν και μόνο αν

.

Δεν πρόσεξα ότι απάντησε ο Ορέστης με ουσιαστικά την ίδια λύση.
Re: IMO 2018
Δημοσιεύτηκε: Δευ Ιούλ 09, 2018 5:29 pm
από Διονύσιος Αδαμόπουλος
Demetres έγραψε: ↑Δευ Ιούλ 09, 2018 2:25 pm
Πρόβλημα 1
Έστω οξυγώνιο τρίγωνο

και έστω

ο περιγεγραμμένος κύκλος του. Τα σημεία

και

βρίσκονται στα τμήματα

και

αντίστοιχα ώστε

. Οι μεσοκάθετες των

και

τέμνουν τα μικρά τόξα

και

του

στα σημεία

και

αντίστοιχα. Να αποδειχθεί ότι οι ευθείες

και

είτε είναι παράλληλες είτε είναι οι ταυτόσημες.
Μια διαφορετική λύση από αυτή του Ορέστη, η οποία είναι λίγο πιο "άκομψη".
Δεν αναλύω τις τετριμμένες περιπτώσεις που ένα από τα
ταυτίζεται με τα

αντίστοιχα.

- IMO 2018 P1.png (34 KiB) Προβλήθηκε 6704 φορές
Έστω πως η

τέμνει τον περιγεγραμμένο κύκλο του

σε σημείο

.
Παρατηρούμε πως

.
Άρα το τρίγωνο

είναι ισοσκελές, με

.
Όμοια αν η

τέμνει τον περιγεγραμμένο κύκλο του

στο

, τότε

.
Θα αποδείξουμε πως

, δηλαδή

.
Παρατηρούμε πως

, ενώ

(αφού η

είναι επίκεντρη της

στο κύκλο με κέντρο

και ακτίνα

.
Άρα αρκεί να αποδείξουμε πως

, δηλαδή

.
Ξέρουμε όμως πως

, από τον ορισμό του

.
Άρα αρκεί

.
Παρατηρούμε πως το τετράπλευρο

είναι εγγράψιμο και

, άρα η

είναι η διχοτόμος της
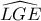
.
Αν το

δεν ήταν ισοσκελές, τότε αφού το

ανήκει στη διχοτόμο της
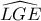
και

, θα έπρεπε το

να είναι εγγράψιμο (θεώρημα νότιου πόλου), άτοπο, αφού ο περιγεγραμμένος κύκλος του

είναι ο περιγεγραμμένος κύκλος του

και το

δεν ανήκει σε αυτό το κύκλο.
Άρα το

είναι ισοσκελές με

και το ζητούμενο έπεται.
EDIT: Προστέθηκε το σχήμα!
Re: IMO 2018
Δημοσιεύτηκε: Δευ Ιούλ 09, 2018 7:02 pm
από Datis-Kalali
Demetres έγραψε: ↑Δευ Ιούλ 09, 2018 2:25 pm
Πρόβλημα 1
Έστω οξυγώνιο τρίγωνο

και έστω

ο περιγεγραμμένος κύκλος του. Τα σημεία

και

βρίσκονται στα τμήματα

και

αντίστοιχα ώστε

. Οι μεσοκάθετες των

και

τέμνουν τα μικρά τόξα

και

του

στα σημεία

και

αντίστοιχα. Να αποδειχθεί ότι οι ευθείες

και

είτε είναι παράλληλες είτε είναι οι ταυτόσημες.
Θα χρησιμοπουμε μιγαδικοί αριθμοί
Έστω ότι Γ είανι το μοναδιαίο κύκλο και έστω ότι

,

είναι το σημείο τομής των

και

με των μεσοκάθετων τους αντίστοιχα.
Τωρά

και

![d=2h_1-b=2\left[\frac12\left(a+b+f-\frac{ab}{f}\right)\right] - b = a+f-\frac{ab}{f} d=2h_1-b=2\left[\frac12\left(a+b+f-\frac{ab}{f}\right)\right] - b = a+f-\frac{ab}{f}](/forum/ext/geomar/texintegr/latexrender/pictures/083a626a43191a28c9cc252e81fa7c0a.png)
και

Επίσης




Έχουμε 2 περιπτώσεις
Περίπτωση 1:

Εδώ

και
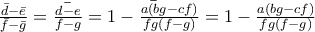
αφού

Άρα οι ευθείες

και

είτε είναι παράλληλες είτε είναι οι ταυτόσημες.
Περίπτωση 2:


Αλλά

και

(είναι φανερό)
Οπότε

ειναι πάνω στα τόξα

και

δηλαδή είανι τα ίσα κλάσματα είανι το σημείο Α
Δηλαδή

που είανι ακριβώς η περίπτωση 1.
Άρα η απόδειξη ολοκληρώθηκε.

Re: IMO 2018
Δημοσιεύτηκε: Δευ Ιούλ 09, 2018 7:52 pm
από Ορέστης Λιγνός
Demetres έγραψε: ↑Δευ Ιούλ 09, 2018 2:25 pm
Πρόβλημα 3
Ένα τρίγωνο αντι-Πασκάλ είναι μια τριγωνική διάταξη αριθμών έτσι ώστε εκτός από τους αριθμούς της τελευταίας σειράς, κάθε αριθμός είναι η απόλυτη τιμή της διαφοράς των δύο αριθμών που βρίσκονται αμέσως από κάτω του. Π.χ. το πιο κάτω είναι ένα τρίγωνο αντι-Πασκάλ με τέσσερις σειρές που περιέχει κάθε αριθμό από το

ως το

.

Υπάρχει τρίγωνο αντι-Πασκάλ με

σειρές το οποίο να περιέχει κάθε ακέραιο από το

ως το

;
Με παίδεψε πολύ αυτή η άσκηση ...
Καταρχήν, θα ''γυρίσω'' ανάποδα το τρίγωνο (έτσι ώστε στην βάση του να υπάρχει μόνο

αριθμός)
Λοιπόν, ξεκινάμε ορίζοντας:
Base: ο αριθμός στην βάση του τριγώνου.
Τώρα, σχηματίζουμε μία γραμμή, ξεκινώντας από τον base, έχουμε τους δύο αποπάνω αριθμούς, από τους οποίους σχηματίστηκε ο base, και από αυτούς παίρνουμε τον μεγαλύτερο, και κάνουμε την ίδια διαδικασία. Όλοι αυτοί οι αριθμοί, οι ''μεγάλοι'' σχηματίζουν μία γραμμή, που την ονομάζουμε
big line. Οι ''μικρότεροι'' αριθμοί, ονομάζονται
small numbers.
Ο μεγαλύτερος αριθμός στην πάνω σειρά, ονομάζεται
big.
Από τον big, φέρνουμε παράλληλη προς μία πλευρά του τριγώνου, όπως και από τον αριθμό δεξιά από τον big, και σχηματίζουμε δύο σχήματα, που έχουν τις ιδιότητες τις εκφώνησης για το αντί-Πασκάλ (εκτός από ότι περιέχει κάθε ακέραιο). Αυτά τα ονομάζουμε sub-triangles.
Π.χ. για

έχουμε το :

- IMO 2018 Problem 3.png (14.17 KiB) Προβλήθηκε 6954 φορές
όπου η γραμμή είναι η big line, οι μαύροι αριθμοί αποτελούν τα subtriangles, οι κυκλωμένοι αριθμοί είναι οι small numbers και o

είναι ο base.
Επίσης, εύκολα αποδεικνύεται ότι ο big είναι ίσος με το άθροισμα των small numbers και του base. Οπό
Οπότε μετράμε το ελάχιστο άθροισμα των base και των small numbers στα sub-triangles, που είναι

.
Επίσης, αφού έχουμε δύο subtriangles, το άθροισμα των big τους είναι το πολύ

, άρα

, οπότε καταλήγουμε ότι αν

, άρα και για

είναι αδύνατο να κατασκευαστεί ένα αντι-Πασκάλ.
Re: IMO 2018
Δημοσιεύτηκε: Δευ Ιούλ 09, 2018 8:38 pm
από S.E.Louridas
Demetres έγραψε: ↑Δευ Ιούλ 09, 2018 2:25 pm
Πρόβλημα 1
Έστω οξυγώνιο τρίγωνο

και έστω

ο περιγεγραμμένος κύκλος του. Τα σημεία

και

βρίσκονται στα τμήματα

και

αντίστοιχα ώστε

. Οι μεσοκάθετες των

και

τέμνουν τα μικρά τόξα

και

του

στα σημεία

και

αντίστοιχα. Να αποδειχθεί ότι οι ευθείες

και

είτε είναι παράλληλες είτε είναι οι ταυτόσημες.
Εντάξει είναι ένα καλό πρόβλημα, ιδανικό για πρώτο θέμα, ας πούμε για «προθέρμανση» (πιστεύω ότι στο πρόβλημα αυτό οι Έλληνες διαγωνιζόμενοι θα "κτυπήσουν" όλοι άριστα). Για να δούμε και την αυριανή μέρα αν θα έχει και κάποιο πιό στιβαρό γεωμετρικό θέμα, για Ολυμπιάδα ... ίδωμεν. Και το λέω αυτό γιατί αργά αλλά σταθερά, έχουμε αλλαγή νοοτροποίας στην θεματολογία των διεθνών διαγωνισμών, με την ελπίδα οι σύγχρονοι τροπαιούχοι να έχουν την ίδια δυνατότητα να κατανοούν αργότερα έννοιες από την πραγματική ανάλυση, την διαφορική γεωμετρία την τοπολογία, την άλγεβρα κτλ., άν αυτό βέβαια παραμένει ζητούμενο. .... και πάλι ίδωμεν ... αφού ένας ισυχρός σύμμαχος της αλήθειας είναι ο χρόνος.
Απλά ας δούμε τώρα για το πρόβλημα αυτό και μία «αιρετική» λύση, κύρια για λόγους πλουραλισμού:
Στο σχήμα θεωρούμε

Άμεσα παρατηρούμε ότι

Τα Τρίγωνα

και

είναι αμβλυγώνια και ίσα, αφού έχουμε

.
Επομένως

Συνεπώς

Όταν το σημείο

συμπέσει με το σημείο

, τότε έχουμε ταύτιση των ευθειών


- ιμο.png (13.06 KiB) Προβλήθηκε 6864 φορές
Re: IMO 2018
Δημοσιεύτηκε: Τρί Ιούλ 10, 2018 2:34 pm
από Demetres
Άρχισα να ανεβάζω και τα προβλήματα της δεύτερης μέρας στην αρχική μου ανάρτηση.
Re: IMO 2018
Δημοσιεύτηκε: Τρί Ιούλ 10, 2018 3:06 pm
από Datis-Kalali
Demetres έγραψε: ↑Δευ Ιούλ 09, 2018 2:25 pm
Πρόβλημα 4
Ένα
κελί, είναι ένα σημείο

του επιπέδου ώστε τα

και

να είναι και τα δύο θετικοί ακέραιοι μικρότεροι ή ίσοι του

.
Αρχικά υπάρχουν
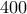
κενά κελιά. Ο Αντρέας και ο Βασίλης τοποθετούν εναλλάξ πέτρες στα κελιά με τον Αντρέα να αρχίζει πρώτος. Σε κάθε του κίνηση, ο Αντρέας τοποθετεί μια κόκκινη πέτρα σε ένα κενό κελί με τέτοιο τρόπο ώστε κάθε δυο κελιά με κόκκινες πέτρες να μην έχουν απόσταση ίση με

. Σε κάθε του κίνηση, ο Βασίλης τοποθετεί μια μπλε πέτρα σε ένα κενό κελί. (Ο Βασίλης επιτρέπεται να τοποθετήσει πέτρα σε οποιαδήποτε απόσταση από άλλη πέτρα θέλει.) Σταματούν όταν ένας εκ των δύο δεν μπορεί να τοποθετήσει άλλη πέτρα.
Να βρεθεί το μέγιστο

ώστε ο Αντρέας να μπορεί σίγουρα να τοποθετήσει

κόκκινες πέτρες, άσχετα με το πως τοποθετεί τις πέτρες του ο Βασίλης.
Θεωρούμε το καρτεσιανό σύστημα αναφοράς στον επίπεδο μας. Δύο σημεία που απέχονται

πρέπει να απέχονται 2 σημεία στον άξονα χ και 1 σημείο στον άξονα ψ, η αντίστροφο. Έτσι εαν ενώσουμε όλα τα σημεία που απέχονται

έχουμε ένα γράφημα με 100 κύκλους (κάθε κύκλο περιέχει 4 κορυφές). Τωρά ο Βασιλής για να παίζει το καλύτερο του μπορεί να βάλει ένα μπλέ πέτρα στον κύκλο (που έβαλε προηγουμένως μια κόκκινη πετρα) έτσι ώστε ο Αντρέας να μην μπορεί να τοποθετεί άλλη πέτρα σε αυτο το κύκλο. Άρα ο Αντρέας μπορεί να τοποθετεί το πολύ 100 πέτρα. Αλλά εαν χρωματίζουμε τα σημεία μαυρό και άσπρο εναλλάξ, έχουμε 200 άσπρα σημεία μισά απο το οποία μπορεί να βάλει πέτρα ο Αντρέας κόκκινα πέτρα, έστι ώστε να μην απέχονται

. Άρα

Re: IMO 2018
Δημοσιεύτηκε: Τρί Ιούλ 10, 2018 4:31 pm
από Datis-Kalali
Demetres έγραψε: ↑Δευ Ιούλ 09, 2018 2:25 pm
Πρόβλημα 5
Δίνεται μια άπειρη ακολουθία

θετικών ακεραίων. Έστω ότι υπάρχει ακέραιος

ώστε για κάθε

, ο αριθμός

να είναι ακέραιος. Να δειχθεί ότι υπάρχει θετικός ακέραιος

έτσι ώστε

για κάθε

.
Έστω ότι

Καταρχάς
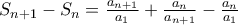
είναι ακέραιος.
Οπότε

Έφτασα μεχρί εδώ και δεν ξέρω πως να προχωρίσω
Re: IMO 2018
Δημοσιεύτηκε: Τρί Ιούλ 10, 2018 5:18 pm
από Demetres
Demetres έγραψε: ↑Δευ Ιούλ 09, 2018 2:25 pm
Πρόβλημα 5
Δίνεται μια άπειρη ακολουθία

θετικών ακεραίων. Έστω ότι υπάρχει ακέραιος

ώστε για κάθε

, ο αριθμός

να είναι ακέραιος. Να δειχθεί ότι υπάρχει θετικός ακέραιος

έτσι ώστε

για κάθε

.
Ωραία και αυτό.
Γράφω

για τον μέγιστο κοινό διαιρέτη των

και

. Θα δείξω αρχικά ότι

.
Αν δεν ισχύει αυτό τότε θα υπάρχει πρώτος

ώστε

και

Γνωρίζουμε ότι ο

είναι ακέραιος για

.
Αν κάνουμε ανάγωγο το πρώτο κλάσμα, ο παρονομαστής του δεν θα είναι πολλαπλάσιο του

. Στο δεύτερο όμως κλάσμα θα είναι. Αυτό είναι άτοπο και άρα ο ισχυρισμός μας αποδείχθηκε.
Επειδή κάθε

είναι μικρότερο ή ίσο από το

, τότε θα υπάρχει

ώστε

για κάθε

.
Έστω ότι όλα τα

είναι ίσα με

για

. Γράφουμε

και

για

. Τότε

για κάθε

. Θα έχουμε επίσης ότι το

είναι ακέραιος.
Κάνοντας ομώνυμα βρίσκουμε ότι

και επειδή

, τότε

.
Αφού

για κάθε

θα υπάρχει και

ώστε

για κάθε

. Αλλά τότε είναι και

για κάθε

.
Re: IMO 2018
Δημοσιεύτηκε: Τετ Ιούλ 11, 2018 12:12 pm
από silouan
Demetres έγραψε: ↑Δευ Ιούλ 09, 2018 2:25 pm
Πρόβλημα 1
Έστω οξυγώνιο τρίγωνο

και έστω

ο περιγεγραμμένος κύκλος του. Τα σημεία

και

βρίσκονται στα τμήματα

και

αντίστοιχα ώστε

. Οι μεσοκάθετες των

και

τέμνουν τα μικρά τόξα

και

του

στα σημεία

και

αντίστοιχα. Να αποδειχθεί ότι οι ευθείες

και

είτε είναι παράλληλες είτε είναι οι ταυτόσημες.
Το πρόβλημα αυτό προτάθηκε από την Ελλάδα από τους: Βαγγέλη Ψύχα, Μιχάλη Σαράντη και τον υπογράφοντα

Re: IMO 2018
Δημοσιεύτηκε: Τετ Ιούλ 11, 2018 12:36 pm
από nikolaos p.
Καλή επιτυχία!

Re: IMO 2018
Δημοσιεύτηκε: Τετ Ιούλ 11, 2018 12:38 pm
από Τσιαλας Νικολαος
silouan έγραψε: ↑Τετ Ιούλ 11, 2018 12:12 pm
Demetres έγραψε: ↑Δευ Ιούλ 09, 2018 2:25 pm
Πρόβλημα 1
Έστω οξυγώνιο τρίγωνο

και έστω

ο περιγεγραμμένος κύκλος του. Τα σημεία

και

βρίσκονται στα τμήματα

και

αντίστοιχα ώστε

. Οι μεσοκάθετες των

και

τέμνουν τα μικρά τόξα

και

του

στα σημεία

και

αντίστοιχα. Να αποδειχθεί ότι οι ευθείες

και

είτε είναι παράλληλες είτε είναι οι ταυτόσημες.
Το πρόβλημα αυτό προτάθηκε από την Ελλάδα από τους: Βαγγέλη Ψύχα, Μιχάλη Σαράντη και τον υπογράφοντα

Συγχαρητήρια και στους 3!! Κανά νέο για τα αποτελέσματα των αποστολών μας έχουμε Σιλουανέ?
Re: IMO 2018
Δημοσιεύτηκε: Τετ Ιούλ 11, 2018 2:23 pm
από Σταύρος Σταυρόπουλος
silouan έγραψε: ↑Τετ Ιούλ 11, 2018 12:12 pm
Demetres έγραψε: ↑Δευ Ιούλ 09, 2018 2:25 pm
Πρόβλημα 1
Έστω οξυγώνιο τρίγωνο

και έστω

ο περιγεγραμμένος κύκλος του. Τα σημεία

και

βρίσκονται στα τμήματα

και

αντίστοιχα ώστε

. Οι μεσοκάθετες των

και

τέμνουν τα μικρά τόξα

και

του

στα σημεία

και

αντίστοιχα. Να αποδειχθεί ότι οι ευθείες

και

είτε είναι παράλληλες είτε είναι οι ταυτόσημες.
Το πρόβλημα αυτό προτάθηκε από την Ελλάδα από τους: Βαγγέλη Ψύχα, Μιχάλη Σαράντη και τον υπογράφοντα

ΘΕΡΜΑ ΣΥΓΧΑΡΗΤΗΡΙΑ!!!!
 .
. και έστω
και έστω  ο περιγεγραμμένος κύκλος του. Τα σημεία
ο περιγεγραμμένος κύκλος του. Τα σημεία  και
και  βρίσκονται στα τμήματα
βρίσκονται στα τμήματα  και
και  αντίστοιχα ώστε
αντίστοιχα ώστε  . Οι μεσοκάθετες των
. Οι μεσοκάθετες των  και
και  τέμνουν τα μικρά τόξα
τέμνουν τα μικρά τόξα  και
και  αντίστοιχα. Να αποδειχθεί ότι οι ευθείες
αντίστοιχα. Να αποδειχθεί ότι οι ευθείες  και
και  είτε είναι παράλληλες είτε είναι οι ταυτόσημες.
είτε είναι παράλληλες είτε είναι οι ταυτόσημες. για τους οποίους υπάρχουν πραγματικοί αριθμοί
για τους οποίους υπάρχουν πραγματικοί αριθμοί  οι οποίοι ικανοποιούν
οι οποίοι ικανοποιούν  ,
, 
 για
για  .
. ως το
ως το  .
.
 σειρές το οποίο να περιέχει κάθε ακέραιο από το
σειρές το οποίο να περιέχει κάθε ακέραιο από το  ;
; του επιπέδου ώστε τα
του επιπέδου ώστε τα  και
και  να είναι και τα δύο θετικοί ακέραιοι μικρότεροι ή ίσοι του
να είναι και τα δύο θετικοί ακέραιοι μικρότεροι ή ίσοι του  .
.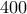 κενά κελιά. Ο Αντρέας και ο Βασίλης τοποθετούν εναλλάξ πέτρες στα κελιά με τον Αντρέα να αρχίζει πρώτος. Σε κάθε του κίνηση, ο Αντρέας τοποθετεί μια κόκκινη πέτρα σε ένα κενό κελί με τέτοιο τρόπο ώστε κάθε δυο κελιά με κόκκινες πέτρες να μην έχουν απόσταση ίση με
κενά κελιά. Ο Αντρέας και ο Βασίλης τοποθετούν εναλλάξ πέτρες στα κελιά με τον Αντρέα να αρχίζει πρώτος. Σε κάθε του κίνηση, ο Αντρέας τοποθετεί μια κόκκινη πέτρα σε ένα κενό κελί με τέτοιο τρόπο ώστε κάθε δυο κελιά με κόκκινες πέτρες να μην έχουν απόσταση ίση με  . Σε κάθε του κίνηση, ο Βασίλης τοποθετεί μια μπλε πέτρα σε ένα κενό κελί. (Ο Βασίλης επιτρέπεται να τοποθετήσει πέτρα σε οποιαδήποτε απόσταση από άλλη πέτρα θέλει.) Σταματούν όταν ένας εκ των δύο δεν μπορεί να τοποθετήσει άλλη πέτρα.
. Σε κάθε του κίνηση, ο Βασίλης τοποθετεί μια μπλε πέτρα σε ένα κενό κελί. (Ο Βασίλης επιτρέπεται να τοποθετήσει πέτρα σε οποιαδήποτε απόσταση από άλλη πέτρα θέλει.) Σταματούν όταν ένας εκ των δύο δεν μπορεί να τοποθετήσει άλλη πέτρα. ώστε ο Αντρέας να μπορεί σίγουρα να τοποθετήσει
ώστε ο Αντρέας να μπορεί σίγουρα να τοποθετήσει  θετικών ακεραίων. Έστω ότι υπάρχει ακέραιος
θετικών ακεραίων. Έστω ότι υπάρχει ακέραιος  ώστε για κάθε
ώστε για κάθε  , ο αριθμός
, ο αριθμός
 έτσι ώστε
έτσι ώστε  για κάθε
για κάθε  .
. ικανοποιεί
ικανοποιεί  =
=  . Σημείο
. Σημείο  στο εσωτερικό του
στο εσωτερικό του  και
και  .
. .
. . Έστω
. Έστω  το έκκεντρο του τριγώνου
το έκκεντρο του τριγώνου  . Έστω
. Έστω  . Τότε, το
. Τότε, το  είναι εγγράψιμο, οπότε
είναι εγγράψιμο, οπότε  , και όμοια
, και όμοια  . Άρα, αν
. Άρα, αν  , έχουμε
, έχουμε  , ό.έ.δ.
, ό.έ.δ.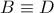 , οι ευθείες ταυτίζονται).
, οι ευθείες ταυτίζονται). άρα
άρα 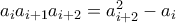 για κάθε
για κάθε  .
. Επίσης,
Επίσης, 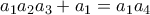 etc, so
etc, so  , όπου
, όπου  . Από AM-GM,
. Από AM-GM,  και εφαρμόζοντας την, έχουμε ισότητα, άρα
και εφαρμόζοντας την, έχουμε ισότητα, άρα  .
. δεν είναι
δεν είναι  , έχουμε δύο περιπτώσεις. Αν
, έχουμε δύο περιπτώσεις. Αν  :
:  άρα τελικά όλα τα
άρα τελικά όλα τα  είναι ίσα, οπότε
είναι ίσα, οπότε  , άτοπο.
, άτοπο. είναι άτοπο, άρα
είναι άτοπο, άρα  , και μπορούμε εύκολα να κάνουμε μία κατασκευή, π.χ.
, και μπορούμε εύκολα να κάνουμε μία κατασκευή, π.χ. 
 φορές.
φορές. είναι η μόνη λύση στο πρόβλημα.
είναι η μόνη λύση στο πρόβλημα. πολλαπλάσιο του
πολλαπλάσιο του  γίνεται αν πάρουμε την ακολουθία
γίνεται αν πάρουμε την ακολουθία  . Ας υποθέσουμε λοιπόν ότι
. Ας υποθέσουμε λοιπόν ότι  .
. για κάθε
για κάθε  . (Όπου
. (Όπου  .)
.)
 για κάθε
για κάθε  . Επειδή
. Επειδή  . Έστω
. Έστω  . Τότε
. Τότε  . Αλλά
. Αλλά  , άτοπο.
, άτοπο.  .
.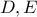 ταυτίζεται με τα
ταυτίζεται με τα  αντίστοιχα.
αντίστοιχα.  τέμνει τον περιγεγραμμένο κύκλο του
τέμνει τον περιγεγραμμένο κύκλο του  .
. .
. είναι ισοσκελές, με
είναι ισοσκελές, με  .
.  τέμνει τον περιγεγραμμένο κύκλο του
τέμνει τον περιγεγραμμένο κύκλο του  .
.  , δηλαδή
, δηλαδή  .
. , ενώ
, ενώ  (αφού η
(αφού η  είναι επίκεντρη της
είναι επίκεντρη της  στο κύκλο με κέντρο
στο κύκλο με κέντρο  και ακτίνα
και ακτίνα  , δηλαδή
, δηλαδή  .
. , από τον ορισμό του
, από τον ορισμό του  .
. είναι εγγράψιμο και
είναι εγγράψιμο και  , άρα η
, άρα η  είναι η διχοτόμος της
είναι η διχοτόμος της 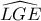 .
. δεν ήταν ισοσκελές, τότε αφού το
δεν ήταν ισοσκελές, τότε αφού το  , θα έπρεπε το
, θα έπρεπε το  να είναι εγγράψιμο (θεώρημα νότιου πόλου), άτοπο, αφού ο περιγεγραμμένος κύκλος του
να είναι εγγράψιμο (θεώρημα νότιου πόλου), άτοπο, αφού ο περιγεγραμμένος κύκλος του  είναι ο περιγεγραμμένος κύκλος του
είναι ο περιγεγραμμένος κύκλος του  ,
,  είναι το σημείο τομής των
είναι το σημείο τομής των  και
και 
![d=2h_1-b=2\left[\frac12\left(a+b+f-\frac{ab}{f}\right)\right] - b = a+f-\frac{ab}{f} d=2h_1-b=2\left[\frac12\left(a+b+f-\frac{ab}{f}\right)\right] - b = a+f-\frac{ab}{f}](/forum/ext/geomar/texintegr/latexrender/pictures/083a626a43191a28c9cc252e81fa7c0a.png)







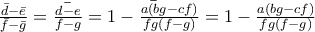


 και
και  (είναι φανερό)
(είναι φανερό) ειναι πάνω στα τόξα
ειναι πάνω στα τόξα  και
και  δηλαδή είανι τα ίσα κλάσματα είανι το σημείο Α
δηλαδή είανι τα ίσα κλάσματα είανι το σημείο Α που είανι ακριβώς η περίπτωση 1.
που είανι ακριβώς η περίπτωση 1. έχουμε το :
έχουμε το : είναι ο base.
είναι ο base. .
. , άρα
, άρα  , οπότε καταλήγουμε ότι αν
, οπότε καταλήγουμε ότι αν  , άρα και για
, άρα και για  είναι αδύνατο να κατασκευαστεί ένα αντι-Πασκάλ.
είναι αδύνατο να κατασκευαστεί ένα αντι-Πασκάλ. Άμεσα παρατηρούμε ότι
Άμεσα παρατηρούμε ότι 
 και
και  είναι αμβλυγώνια και ίσα, αφού έχουμε
είναι αμβλυγώνια και ίσα, αφού έχουμε  .
.  Συνεπώς
Συνεπώς  Όταν το σημείο
Όταν το σημείο  , τότε έχουμε ταύτιση των ευθειών
, τότε έχουμε ταύτιση των ευθειών 


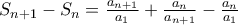 είναι ακέραιος.
είναι ακέραιος. 
 για τον μέγιστο κοινό διαιρέτη των
για τον μέγιστο κοινό διαιρέτη των  . Θα δείξω αρχικά ότι
. Θα δείξω αρχικά ότι  .
. ώστε
ώστε  και
και 

 για κάθε
για κάθε  .
. είναι ίσα με
είναι ίσα με  για
για  και
και  για
για  για κάθε
για κάθε 
 και επειδή
και επειδή  , τότε
, τότε  .
. ώστε
ώστε  για κάθε
για κάθε  για κάθε
για κάθε