Πρόβλημα 1.
Θεωρούμε τετράπλευρο
 εγγεγραμμένο σε κύκλο
εγγεγραμμένο σε κύκλο  με
με  και όπου η
και όπου η  δεν είναι παράλληλη στην
δεν είναι παράλληλη στην  . Οι διαγώνιοι
. Οι διαγώνιοι  και
και  τέμνονται στο σημείο
τέμνονται στο σημείο  και το σημείο
και το σημείο  είναι το ίχνος της καθέτου από το
είναι το ίχνος της καθέτου από το  στο τμήμα
στο τμήμα  . Αν η
. Αν η 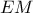 είναι διχοτόμος της γωνίας
είναι διχοτόμος της γωνίας  , να αποδείξετε ότι η
, να αποδείξετε ότι η  είναι διάμετρος του κύκλου
είναι διάμετρος του κύκλου  .
.Πρόβλημα 2.
Θεωρούμε ένα θετικό ρητό
 . Δύο μυρμήγκια βρίσκονται αρχικά στο ίδιο σημείο
. Δύο μυρμήγκια βρίσκονται αρχικά στο ίδιο σημείο  του επιπέδου. Στο
του επιπέδου. Στο  -οστό λεπτό (
-οστό λεπτό ( ) κάθε ένα από αυτά επιλέγει αν θα κινηθεί βόρεια, νότια, ανατολικά ή δυτικά και μετακινείται
) κάθε ένα από αυτά επιλέγει αν θα κινηθεί βόρεια, νότια, ανατολικά ή δυτικά και μετακινείται  μέτρα προς αυτήν την κατεύθυνση. Αν μετά από ακέραιο αριθμό λεπτών τα δύο μυρμήγκια βρεθούν στο ίδιο σημείο του επιπέδου (όχι απαραίτητα στο
μέτρα προς αυτήν την κατεύθυνση. Αν μετά από ακέραιο αριθμό λεπτών τα δύο μυρμήγκια βρεθούν στο ίδιο σημείο του επιπέδου (όχι απαραίτητα στο  ), χωρίς να έχουν ακολουθήσει ακριβώς την ίδια διαδρομή, να προσδιορίσετε όλες τις δυνατές τιμές του
), χωρίς να έχουν ακολουθήσει ακριβώς την ίδια διαδρομή, να προσδιορίσετε όλες τις δυνατές τιμές του  .
. Πρόβλημα 3.
Ο Σιλουανός και ο Δημήτρης παίζουν το ακόλουθο παιγνίδι έχοντας αρχικά δύο μη κενές στοίβες νομισμάτων: Εναλλάξ, με τον Σιλουανό να ξεκινάει πρώτος, κάθε παίκτης διαλέγει μία στοίβα με άρτιο αριθμό νομισμάτων και μετακινεί τα μισά νομίσματα αυτής της στοίβας στην άλλη. Το παιγνίδι τερματίζεται όταν κάποιος από τους παίκτες δεν μπορεί να κάνει κίνηση. Σε αυτήν την περίπτωση κερδίζει ο άλλος παίκτης.
Να προσδιορίσετε όλα τα ζεύγη θετικών ακεραίων
 ώστε αν αρχικά οι δύο στοίβες έχουν από
ώστε αν αρχικά οι δύο στοίβες έχουν από  και
και  νομίσματα αντίστοιχα, τότε ο Δημήτρης έχει στρατηγική νίκης.
νομίσματα αντίστοιχα, τότε ο Δημήτρης έχει στρατηγική νίκης.Πρόβλημα 4.
Να βρείτε όλους τους πρώτους αριθμούς
 και
και  ώστε ο
ώστε ο  να διαιρεί τον
να διαιρεί τον  .
.
 είναι το σημείο τομής των
είναι το σημείο τομής των  τότε είναι άμεσα θεωρικά γνωστό λόγω της διχοτόμησης της γωνίας
τότε είναι άμεσα θεωρικά γνωστό λόγω της διχοτόμησης της γωνίας 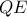 στην οποία ανήκει και το
στην οποία ανήκει και το  Αν τώρα θεωρήσουμε την ευθεία
Αν τώρα θεωρήσουμε την ευθεία  , με
, με  διάμετρο επίσης αυτή θα είναι κάθετη στην ίδια πολική. Άρα οι
διάμετρο επίσης αυτή θα είναι κάθετη στην ίδια πολική. Άρα οι  θα ταυτίζονται, λόγω του μονοσημάντου της κάθετης σημείου σε ευθεία.
θα ταυτίζονται, λόγω του μονοσημάντου της κάθετης σημείου σε ευθεία. είναι το κέντρο του κύκλου. Έστω πως η
είναι το κέντρο του κύκλου. Έστω πως η  και η
και η  . Επειδή
. Επειδή  και η
και η  διχοτομεί την
διχοτομεί την  , έχουμε πως η τετράδα
, έχουμε πως η τετράδα  είναι αρμονική. Άρα το
είναι αρμονική. Άρα το  , δηλαδή η
, δηλαδή η  .
. . Όμως
. Όμως  , άρα το
, άρα το 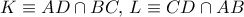 . Επίσης, έστω
. Επίσης, έστω  .
. , ισχύει
, ισχύει  .
. έχουμε ότι
έχουμε ότι  , άρα
, άρα  συμπίπτουν.
συμπίπτουν. είναι συνευθειακά.
είναι συνευθειακά. και έστω
και έστω  .
.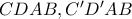 έχουμε τις ισότητες των πράσινων γωνιών, άρα
έχουμε τις ισότητες των πράσινων γωνιών, άρα  (1).
(1). (2).
(2). (όπου
(όπου  ) είναι
) είναι  (3).
(3). , και αφού
, και αφού  .
. διάμετρος του κύκλου
διάμετρος του κύκλου  .
. .
. ένας περιττός πρώτος διαιρέτης του
ένας περιττός πρώτος διαιρέτης του  , ο
, ο 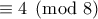 , και αφού
, και αφού  , θα έχει αναγκαστικά έναν πρώτο (περιττό) διαιρέτη. Αν τώρα
, θα έχει αναγκαστικά έναν πρώτο (περιττό) διαιρέτη. Αν τώρα  , ο
, ο  είναι περιττός, και προφανώς έχει έναν πρώτο περιττό διαιρέτη).
είναι περιττός, και προφανώς έχει έναν πρώτο περιττό διαιρέτη). .
. να είναι το
να είναι το  .
. , είναι
, είναι 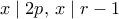 .
. .
.  , τότε αν
, τότε αν  , είναι
, είναι  , άτοπο, αφού ο
, άτοπο, αφού ο  . Αν επίσης
. Αν επίσης  , έχουμε ομοίως άτοπο.
, έχουμε ομοίως άτοπο.  ή
ή  .
. , αφού
, αφού  .
. (αφού
(αφού  ). Από το LTE, είναι
). Από το LTE, είναι  , επομένως
, επομένως  , και όμοια
, και όμοια  . Παίρνοντας τις περιπτώσεις, έχουμε τη λύση
. Παίρνοντας τις περιπτώσεις, έχουμε τη λύση 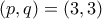 .
. , και άρα
, και άρα 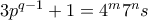 , με
, με  . Όπως πριν,
. Όπως πριν,  , και άρα παίρνοντας
, και άρα παίρνοντας  , έχουμε
, έχουμε 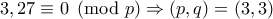 .
. . Τότε,
. Τότε,  . Αν ο
. Αν ο  έχει έναν περιττό πρώτο διαιρέτη, έστω
έχει έναν περιττό πρώτο διαιρέτη, έστω  , και αφού
, και αφού  .
.  . Αφού
. Αφού 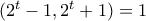 , είναι
, είναι  ή
ή  . Και οι δύο περιπτώσεις δίνουν εύκολα άτοπο. (η πρώτη δίνει
. Και οι δύο περιπτώσεις δίνουν εύκολα άτοπο. (η πρώτη δίνει  , άτοπο, και η δεύτερη
, άτοπο, και η δεύτερη  , που δεν επαληθεύει).
, που δεν επαληθεύει). .
. θέσεις με συντεταγμένες
θέσεις με συντεταγμένες  και
και  . Ορίζουμε
. Ορίζουμε  .
. αναφερόμαστε στο
αναφερόμαστε στο  όπου
όπου  και
και  οι θέσεις των μυρμηγκιών τη χρονική στιγμή
οι θέσεις των μυρμηγκιών τη χρονική στιγμή  .
.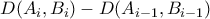 είναι
είναι  ή
ή  ή
ή  . Αυτό ισχύει επειδή από τη χρονική στιγμή
. Αυτό ισχύει επειδή από τη χρονική στιγμή  στην
στην  το
το  μεταβάλλεται κατά
μεταβάλλεται κατά  . Το ίδιο και το
. Το ίδιο και το  . Επομένως η διαφορά τους μεταβάλλεται κατά
. Επομένως η διαφορά τους μεταβάλλεται κατά  ή μένει σταθερή.
ή μένει σταθερή. , αλλά
, αλλά  , αφού η συνάντηση δεν είχε γίνει ήδη από τη στιγμή
, αφού η συνάντηση δεν είχε γίνει ήδη από τη στιγμή  -οστό λεπτό.
-οστό λεπτό. .
. -οστό λεπτό τα μυρμήγκια ακολουθούν την ίδια διαδρομή. Αυτό σημαίνει πως
-οστό λεπτό τα μυρμήγκια ακολουθούν την ίδια διαδρομή. Αυτό σημαίνει πως  . Όμως αφού μετά θα αλλάξουν διαδρομή θα ισχύει ότι
. Όμως αφού μετά θα αλλάξουν διαδρομή θα ισχύει ότι  .
. , όπου
, όπου  .
.
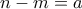 .
.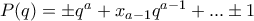
 με
με  .
. και
και  , άρα
, άρα  (απορρίπτεται) και
(απορρίπτεται) και  .
. .
. και έστω
και έστω  .Για όλες τις θέσεις, εκτός από όταν
.Για όλες τις θέσεις, εκτός από όταν  (είτε στην αρχή είτε κατά τη διάρκεια του παιχνιδιού) οι 2 κινήσεις μεταβάλλουν τα
(είτε στην αρχή είτε κατά τη διάρκεια του παιχνιδιού) οι 2 κινήσεις μεταβάλλουν τα  ως εξής:
ως εξής: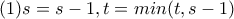 και
και  .Ονομάζω κατάσταση
.Ονομάζω κατάσταση  την κατάσταση όπου οι αριθμοί είναι ίδιοι(είτε στην αρχή είτε κατά τη διάρκεια του παιχνιδιού).
την κατάσταση όπου οι αριθμοί είναι ίδιοι(είτε στην αρχή είτε κατά τη διάρκεια του παιχνιδιού). κερδίζει πάντα ο Σιλουανός γιατί με την κίνηση
κερδίζει πάντα ο Σιλουανός γιατί με την κίνηση  φέρνει το παιχνίδι σε κατάσταση
φέρνει το παιχνίδι σε κατάσταση  ,όποιος φέρει το παιχνίδι σε κατάσταση
,όποιος φέρει το παιχνίδι σε κατάσταση  .Την κρίσιμη στιγμή όπου
.Την κρίσιμη στιγμή όπου  ,με μείωση του
,με μείωση του  η μικρότερη εκ των 2 τιμή που θα προκύψει θα είναι ίδια με πριν, ενώ η μεγαλύτερη πιθανώς να αλλάξει ανεξέλεγκτα.Για αποφυγή ήττας,οι δύο παίκτες θα εξακολουθούν να παίζουν με τον ίδιο τρόπο και το παιχνίδι δε θα έχει νικητή.Η μόνη περίπτωση που κερδίζει ο Δημήτρης είναι αν το παιχνίδι αρχίσει σε κατάσταση
η μικρότερη εκ των 2 τιμή που θα προκύψει θα είναι ίδια με πριν, ενώ η μεγαλύτερη πιθανώς να αλλάξει ανεξέλεγκτα.Για αποφυγή ήττας,οι δύο παίκτες θα εξακολουθούν να παίζουν με τον ίδιο τρόπο και το παιχνίδι δε θα έχει νικητή.Η μόνη περίπτωση που κερδίζει ο Δημήτρης είναι αν το παιχνίδι αρχίσει σε κατάσταση  .Το παιχνίδι φανερά δεν τελειώνει ποτέ.
.Το παιχνίδι φανερά δεν τελειώνει ποτέ. .Φανερά κερδίζει ο Δημήτρης.
.Φανερά κερδίζει ο Δημήτρης. και για τέτοια ώστε
και για τέτοια ώστε  .
.
 .
.
 ; Ότι κάθε στήλη έχει το ίδιο πλήθος νομισμάτων;
; Ότι κάθε στήλη έχει το ίδιο πλήθος νομισμάτων;  για τους μιγαδικούς αριθμούς που δηλώνουν την μετακίνηση των μυρμηγκιών στο
για τους μιγαδικούς αριθμούς που δηλώνουν την μετακίνηση των μυρμηγκιών στο  για κάποιο
για κάποιο  . Αν τα μυρμήγκια συναντηθούν στο
. Αν τα μυρμήγκια συναντηθούν στο 
 παίρνουμε ένα πολυώνυμο
παίρνουμε ένα πολυώνυμο  με συντελεστές στο σύνολο
με συντελεστές στο σύνολο  ώστε
ώστε  . Το πολυώνυμο δεν είναι το μηδενικό και από το θεώρημα ρητών ριζών στο
. Το πολυώνυμο δεν είναι το μηδενικό και από το θεώρημα ρητών ριζών στο ![\mathbb{Z} \left[i\right] \mathbb{Z} \left[i\right]](/forum/ext/geomar/texintegr/latexrender/pictures/1f0ad19f6194bcb0757c3daff471bda8.png) (ίδια απόδειξη με πολυώνυμα στους ακεραίους) πρέπει
(ίδια απόδειξη με πολυώνυμα στους ακεραίους) πρέπει  όπου τα
όπου τα  . Όμως το
. Όμως το