Ανοιχτή Ολυμπιάδα ΦΜΛ 239 (8/9η τάξη 2012)

Al.Koutsouridis · #1

Ανοιχτή Ολυμπιάδα Φυσικομαθηματικού Λυκείου 239 Αγίας Πέτρούπολης για τις τάξεις 8η και 9η , 2012

1. Σε σκακιέρα $12 \times 12$ είναι τοποθετημένοι μερικοί ίπποι, εξάλλου σε κάθε τετράγωνο $2 \times 2$ είναι τοποθετημένος τουλάχιστον ένας ίππος. Ποιο είναι το ελάχιστο πλήθος κελιών που απειλούν αυτοί οι ίπποι; (ο ίππος δεν απειλεί το κελί στο οποίο είναι τοποθετημένος, αλλά μπορεί να απειλεί κελιά στα οποία είναι τοποθετημένοι άλλοι ίπποι.)

2. Δίνονται θετικοί ακέραιοι αριθμοί a > b

και

. Αποδείξτε, ότι αν a+b+c+d=ab-cd

, τότε ο αριθμός a+c

θα είναι σύνθετος.

3. Στο επίπεδο δίνονται

σημεία, ανά τρία μη συνευθειακά. Μπορούμε να διαλέξουμε δυο σημεία

και

και να μεταφέρουμε το σημείο

στο μέσο του τμήματος

. Προέκυψε, ότι με τέτοιες μεταφορές, τα σημεία κατέλαβαν τις ίδιες θέσεις (πιθανόν με διαφορετική σειρά). Για ποιο ελάχιστο

θα μπορούσε να συμβεί κάτι τέτοιο;

4. Το άθροισμα των θετικών αριθμών a,b

και

είναι ίσο με

. Αποδείξτε την ανίσωση

$(a-b)^2+(b-c)^2+(c-a)^2 \geq \dfrac{1-27abc}{2}$ .

5. Στην υποτείνουσά

ορθογωνίου τριγώνου ABC

δίνεται σημείο

, ώστε

. Έστω

σημείο της καθέτου από το σημείο

προς την ευθεία

, που ισαπέχει από τα σημεία

και

. Επίσης, έστω

το μέσο του τμήματος

. Αποδείξτε, ότι η ευθεία

εφάπτεται του περιγεγραμμένου κύκλου του τριγώνου BLP

.

6. Έστω

επίπεδος γράφος, όλες οι κορυφές του οποίου έχουν βαθμό

. Ο Βασίλης και ο Πέτρος κινούνται κατά μήκος των ακμών του. Την πρώτη φορά ο καθένας τους κινείται τυχαία, μετά όμως ο καθένας τους κινείται ευθεία (από τα τρία μονοπάτια διαλέγει το μεσαίο). Στο τέλος σε κάθε κορυφή υπήρξε ακριβώς ένας από αυτούς και ακριβώς μια φορά. Να αποδείξετε, ότι ο γράφος έχει άρτιο αριθμό κορυφών.

7. Δίνεται περιγεγραμμένο τετράπλευρο ABCD

. Είναι γνωστό, ότι $\angle ACB \neq \angle ACD$ . Στην διχοτόμο της γωνίας

διαλέγουμε σημείο

, τέτοιο ώστε $AE \perp BD$ . Το σημείο

είναι το ίχνος της καθέτου από το σημείο

προς την πλευρά

. Αποδείξτε, ότι AB=BF

.

8. Ο Νίκος σκέφτηκε ένα διψήφιο αριθμό

και ο Γιώργος προσπαθεί να τον μαντέψει. Για να το πετύχει ανακοινώνει έναν φυσικό αριθμό

και ο Νίκος κοινοποιεί στον Γιώργο το άθροισμα των ψηφίων του αριθμού

. Για ποιο ελάχιστο πλήθος ερωτήσεων ο Γιώργος εγγυημένα θα μαντέψει σωστά τον αριθμό;

Πηγή

Ορέστης Λιγνός · #2

Al.Koutsouridis έγραψε: ↑
Κυρ Απρ 15, 2018 1:17 pm
Ανοιχτή Ολυμπιάδα Φυσικομαθηματικού Λυκείου 239 Αγίας Πέτρούπολης για τις τάξεις 8η και 9η , 2012

4. Το άθροισμα των θετικών αριθμών και είναι ίσο με . Αποδείξτε την ανίσωση

$(a-b)^2+(b-c)^2+(c-a)^2 \geq \dfrac{1-27abc}{2}$ .

Πηγή

Η ανισότητα αναπτυγμένη γράφεται $2(a^2+b^2+c^2)-2(ab+bc+ca) \geqslant \dfrac{1-27abc}{2}$ , ή αλλιώς, αφού $\displaystyle \sum_{cyc} a^2=1-2\sum_{cyc} ab$ , $\displaystyle 1-6\sum_{\cyc} ab \geqslant \dfrac{1-27abc}{2} \Rightarrow 4\sum_{cyc} ab \leqslant 9abc+1$ , που είναι άμεση εφαρμογή της ανισότητας Schur $(a+b+c)^3+9abc \geqslant 4(a+b+c)(ab+bc+ca)$ .

Ορέστης Λιγνός · #3

Al.Koutsouridis έγραψε: ↑
Κυρ Απρ 15, 2018 1:17 pm
Ανοιχτή Ολυμπιάδα Φυσικομαθηματικού Λυκείου 239 Αγίας Πέτρούπολης για τις τάξεις 8η και 9η , 2012

5. Στην υποτείνουσά ορθογωνίου τριγώνου δίνεται σημείο , ώστε . Έστω σημείο της καθέτου από το σημείο προς την ευθεία , που ισαπέχει από τα σημεία και . Επίσης, έστω το μέσο του τμήματος . Αποδείξτε, ότι η ευθεία εφάπτεται του περιγεγραμμένου κύκλου του τριγώνου .

Φέρνουμε $AM \perp BP$ .

Αρκεί να δείξουμε πως $\widehat{LBP}=\widehat{APL}$ .

Είναι $BL, PK \perp LM \Rightarrow PK \parallel BL \Rightarrow \widehat{LBP}=\widehat{KPM}$ .

Αρκεί λοιπόν $\widehat{KPM}=\widehat{APL} \Rightarrow \widehat{LPK}=\widehat{APM}$ .

Από τα όμοια τρίγωνα $\vartriangle PKM, \,\, \vartriangle BLM$ , είναι $\dfrac{BL}{BM}=\dfrac{PK}{PM}$ (1).

Επίσης, αφού $PB=PK, PK \parallel BL \Rightarrow \widehat{MBA} \widehat{PBK}=\widehat{PKB}=\widehat{LBK} \Rightarrow \widehat{LBK}=\widehat{ABM}$ , και άρα τα ορθογώνια τρίγωνα $\vartriangle LBK, \vartriangle ABM$ είναι όμοια.

Έτσι, $\dfrac{BL}{BM}=\dfrac{LK}{MA}$ , και από (1), $\dfrac{LK}{MA}=\dfrac{PK}{PM}$ (2).

Από (2), και αφού τα τρίγωνα $\vartriangle LPK, \vartriangle PMA$ είναι ορθογωνία, αυτά τα δύο τρίγωνα είναι όμοια.

Άρα, $\widehat{LPK}=\widehat{APM}$ , ό.έ.δ.

Υ.Γ. Συγγνώμη για την έλλειψη σχήματος. Με την πρώτη ευκαιρία θα το προσθέσω. Αν κάποιος μπορεί ας το βάλει. Ευχαριστώ πολύ!

#4

Ορέστης Λιγνός έγραψε: ↑
Δευ Απρ 16, 2018 12:09 am

Al.Koutsouridis έγραψε: ↑
Κυρ Απρ 15, 2018 1:17 pm
Ανοιχτή Ολυμπιάδα Φυσικομαθηματικού Λυκείου 239 Αγίας Πέτρούπολης για τις τάξεις 8η και 9η , 2012

5. Στην υποτείνουσά ορθογωνίου τριγώνου δίνεται σημείο , ώστε . Έστω σημείο της καθέτου από το σημείο προς την ευθεία , που ισαπέχει από τα σημεία και . Επίσης, έστω το μέσο του τμήματος . Αποδείξτε, ότι η ευθεία εφάπτεται του περιγεγραμμένου κύκλου του τριγώνου .

Φέρνουμε $AM \perp BP$ .

Αρκεί να δείξουμε πως $\widehat{LBP}=\widehat{APL}$ .

Είναι $BL, PK \perp LM \Rightarrow PK \parallel BL \Rightarrow \widehat{LBP}=\widehat{KPM}$ .

Αρκεί λοιπόν $\widehat{KPM}=\widehat{APL} \Rightarrow \widehat{LPK}=\widehat{APM}$ .

Από τα όμοια τρίγωνα $\vartriangle PKM, \,\, \vartriangle BLM$ , είναι $\dfrac{BL}{BM}=\dfrac{PK}{PM}$ (1).

Επίσης, αφού $PB=PK, PK \parallel BL \Rightarrow \widehat{MBA} \widehat{PBK}=\widehat{PKB}=\widehat{LBK} \Rightarrow \widehat{LBK}=\widehat{ABM}$ , και άρα τα ορθογώνια τρίγωνα $\vartriangle LBK, \vartriangle ABM$ είναι όμοια.

Έτσι, $\dfrac{BL}{BM}=\dfrac{LK}{MA}$ , και από (1), $\dfrac{LK}{MA}=\dfrac{PK}{PM}$ (2).

Από (2), και αφού τα τρίγωνα $\vartriangle LPK, \vartriangle PMA$ είναι ορθογωνία, αυτά τα δύο τρίγωνα είναι όμοια.

Άρα, $\widehat{LPK}=\widehat{APM}$ , ό.έ.δ.

Υ.Γ. Συγγνώμη για την έλλειψη σχήματος. Με την πρώτη ευκαιρία θα το προσθέσω. Αν κάποιος μπορεί ας το βάλει. Ευχαριστώ πολύ!

Δίνω το σχήμα.

: Ο.Λ.png (32.92 KiB) Προβλήθηκε 1701 φορές

#5

Al.Koutsouridis έγραψε: ↑
Κυρ Απρ 15, 2018 1:17 pm
2. Δίνονται θετικοί ακέραιοι αριθμοί και . Αποδείξτε, ότι αν , τότε ο αριθμός θα είναι σύνθετος.

Πάρα πολύ ωραία όλα τα θέματα. Για την παραπάνω:

Η συνθήκη γράφεται $\displaystyle{(c+1)(d+1)=(a-1)(b-1)}$ . Αν τα c+1, a-1

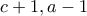ήσαν πρώτα προς αλλήλους τότε θα είχαμε c+1|b-1

και

.

Αλλά τότε από την a>b

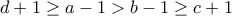θα είχαμε $d+1\ge a-1>b-1\ge c+1$ , που αντιβαίνει στην υπόθεση c>d

.

Τελικά τα c+1, a-1

έχουν κοινό διαιρέτη p>1

και άρα $c+1=pq, \, a-1=pr$ για κάποια q,r

.

Έπεται ότι a+c=(a-1)+(c+1)=pr+pq=p(q+r)=

σύνθετος.

Ορέστης Λιγνός · #6

Al.Koutsouridis έγραψε: ↑
Κυρ Απρ 15, 2018 1:17 pm
Ανοιχτή Ολυμπιάδα Φυσικομαθηματικού Λυκείου 239 Αγίας Πέτρούπολης για τις τάξεις 8η και 9η , 2012

7. Δίνεται περιγεγραμμένο τετράπλευρο . Είναι γνωστό, ότι $\angle ACB \neq \angle ACD$ . Στην διχοτόμο της γωνίας διαλέγουμε σημείο , τέτοιο ώστε $AE \perp BD$ . Το σημείο είναι το ίχνος της καθέτου από το σημείο προς την πλευρά . Αποδείξτε, ότι .

Φέρνουμε $EK \perp CD$ .

Από την προφανή ισότητα των $\vartriangle CKE, \vartriangle CFE$ έχουμε EK=EF

.

Το Π.Θ. στα τρίγωνα $\vartriangle DEK, \vartriangle BEF$ , δίνει ED^2=EK^2+KD^2

και

.

Με αφαίρεση κατά μέλη των δύο παραπάνω (χρησιμοποιούμε EF=EK

) έχουμε

(1).

Από το κριτήριο καθετότητας EB^2-ED^2=AB^2-AD^2

(2).

Από (1), (2) DK^2-BF^2=AD^2-AB^2

(3).

Όμως, αφού και το ABCD

είναι περιγεγραμμένο, έχουμε AD-AB=CD-CB=(DK+KC)-(BF+FC)=DK-BF

, αφού επίσης CK=CF

(από τα ίσα $\vartriangle CEK, \vartriangle CEF$ ).

Έτσι, AD-AB=DK-BF

(4).

Συνδυάζοντας τις (3), (4), (AD-AB)(AD+AB)=AD^2-AB^2=DK^2-BF^2=(DK-BF)(DK+BF)=

$(AD-AB)(DK+BF) \Rightarrow DK+BF=AD+AB=(AD-AB)+2AB=DK-BF+2AB$

$\Rightarrow AB=BF$ , και το ζητούμενο έχει αποδειχθεί.

: ISA.png (26.07 KiB) Προβλήθηκε 1637 φορές

#7

Al.Koutsouridis έγραψε: ↑
Κυρ Απρ 15, 2018 1:17 pm
Ανοιχτή Ολυμπιάδα Φυσικομαθηματικού Λυκείου 239 Αγίας Πέτρούπολης για τις τάξεις 8η και 9η , 2012

3. Στο επίπεδο δίνονται σημεία, ανά τρία μη συνευθειακά. Μπορούμε να διαλέξουμε δυο σημεία και και να μεταφέρουμε το σημείο στο μέσο του τμήματος . Προέκυψε, ότι με τέτοιες μεταφορές, τα σημεία κατέλαβαν τις ίδιες θέσεις (πιθανόν με διαφορετική σειρά). Για ποιο ελάχιστο θα μπορούσε να συμβεί κάτι τέτοιο;

Πρέπει $n \geqslant 3$ αφού για n=2

αυτό είναι αδύνατο.

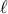Έστω ευθεία $\ell$ ώστε ένα από τα σημεία, έστω το

, να είναι πάνω στην $\ell$ και όλα τα υπόλοιπα είναι από την μία μεριά της $\ell$ . Αυτό εξακολουθεί να ισχύει μετά από κάθε μεταφορά. Μάλιστα απαγορεύεται να μεταφερθεί το

αφού τότε όλα τα σημεία θα είναι πάντα από την μία μεριά της $\ell$ .

Θεωρούμε τώρα την κυρτή θήκη του συνόλου των σημείων. Επειδή έχουμε πεπερασμένο αριθμό σημείων, ανά τρία μη συνευθειακά, αυτή θα είναι ένα πολύγωνο. Οι κορυφές του είναι κάποια από τα δοθέντα σημεία και από την παρατήρηση της προηγούμενης παραγράφου αυτά απαγορεύονται να μεταφερθούν.

Άρα πρέπει απαραίτητα $n \geqslant 4$ . Για n=4

μπορούμε να πάρουμε τα σημεία A=(-3,0),B=(3,0),C=(1,7)

και

.

Διαλέγουμε πρώτα τα D,A

και μεταφέρουμε το

στο

.
Διαλέγουμε μετά τα D,Β

και μεταφέρουμε το

στο

.
Τέλος διαλέγουμε τα D,Ψ

και μεταφέρουμε το

στο

, δηλαδή στην αρχική του θέση.

S.E.Louridas · #8

Al.Koutsouridis έγραψε: ↑
Κυρ Απρ 15, 2018 1:17 pm
Ανοιχτή Ολυμπιάδα Φυσικομαθηματικού Λυκείου 239 Αγίας Πέτρούπολης για τις τάξεις 8η και 9η , 2012
7. Δίνεται περιγεγραμμένο τετράπλευρο . Είναι γνωστό, ότι $\angle ACB \neq \angle ACD$ . Στην διχοτόμο της γωνίας διαλέγουμε σημείο , τέτοιο ώστε $AE \perp BD$ . Το σημείο είναι το ίχνος της καθέτου από το σημείο προς την πλευρά . Αποδείξτε, ότι .

Καταρχάς ευχαριστώ πολύ τον Αλέξανδρο Κουτσουρίδη που μου επεσήμανε ένα μη εξηγήσιμο σημείο στην προηγούμενη λύση μου την οποία και αντικαθιστώ με αυτή που ακολουθεί. Επισημαίνω επίσης ότι με εντυπωσίασε η λύση του Ορέστη.

Θεωρούμε χωρίς βλάβη της γενικότητας AB < BC.

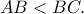Με μία απλή εφαρμογή του θεωρήματος Μενελάου στα τρίγωνα ADB, BDC

, βλέπουμε ότι οι ευθείες $ZH,\;LJ,\;DB$ συγκλίνουν στο

(

είναι σημεία επαφής του εγγεγραμμένου κύκλου με τις πλευρές). Προφανώς το

είναι ριζικό κέντρο των $c,\;{c_1},\;{d_1},$ με αντίστοιχα κέντρα τα I,A,C.

Αν επί της

θεωρήσουμε σημείο

τέτοιο που οι προβολή του F_1

στην

να έχει τη ιδιότητα $B{F_1}=BA,$ τότε θα ισχύει $BH \cdot B{H_1} = BJ \cdot B{J_1},$ που σημαίνει ότι το

θα ανήκει στον ριζικό άξονα των $\ {c_1}, {p_1}$ με κέντρα A, N

αντίστοιχα με το

να ανήκει επίσης στον ίδιο ριζικό άξονα. Άρα $VB \bot AN \Rightarrow N \equiv E.$ Εδώ θεωρώ ότι το πρόβλημα τελείωσε. Αν AB=BC,

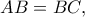τότε η λύση είναι σχεδόν άμεση.

: ασδφγ.png (22.38 KiB) Προβλήθηκε 1416 φορές

Ανοιχτή Ολυμπιάδα ΦΜΛ 239 (8/9η τάξη 2012)

Ανοιχτή Ολυμπιάδα ΦΜΛ 239 (8/9η τάξη 2012)

Re: Ανοιχτή Ολυμπιάδα ΦΜΛ 239 (8/9η τάξη 2012)

Re: Ανοιχτή Ολυμπιάδα ΦΜΛ 239 (8/9η τάξη 2012)

Re: Ανοιχτή Ολυμπιάδα ΦΜΛ 239 (8/9η τάξη 2012)

Re: Ανοιχτή Ολυμπιάδα ΦΜΛ 239 (8/9η τάξη 2012)

Re: Ανοιχτή Ολυμπιάδα ΦΜΛ 239 (8/9η τάξη 2012)

Re: Ανοιχτή Ολυμπιάδα ΦΜΛ 239 (8/9η τάξη 2012)

Re: Ανοιχτή Ολυμπιάδα ΦΜΛ 239 (8/9η τάξη 2012)

Μέλη σε σύνδεση