EGMO 2018/4

#1

Ένα ντόμινο είναι ένα $2 \times 1$ ή $1 \times 2$ πλακάκι.

Έστω ακέραιος $n \geqslant 3$ . Σε έναν $n \times n$ πίνακα τοποθετούμε ντόμινο με τέτοιο τρόπο ώστε καθένα από αυτά να καλύπτει ακριβώς δύο κελιά του πίνακα και τα ντόμινο μεταξύ τους να μην αλληλοκαλύπτονται.

Ορίζουμε ως τιμή μιας γραμμής ή στήλης το πλήθος των ντόμινο που καλύπτουν τουλάχιστον ένα κελί αυτής της γραμμής ή της στήλης. Ονομάζουμε την τοποθέτηση των ντόμινο ισορροπημένη εάν υπάρχει κάποιος $k \geqslant 1$ τέτοιος ώστε η τιμή κάθε γραμμής και κάθε στήλης να είναι

.

Αποδείξτε πως για κάθε $n \geqslant 3$ υπάρχει κάποια ισορροπημένη τοποθέτηση και βρείτε τον ελάχιστο αριθμό των ντόμινο που απαιτείται για μια τέτοια τοποθέτηση.

dement · #2

Ο συμβολισμός $(m,n, \Delta)$ σημαίνει "πλακάκι με το ένα σημείο στο (m,n)

και το άλλο δεξιά του". Αντίστοιχα με

σημαίνει "κάτω".

Έστω ότι η τιμή κάθε στήλης και γραμμής είναι

. Τότε, αφού συνολικά υπάρχουν

στήλες και γραμμές και κάθε πλακάκι καλύπτει μία από την μία κατηγορία και δύο από την άλλη, θα πρέπει να υπάρχουν $\displaystyle \frac{2kn}{3}$ πλακάκια. Επομένως $3 \mid kn$ .

Έτσι, αν $3 \mid n$ , η ελάχιστη δυνατή τιμή είναι μεγαλύτερη ή ίση του

. Αυτό μπορεί να επιτευχθεί γεμίζοντας τους $3 \times 3$ υποπίνακες κατά μήκος της κύριας διαγωνίου με πλακάκια $(1,1,\Delta), (2,3,K)$ . Έτσι, χρειάζονται $\displaystyle \frac{2n}{3}$ πλακάκια.

Αν $3 \nmid n$ τότε προφανώς η ελάχιστη δυνατή τιμή είναι μεγαλύτερη ή ίση του

. Θα δείξουμε ότι είναι εφικτή.

Σε πίνακα $4 \times 4$ βάζουμε πλακάκια $(1,1,\Delta),(2,1,\Delta),(1,3,K),(1,4,K),(3,1,K),(3,2,K),(3,3,\Delta),(4,3,\Delta)$ .

Σε πίνακα $5 \times 5$ βάζουμε πλακάκια $(1,1,\Delta),(1,3,\Delta),(1,5,K),(3,5,K),(5,4,\Delta),(5,2,\Delta),(4,1,K),(2,1,K),(2,2,\Delta),(3,4,K)$ .

Σε πίνακα $7 \times 7$ βάζουμε πλακάκια $(1,1,\Delta),(1,3,\Delta),(1,5,\Delta),(2,1,\Delta),(2,4,\Delta),(2,7,K),(3,3,K),(3,6,K),(4,7,K),(5,1,\Delta),$
$\displaystyle (5,4,\Delta),(6,3,K),(6,6,K),(6,7,K)$ .

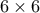Στους υπόλοιπους πίνακες γεμίζουμε τους $4 \times 4$ υποπίνακες κατά μήκος της κύριας διαγωνίου μέχρι να μας μείνει πίνακας $4 \times 4, 5 \times 5$ ή $7 \times 7$ . Αν μας μείνει $6 \times 6$ , τότε ξεκινάμε με πίνακα $5 \times 5$ και συνεχίζουμε με $4 \times 4$ μέχρι να μας μείνει $5 \times 5$ στο τέλος.Έτσι, χρειάζονται

πλακάκια.

EGMO 2018/4

EGMO 2018/4

Re: EGMO 2018/4

Μέλη σε σύνδεση