Σελίδα 1 από 2
ΠΡΟΚΡΙΜΑΤΙΚΟΣ 2018
Δημοσιεύτηκε: Κυρ Απρ 01, 2018 3:04 am
από Τσιαλας Νικολαος
Σήμερα είναι ο προκριματικός!!! Μετά το πέρας των εξετάσεων όποιος μπορεί ας βάλει τα θέματα, αν φυσικά δεν υπάρχει κάποιο πρόβλημα και ζητήσει η επιτροπή το αντιθέτο.


Re: ΠΡΟΚΡΙΜΑΤΙΚΟΣ 2018
Δημοσιεύτηκε: Κυρ Απρ 01, 2018 7:36 am
από Γιάννης Μπόρμπας
Καλή επιτυχία στους συμμετέχοντες!
Re: ΠΡΟΚΡΙΜΑΤΙΚΟΣ 2018
Δημοσιεύτηκε: Κυρ Απρ 01, 2018 3:35 pm
από JimNt.
Τα θέματα των μεγάλων δεν θα ανακοινωθούν , αφού μάλλον προέρχονται από Shortlists.
Re: ΠΡΟΚΡΙΜΑΤΙΚΟΣ 2018
Δημοσιεύτηκε: Κυρ Απρ 01, 2018 3:52 pm
από cretanman
Καλησπέρα σε όλους!
Γράφω τα θέματα των Μικρών.
Τα θέματα των μεγάλων
ΔΕΝ μπορούν να κοινοποιηθούν σήμερα για το λόγο ότι υπάρχουν μέσα σε αυτά θέματα από τη λίστα προβλημάτων (shortlist) διεθνών διαγωνισμών (που πρέπει να παραμείνει κρυφή μέχρι την επόμενη διοργάνωση) κι έτσι με δεδομένο ότι δεν έχει ολοκληρωθεί η διαδικασία επιλογής των ομάδων από όλες τις χώρες, τα θέματα ΔΕΝ πρέπει να γίνουν γνωστά. Αυτό έχει τονιστεί και στους διαγωνιζόμενους σήμερα.
Εύχομαι καλά αποτελέσματα σε όλους τους συμμετέχοντες!
Θέματα Μικρών:
1ο Θέμα
Θεωρούμε τους θετικούς πραγματικούς αριθμούς

που είναι τέτοιοι, ώστε

. Να αποδείξετε ότι υπάρχουν δύο από τους

με άθροισμα μεγαλύτερο ή ίσο του

.
2ο Θέμα
Δίνεται οξυγώνιο τρίγωνο

με

, ο περιγεγραμμένος κύκλος του

και τα μέσα

των πλευρών

και

αντίστοιχα. Με διαμέτρους τις πλευρές

και

θεωρούμε ημικύκλια, εξωτερικά του τριγώνου, τα οποία τέμνονται από την ευθεία

στα σημεία

και

αντίστοιχα. Οι ευθείες

και
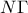
τέμνουν τον περιγεγραμμένο κύκλο στα σημεία

αντίστοιχα. Οι ευθείες

και
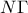
τέμνονται στο σημείο

. Να αποδείξετε ότι:
(α) το σημείο

ανήκει στον περιγεγραμμένο κύκλο του τριγώνου

.
(β) οι

και
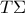
τέμνονται κάθετα στο σημείο

και ότι το

είναι το κέντρο του περιγεγραμμένου κύκλου του τριγώνου

.
3ο Θέμα
Δώδεκα φίλοι παίζουν ένα τουρνουά τένις, όπου έκαστος παίζει ένα μόνο παιγνίδι με καθέναν από τους υπόλοιπους έντεκα. Ο νικητής παίρνει ένα βαθμό. Ο ηττημένος παίρνει μηδέν βαθμούς, ενώ δεν υπάρχει ισοπαλία. Οι τελικοί βαθμοί των συμμετεχόντων είναι

. Να προσδιορίσετε τη μεγαλύτερη δυνατή τιμή του αθροίσματος

.
4ο Θέμα (επετειακό θέμα για τα 100 χρόνια της Ε.Μ.Ε.)
Να βρείτε όλους τους θετικούς ακεραίους

με

περιττό, που είναι λύσεις της εξίσωσης:

.
Αλέξανδρος
Re: ΠΡΟΚΡΙΜΑΤΙΚΟΣ 2018
Δημοσιεύτηκε: Κυρ Απρ 01, 2018 4:58 pm
από cretanman
cretanman έγραψε: ↑Κυρ Απρ 01, 2018 3:52 pm
4ο Θέμα (επετειακό θέμα για τα 100 χρόνια της Ε.Μ.Ε.)
Να βρείτε όλους τους θετικούς ακεραίους

με

περιττό, που είναι λύσεις της εξίσωσης:

Παίρνοντας

προκύπτει ότι ο

είναι περιττός. Η εξίσωση γράφεται:


Αν

τότε

. Αν τώρα ήταν

τότε

, άτοπο. Αν ήταν

τότε

, άτοπο. Επίσης

αφού ο

είναι περιττός.

Αν

τότε

απ' όπου με όμοια επιχειρήματα όπως παραπάνω προκύπτει ότι

.
(Η περίπτωση

απορρίπτεται αφού ο

είναι περιττός)
Συνεπώς η εξίσωση γίνεται

. Αν ήταν

τότε παίρνοντας

έχουμε

, άτοπο. 'Αρα

κι έτσι παίρνουμε:

. Όμως το πρώτο μέλος για

είναι μεγαλύτερο του

και το δεξί μέλος μικρότερο του

, άτοπο. Άρα

.
Έτσι, παίρνουμε μοναδική λύση την

.

: Εναλλακτικά, μόλις βγάλουμε ότι

γράφουμε την εξίσωση στη μορφή

και από το λήμμα Zsigmondy παίρνουμε εύκολα ότι

. Όμως έτσι σκοτώνουμε κουνούπι με μπαζούκα!
Αλέξανδρος
Re: ΠΡΟΚΡΙΜΑΤΙΚΟΣ 2018
Δημοσιεύτηκε: Κυρ Απρ 01, 2018 5:06 pm
από george visvikis
cretanman έγραψε: ↑Κυρ Απρ 01, 2018 3:52 pm
Καλησπέρα σε όλους!
Δίνεται οξυγώνιο τρίγωνο

με

, ο περιγεγραμμένος κύκλος του

και τα μέσα

των πλευρών

και

αντίστοιχα. Με διαμέτρους τις πλευρές

και

θεωρούμε ημικύκλια, εξωτερικά του τριγώνου, τα οποία τέμνονται από την ευθεία

στα σημεία

και

αντίστοιχα. Οι ευθείες

και
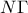
τέμνουν τον περιγεγραμμένο κύκλο στα σημεία

αντίστοιχα. Οι ευθείες

και
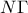
τέμνονται στο σημείο

. Να αποδείξετε ότι:
(α) το σημείο

ανήκει στον περιγεγραμμένο κύκλο του τριγώνου

.
(β) οι

και
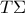
τέμνονται κάθετα στο σημείο

και ότι το

είναι το κέντρο του περιγεγραμμένου κύκλου του τριγώνου

.
Καλησπέρα!

- Προκριματικός.2018.png (25.42 KiB) Προβλήθηκε 7342 φορές
α) Επειδή

το

είναι εγγράψιμο.
β) Από την παραλληλία

και τα εγγράψιμα

είναι:

άρα το

είναι εγγράψιμο και κατά συνέπεια


οπότε

άρα το

είναι μέσο του

και το ζητούμενο έπεται.
Re: ΠΡΟΚΡΙΜΑΤΙΚΟΣ 2018
Δημοσιεύτηκε: Κυρ Απρ 01, 2018 5:26 pm
από Τσιαλας Νικολαος
Αυτή τη στιγμή βρίσκομαι εκτός. Έτσι με το μυαλό που την κοίταξα μήπως βγαίνει πολύ γρήγορα με mod9 η' μου διαφεύγει κάτι?
Re: ΠΡΟΚΡΙΜΑΤΙΚΟΣ 2018
Δημοσιεύτηκε: Κυρ Απρ 01, 2018 6:27 pm
από cretanman
Τσιαλας Νικολαος έγραψε: ↑Κυρ Απρ 01, 2018 5:26 pm
Αυτή τη στιγμή βρίσκομαι εκτός. Έτσι με το μυαλό που την κοίταξα μήπως βγαίνει πολύ γρήγορα με mod9 η' μου διαφεύγει κάτι?
Νίκο παίρνοντας

παίρνεις απλά ότι

και επειδή

και

, το μόνο που μπορείς να πάρεις είναι ότι

. Μετά δε βλέπω πως μπορείς να συνεχίσεις για να πάρεις ότι

.
Αλέξανδρος
Re: ΠΡΟΚΡΙΜΑΤΙΚΟΣ 2018
Δημοσιεύτηκε: Κυρ Απρ 01, 2018 6:31 pm
από Τσιαλας Νικολαος
Όντως!!! Μέσα σε ταβέρνα και με το μυαλό έκανα λάθος σκέψη!! Το διαπυστώσα συζητώντας με τον Σιλουανό!!


Re: ΠΡΟΚΡΙΜΑΤΙΚΟΣ 2018
Δημοσιεύτηκε: Κυρ Απρ 01, 2018 7:06 pm
από achilleas
cretanman έγραψε: ↑Κυρ Απρ 01, 2018 3:52 pm
.....
Θέματα Μικρών:
1ο Θέμα
Θεωρούμε τους θετικούς πραγματικούς αριθμούς

που είναι τέτοιοι, ώστε

. Να αποδείξετε ότι υπάρχουν δύο από τους

με άθροισμα μεγαλύτερο ή ίσο του

.
...
Μια λύση για το
1ο Θέμα:
Ας υποθέσουμε ότι

.
Εάν

, τότε τελειώσαμε, αφού θα είναι

. Αλλιώς, θα έχουμε

.
Τότε, αφού

, παίρνουμε

κι άρα

.
Έτσι, είναι

, ή ισοδύναμα

Συνεπώς,

Η απόδειξη ολοκληρώθηκε.
Φιλικά,
Αχιλλέας
Re: ΠΡΟΚΡΙΜΑΤΙΚΟΣ 2018
Δημοσιεύτηκε: Κυρ Απρ 01, 2018 10:26 pm
από ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
cretanman έγραψε: ↑Κυρ Απρ 01, 2018 3:52 pm
Καλησπέρα σε όλους!
Τα θέματα των μεγάλων
ΔΕΝ μπορούν να κοινοποιηθούν σήμερα για το λόγο ότι υπάρχουν μέσα σε αυτά θέματα από τη λίστα προβλημάτων (shortlist) διεθνών διαγωνισμών (που πρέπει να παραμείνει κρυφή μέχρι την επόμενη διοργάνωση) κι έτσι με δεδομένο ότι δεν έχει ολοκληρωθεί η διαδικασία επιλογής των ομάδων από όλες τις χώρες, τα θέματα ΔΕΝ πρέπει να γίνουν γνωστά. Αυτό έχει τονιστεί και στους διαγωνιζόμενους σήμερα.
Αλέξανδρος
Προσωπικά δεν καταλαβαίνω.
Πως θα παραμείνει κρυφή ενώ τα ξέρουν τόσα άτομα;
Δηλαδή βασιζόμαστε στην καλή πίστη των διαγωνιζομένων.
Και αν κάποιος από αυτούς τα διαρεύσει σε φίλους του στο εξωτερικό;
Μάλλον υποθέτουμε ότι δεν έχει.
Νομίζω ότι δεν είναι σοβαρά πράγματα αυτά.
Είναι προφανές ότι τα παραπάνω δεν αφορούν τον Αλέξαντρο (που πολύ καλά έκανε και το έγραψε)
αλλά αυτούς που διοργανώνουν τους διαγωνισμούς.
Re: ΠΡΟΚΡΙΜΑΤΙΚΟΣ 2018
Δημοσιεύτηκε: Κυρ Απρ 01, 2018 10:44 pm
από cretanman
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Κυρ Απρ 01, 2018 10:26 pm
Πως θα παραμείνει κρυφή ενώ τα ξέρουν τόσα άτομα;
Δηλαδή βασιζόμαστε στην καλή πίστη των διαγωνιζομένων.
Και αν κάποιος από αυτούς τα διαρεύσει σε φίλους του στο εξωτερικό;
Σταύρο επειδή η λίστα αυτή περιέχει συνήθως πολύ καλά προβλήματα από εκείνα που έχουν στείλει οι χώρες για τον εκάστοτε διαγωνισμό (είτε λέγεται BMO, είτε JBMO, είτε IMO), είναι κρίμα να πηγαίνουν χαμένα κι έτσι έχει γίνει συμφωνία μεταξύ των αρχηγών των αποστολών στους οποίους κοινοποιείται η λίστα αυτή τις μέρες του διαγωνισμού (εξάλλου από αυτή επιλέγουν τα προβλήματα του διαγωνισμού), να παραμένουν μη κοινοποιήσιμα για 1 χρόνο και μέχρι την επόμενη διοργάνωση. Ο λόγος είναι αν θέλει κάποια χώρα να χρησιμοποιήσει κάποια από αυτά τα προβλήματα να το κάνει (και το κάνουν πάρα πολλές). Μάλιστα πολλές χώρες δεν κοινοποιούν και τους διαγωνισμούς επιλογής τους ποτέ ενώ σε μας γίνεται πάντα (απλά λίγο αργότερα όταν συντρέχουν λόγοι όπως οι παραπάνω).
Πράγματι εδώ βασιζόμαστε στην καλή πίστη των διαγωνιζομένων μια και δε φαίνεται να υπάρχει καλύτερη λύση από την παραπάνω και το να μη χρησιμοποιούνται προβλήματα από αυτή μετά τη διοργάνωση του διαγωνισμού για τον οποίο προορίζονται (τότε όμως πάνε "χαμένα" τόσα όμορφα προβλήματα...). Δεν ξέρω αν υπάρχει κάτι άλλο σαν λύση!
Γενικά φαίνεται να δουλεύει μια χαρά αυτός ο τρόπος. Εξάλλου το κέρδος από αυτούς τους διαγωνισμούς είναι ένα "στεφάνι ελιάς"! Δε νομίζω να αξίζει ο κόπος να ανακατέψει κάποιος γη και ουρανό για να βρει κάποιο ή κάποια προβλήματα από shortlist προηγουμένων ετών για να γράψει καλύτερα από κάποιο άλλο και να πάρει τη θέση του σε μία διεθνή διοργάνωση στην οποία αν κάποιος δεν είναι προπονημένος, τότε είναι χαμένος από χέρι...
Αλέξανδρος
Re: ΠΡΟΚΡΙΜΑΤΙΚΟΣ 2018
Δημοσιεύτηκε: Κυρ Απρ 01, 2018 11:04 pm
από ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
cretanman έγραψε: ↑Κυρ Απρ 01, 2018 3:52 pm
1ο Θέμα
Θεωρούμε τους θετικούς πραγματικούς αριθμούς

που είναι τέτοιοι, ώστε

. Να αποδείξετε ότι υπάρχουν δύο από τους

με άθροισμα μεγαλύτερο ή ίσο του

.
Εστω

Θα έχουμε ότι

και θα θέλουμε να δείξουμε ότι

Μειώνοντας εν ανάγκη το

αρκεί να δείξουμε ότι

Θέτουμε

Εχουμε

Τα

βόσκουν πάνω σε ένα τόξο μιας έλλειψης.
Αυτό αρχίζει από το

και καταλήγει στο

Φέρουμε το ευθύγραμμο τμήμα

που σχηματίζει με τον

γωνίες

.
Εστω

σημείο του τόξου.
Φέρω την κάθετη

στον

που τέμνει το ευθύγραμμο τμήμα

στο

.
Αν

η αρχή των αξόνων τότε

Αλλά

Ετσι

και η απόδειξη ολοκληρώθηκε.
Ενα σχήμα θα βοηθούσε αλλά δεν έχω μάθει ακόμα.
Σημείωση.Υπάρχει τουλάχιστον ακόμα μια απόδειξη με τριγωνομετρία.
Re: ΠΡΟΚΡΙΜΑΤΙΚΟΣ 2018
Δημοσιεύτηκε: Κυρ Απρ 01, 2018 11:12 pm
από Τσιαλας Νικολαος
Κύριε Σταύρο αυτό όπως τόνισε ο Αλέξανδρος γίνεται παγκοσμίως!! Υπάρχουν πολλά ωραία θέματα που μπορεί να "καούν" αν δημοσιευτούν!! Αν θέλετε να δείτε μερικά από αυτά μπορείτε να ανατρέξετε στην επίσημη σελίδα της imo στην οποία θα βρείτε όλες τις shortlist μέχρι το 2016.
Re: ΠΡΟΚΡΙΜΑΤΙΚΟΣ 2018
Δημοσιεύτηκε: Δευ Απρ 02, 2018 12:01 am
από silouan
Σταύρο και Αχιλλέα, ωραίες οι προσεγγίσεις σας στο πρώτο θέμα!

Σταύρο αν θέλεις, γράψε τη λύση σου με τριγωνομετρία.
Τα πράγματα μετά τη θεώρηση της διάταξης

είναι απλά γιατί:

, οπότε

.
Re: ΠΡΟΚΡΙΜΑΤΙΚΟΣ 2018
Δημοσιεύτηκε: Δευ Απρ 02, 2018 12:37 am
από ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Κυρ Απρ 01, 2018 11:04 pm
cretanman έγραψε: ↑Κυρ Απρ 01, 2018 3:52 pm
1ο Θέμα
Θεωρούμε τους θετικούς πραγματικούς αριθμούς

που είναι τέτοιοι, ώστε

. Να αποδείξετε ότι υπάρχουν δύο από τους

με άθροισμα μεγαλύτερο ή ίσο του

.
Εστω

Θα έχουμε ότι

και θα θέλουμε να δείξουμε ότι

Μειώνοντας εν ανάγκη το

αρκεί να δείξουμε ότι

Θέτουμε

Εχουμε

Τα

βόσκουν πάνω σε ένα τόξο μιας έλλειψης.
Αυτό αρχίζει από το

και καταλήγει στο

Φέρουμε το ευθύγραμμο τμήμα

που σχηματίζει με τον

γωνίες

.
Εστω

σημείο του τόξου.
Φέρω την κάθετη

στον

που τέμνει το ευθύγραμμο τμήμα

στο

.
Αν

η αρχή των αξόνων τότε

Αλλά

Ετσι

και η απόδειξη ολοκληρώθηκε.
Ενα σχήμα θα βοηθούσε αλλά δεν έχω μάθει ακόμα.
Σημείωση.Υπάρχει τουλάχιστον ακόμα μια απόδειξη με τριγωνομετρία.
Η λύση με τριγωνομετρία.(έχει άμεση σχέση με την παραπάνω)
Εχουμε

η

θέτουμε

και θέλουμε ελαχίστη τιμή του

με την προυπόθεση ότι

λόγω της

έχουμε

λόγω της μονοτονίας του συνημιτόνου.
Re: ΠΡΟΚΡΙΜΑΤΙΚΟΣ 2018
Δημοσιεύτηκε: Δευ Απρ 02, 2018 2:26 am
από ΑΝΔΡΕΑΣ ΛΑΜΠΡΟΥ
Η λύση μου για το 1ο.(Αν υπάρχει κάποιο σφάλφμα θα παρακάλουσα να αναφερθεί).
Έστω,

και

.Από την αρχική σχέση παίρνουμε ότι:

(1) και

Όμως,

και

Άρα, από (1) έχουμε:

Άτοπο! Αφού
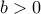
και

Άρα,

Re: ΠΡΟΚΡΙΜΑΤΙΚΟΣ 2018
Δημοσιεύτηκε: Δευ Απρ 02, 2018 8:00 am
από cretanman
ΑΝΔΡΕΑΣ ΛΑΜΠΡΟΥ έγραψε: ↑Δευ Απρ 02, 2018 2:26 am
Η λύση μου για το 1ο.(Αν υπάρχει κάποιο σφάλφμα θα παρακάλουσα να αναφερθεί).
Έστω,

και

.Από την αρχική σχέση παίρνουμε ότι:

(1) και

Όμως,

και

Άρα, από (1) έχουμε:

Άτοπο! Αφού
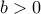
και

Άρα,

Καλημέρα Ανδρέα,
Είναι σωστή η λύση σου και ίδια με εκείνη του Αχιλλέα παραπάνω. Διαφέρουν μόνο στον τρόπο γραφής. Τα ουσιαστικά σημεία όμως δεν αλλάζουν.
Αλέξανδρος
Re: ΠΡΟΚΡΙΜΑΤΙΚΟΣ 2018
Δημοσιεύτηκε: Δευ Απρ 02, 2018 9:20 am
από achilleas
silouan έγραψε: ↑Δευ Απρ 02, 2018 12:01 am
Σταύρο και Αχιλλέα, ωραίες οι προσεγγίσεις σας στο πρώτο θέμα!

Σταύρο αν θέλεις, γράψε τη λύση σου με τριγωνομετρία.
Τα πράγματα μετά τη θεώρηση της διάταξης

είναι απλά γιατί:

, οπότε

.
Πράγματι, Σιλουανέ!

Πολύ ωραία! Επισυνάπτω και μια απόδειξη χωρίς λόγια βασισμένη στην παραπάνω απόδειξη της μιας γραμμής του Σιλουανού.
Το παρακάτω σχήμα δίνει και "δυσκολότερες" ασκήσεις. Π.χ.
Αν

και

τότε

Φιλικά,
Αχιλλέας
Re: ΠΡΟΚΡΙΜΑΤΙΚΟΣ 2018
Δημοσιεύτηκε: Δευ Απρ 02, 2018 1:39 pm
από KARKAR
Το σχήμα της ωραιότατης λύσης του Σταύρου :
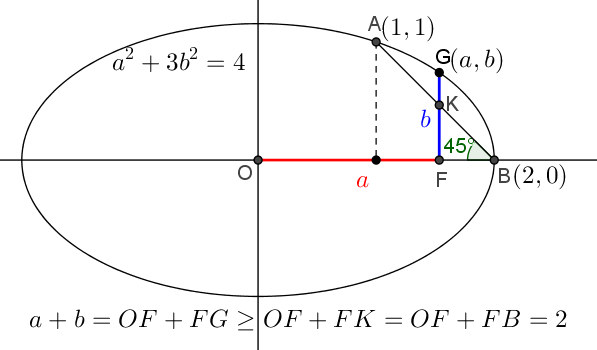
- Σταύρο-ση.png (130.6 KiB) Προβλήθηκε 6785 φορές


 που είναι τέτοιοι, ώστε
που είναι τέτοιοι, ώστε  . Να αποδείξετε ότι υπάρχουν δύο από τους
. Να αποδείξετε ότι υπάρχουν δύο από τους  με άθροισμα μεγαλύτερο ή ίσο του
με άθροισμα μεγαλύτερο ή ίσο του  .
. με
με  , ο περιγεγραμμένος κύκλος του
, ο περιγεγραμμένος κύκλος του  και τα μέσα
και τα μέσα  των πλευρών
των πλευρών  και
και  αντίστοιχα. Με διαμέτρους τις πλευρές
αντίστοιχα. Με διαμέτρους τις πλευρές  και
και  θεωρούμε ημικύκλια, εξωτερικά του τριγώνου, τα οποία τέμνονται από την ευθεία
θεωρούμε ημικύκλια, εξωτερικά του τριγώνου, τα οποία τέμνονται από την ευθεία  στα σημεία
στα σημεία  και
και  αντίστοιχα. Οι ευθείες
αντίστοιχα. Οι ευθείες  και
και  τέμνουν τον περιγεγραμμένο κύκλο στα σημεία
τέμνουν τον περιγεγραμμένο κύκλο στα σημεία  αντίστοιχα. Οι ευθείες
αντίστοιχα. Οι ευθείες  και
και  τέμνονται στο σημείο
τέμνονται στο σημείο  . Να αποδείξετε ότι:
. Να αποδείξετε ότι: ανήκει στον περιγεγραμμένο κύκλο του τριγώνου
ανήκει στον περιγεγραμμένο κύκλο του τριγώνου  .
. και
και  τέμνονται κάθετα στο σημείο
τέμνονται κάθετα στο σημείο  και ότι το
και ότι το  είναι το κέντρο του περιγεγραμμένου κύκλου του τριγώνου
είναι το κέντρο του περιγεγραμμένου κύκλου του τριγώνου  .
. . Να προσδιορίσετε τη μεγαλύτερη δυνατή τιμή του αθροίσματος
. Να προσδιορίσετε τη μεγαλύτερη δυνατή τιμή του αθροίσματος  .
. με
με  περιττό, που είναι λύσεις της εξίσωσης:
περιττό, που είναι λύσεις της εξίσωσης:  .
. προκύπτει ότι ο
προκύπτει ότι ο  είναι περιττός. Η εξίσωση γράφεται:
είναι περιττός. Η εξίσωση γράφεται: 
 Αν
Αν  τότε
τότε  . Αν τώρα ήταν
. Αν τώρα ήταν  τότε
τότε  , άτοπο. Αν ήταν
, άτοπο. Αν ήταν  τότε
τότε  , άτοπο. Επίσης
, άτοπο. Επίσης  αφού ο
αφού ο  είναι περιττός.
είναι περιττός. Αν
Αν  τότε
τότε  απ' όπου με όμοια επιχειρήματα όπως παραπάνω προκύπτει ότι
απ' όπου με όμοια επιχειρήματα όπως παραπάνω προκύπτει ότι  .
. απορρίπτεται αφού ο
απορρίπτεται αφού ο  είναι περιττός)
είναι περιττός) . Αν ήταν
. Αν ήταν  τότε παίρνοντας
τότε παίρνοντας  έχουμε
έχουμε  , άτοπο. 'Αρα
, άτοπο. 'Αρα  κι έτσι παίρνουμε:
κι έτσι παίρνουμε: . Όμως το πρώτο μέλος για
. Όμως το πρώτο μέλος για  είναι μεγαλύτερο του
είναι μεγαλύτερο του  και το δεξί μέλος μικρότερο του
και το δεξί μέλος μικρότερο του  , άτοπο. Άρα
, άτοπο. Άρα  .
. .
. : Εναλλακτικά, μόλις βγάλουμε ότι
: Εναλλακτικά, μόλις βγάλουμε ότι  γράφουμε την εξίσωση στη μορφή
γράφουμε την εξίσωση στη μορφή  και από το λήμμα Zsigmondy παίρνουμε εύκολα ότι
και από το λήμμα Zsigmondy παίρνουμε εύκολα ότι  . Όμως έτσι σκοτώνουμε κουνούπι με μπαζούκα!
. Όμως έτσι σκοτώνουμε κουνούπι με μπαζούκα!με
, ο περιγεγραμμένος κύκλος του
και τα μέσα
των πλευρών
και
αντίστοιχα. Με διαμέτρους τις πλευρές
και
θεωρούμε ημικύκλια, εξωτερικά του τριγώνου, τα οποία τέμνονται από την ευθεία
στα σημεία
και
αντίστοιχα. Οι ευθείες
και
τέμνουν τον περιγεγραμμένο κύκλο στα σημεία
αντίστοιχα. Οι ευθείες
και
τέμνονται στο σημείο
. Να αποδείξετε ότι:
ανήκει στον περιγεγραμμένο κύκλο του τριγώνου
.
και
τέμνονται κάθετα στο σημείο
και ότι το
είναι το κέντρο του περιγεγραμμένου κύκλου του τριγώνου
.
 το
το  είναι εγγράψιμο.
είναι εγγράψιμο. και τα εγγράψιμα
και τα εγγράψιμα  είναι:
είναι: 
 είναι εγγράψιμο και κατά συνέπεια
είναι εγγράψιμο και κατά συνέπεια 

 άρα το
άρα το  είναι μέσο του
είναι μέσο του  και το ζητούμενο έπεται.
και το ζητούμενο έπεται. παίρνεις απλά ότι
παίρνεις απλά ότι  και επειδή
και επειδή  και
και  , το μόνο που μπορείς να πάρεις είναι ότι
, το μόνο που μπορείς να πάρεις είναι ότι  . Μετά δε βλέπω πως μπορείς να συνεχίσεις για να πάρεις ότι
. Μετά δε βλέπω πως μπορείς να συνεχίσεις για να πάρεις ότι  .
. .
. , τότε τελειώσαμε, αφού θα είναι
, τότε τελειώσαμε, αφού θα είναι  . Αλλιώς, θα έχουμε
. Αλλιώς, θα έχουμε  .
. , παίρνουμε
, παίρνουμε  κι άρα
κι άρα .
. , ή ισοδύναμα
, ή ισοδύναμα 


 και θα θέλουμε να δείξουμε ότι
και θα θέλουμε να δείξουμε ότι 
 αρκεί να δείξουμε ότι
αρκεί να δείξουμε ότι 


 βόσκουν πάνω σε ένα τόξο μιας έλλειψης.
βόσκουν πάνω σε ένα τόξο μιας έλλειψης. και καταλήγει στο
και καταλήγει στο 
 που σχηματίζει με τον
που σχηματίζει με τον  γωνίες
γωνίες  .
. σημείο του τόξου.
σημείο του τόξου. στον
στον  που τέμνει το ευθύγραμμο τμήμα
που τέμνει το ευθύγραμμο τμήμα  στο
στο  .
. η αρχή των αξόνων τότε
η αρχή των αξόνων τότε 

 και η απόδειξη ολοκληρώθηκε.
και η απόδειξη ολοκληρώθηκε. είναι απλά γιατί:
είναι απλά γιατί: , οπότε
, οπότε  .
.και θα θέλουμε να δείξουμε ότι
αρκεί να δείξουμε ότι
βόσκουν πάνω σε ένα τόξο μιας έλλειψης.
και καταλήγει στο
που σχηματίζει με τον
γωνίες
.
σημείο του τόξου.
στον
που τέμνει το ευθύγραμμο τμήμα
στο
.
η αρχή των αξόνων τότε
και η απόδειξη ολοκληρώθηκε.
 η
η 





 και
και  .Από την αρχική σχέση παίρνουμε ότι:
.Από την αρχική σχέση παίρνουμε ότι: (1) και
(1) και  Όμως,
Όμως, και
και  Άρα, από (1) έχουμε:
Άρα, από (1) έχουμε: Άτοπο! Αφού
Άτοπο! Αφού 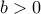 και
και 

και
.Από την αρχική σχέση παίρνουμε ότι:
(1) και
Όμως,
και
Άρα, από (1) έχουμε:
Άτοπο! Αφού
και

 και
και  τότε
τότε 