 n-οστού βαθμού ικανοποιεί τη συνθήκη
n-οστού βαθμού ικανοποιεί τη συνθήκη  για
για 
Βρείτε το
 .
.Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
 n-οστού βαθμού ικανοποιεί τη συνθήκη
n-οστού βαθμού ικανοποιεί τη συνθήκη  για
για 
 .
.H άσκηση είναι κλασική, και σίγουρα την έχουμε δει πολλές φορές στο φόρουμ. Γράφω την κύρια ιδέα:panagiotis iliopoulos έγραψε: ↑Σάβ Μαρ 24, 2018 8:35 pmΈνα πολυώνυμοn-οστού βαθμού ικανοποιεί τη συνθήκη
για

Βρείτε το.

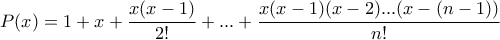
 για
για  . Ως βαθμού
. Ως βαθμού  είναι μοναδικό. Και λοιπά.
είναι μοναδικό. Και λοιπά.panagiotis iliopoulos έγραψε: ↑Σάβ Μαρ 24, 2018 8:35 pmΈνα πολυώνυμοn-οστού βαθμού ικανοποιεί τη συνθήκη
για

Βρείτε το.
 καθορίζεται πλήρως από
καθορίζεται πλήρως από  τιμές του και μάλιστα από το θεώρημα παρεμβολής του Lagrange έχουμε και τύπο. Άμα το χρησιμοποιήσουμε στο πρόβλημα μας παίρνουμε
τιμές του και μάλιστα από το θεώρημα παρεμβολής του Lagrange έχουμε και τύπο. Άμα το χρησιμοποιήσουμε στο πρόβλημα μας παίρνουμε 
 . Έχουμε
. Έχουμε
 για να απλοποιήσουμε το άθροισμα με το διωνυμικό θεώρημα.
για να απλοποιήσουμε το άθροισμα με το διωνυμικό θεώρημα.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης