Soteris έγραψε: ↑Σάβ Μαρ 24, 2018 1:07 pm
Πρόβλημα 4
Έστω

ένα σύνολο

διαδοχικών θετικών ακεραίων και

μία μετάθεση των στοιχείων του

.
(α) Να αποδείξετε ότι:

(β) Να βρείτε τον μεγαλύτερο θετικό ακέραιο

, έτσι ώστε το

τετράγωνο να μπορεί να χωριστεί σε

ορθογώνια που ανά δύο να μην έχουν κοινά εσωτερικά σημεία και τα μήκη και πλάτη τους να σχηματίζουν την ακολουθία

.
Όμορφο πρόβλημα!
(α) Θα κάνω την απόδειξη με ισχυρή επαγωγή στο ήμισυ του πλήθους των στοιχείων του

. Για ευκολία θα συμβολίζω με

το
![\displaystyle\sum_{i=1}^{k}\left[(2i-1)2i\right] \displaystyle\sum_{i=1}^{k}\left[(2i-1)2i\right]](/forum/ext/geomar/texintegr/latexrender/pictures/ab3fe132c3405ac012af2c4c98d76424.png)
.
Για

δηλαδή με

ο ισχυρισμός προφανώς ισχύει (δοκιμάζουμε όλους τους πιθανούς συνδυασμούς και όλοι είναι μικρότεροι του

)
Ας υποθέσουμε τώρα ότι ο ισχυρισμός ισχύει όταν

με

. Τότε για οποιαδήποτε μετάθεση

των στοιχείων του

θα ισχύει ότι

Θα κάνουμε την απόδειξη όταν

δηλαδή

αποδεικνύοντας ότι για οποιαδήποτε μετάθεση

των στοιχείων του

ισχύει

Διακρίνουμε τις εξής περιπτώσεις:

Κάποιο εκ των γινομένων

που εμφανίζονται στο παραπάνω άθροισμα, ας υποθέσουμε χωρίς βλάβη της γενικότητας το

, είναι ίσο με

. Τότε

και η απόδειξη ολοκληρώθηκε.

Κάποιο

είναι ίσο με

, ας υποθέσουμε

και κάποιο

ίσο με

, ας υποθέσουμε

και τα

δεν εμφανίζονται στο ίδιο γινόμενο. Τότε έχουμε διαδοχικά:

και η απόδειξη ολοκληρώθηκε.
(β) To άθροισμα των εμβαδών των ορθογωνίων είναι ίσο με

όπου

μία μετάθεση των

και από την άλλη πρέπει να είναι ίσο με το εμβαδό του τετραγώνου δηλαδή

.
Συνεπώς από το (α) ερώτημα έχουμε
![m^2= \displaystyle\sum_{i=1}^{7}a_{2i-1}a_{2i} \leq \displaystyle\sum_{i=1}^{k}\left[(2i-1)2i\right]=504 m^2= \displaystyle\sum_{i=1}^{7}a_{2i-1}a_{2i} \leq \displaystyle\sum_{i=1}^{k}\left[(2i-1)2i\right]=504](/forum/ext/geomar/texintegr/latexrender/pictures/9690b995f782d2917159c09764526cbe.png)
Άρα

κι επειδή

άρα

. Μένει να κατασκευάσουμε ένα τετράγωνο διαστάσεων

που να χωρίζεται σε

ορθογώνια όπως ορίζει η εκφώνηση. Η κατασκευή φαίνεται παρακάτω κι έτσι η μέγιστη τιμή του
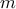
είναι το
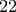
.

- CYP_3rdTST_2018.png (14.49 KiB) Προβλήθηκε 1208 φορές
Αλέξανδρος
 , για τους οποίους ο αριθμός
, για τους οποίους ο αριθμός  (ο αριθμός με βάση το
(ο αριθμός με βάση το  ) είναι τέλειο τετράγωνο.
) είναι τέλειο τετράγωνο. με
με  και
και  . Αν
. Αν  το μέσον της πλευράς
το μέσον της πλευράς  και
και  τα περίκεντρα των τριγώνων
τα περίκεντρα των τριγώνων  , αντίστοιχα, να αποδείξετε ότι το εμβαδόν του τραπεζίου
, αντίστοιχα, να αποδείξετε ότι το εμβαδόν του τραπεζίου  είναι εξαπλάσιο από το εμβαδόν του τριγώνου
είναι εξαπλάσιο από το εμβαδόν του τριγώνου  .
. είναι θετικοί πραγματικοί αριθμοί, να βρείτε όλες τις τριάδες
είναι θετικοί πραγματικοί αριθμοί, να βρείτε όλες τις τριάδες  , για τις οποίες η παράσταση
, για τις οποίες η παράσταση  παίρνει την ελάχιστη τιμή της.
παίρνει την ελάχιστη τιμή της.  ένα σύνολο
ένα σύνολο  διαδοχικών θετικών ακεραίων και
διαδοχικών θετικών ακεραίων και  μία μετάθεση των στοιχείων του
μία μετάθεση των στοιχείων του  .
.
 , έτσι ώστε το
, έτσι ώστε το  τετράγωνο να μπορεί να χωριστεί σε
τετράγωνο να μπορεί να χωριστεί σε  ορθογώνια που ανά δύο να μην έχουν κοινά εσωτερικά σημεία και τα μήκη και πλάτη τους να σχηματίζουν την ακολουθία
ορθογώνια που ανά δύο να μην έχουν κοινά εσωτερικά σημεία και τα μήκη και πλάτη τους να σχηματίζουν την ακολουθία  .
.
 , με
, με  θετικοί ακέραιοι.
θετικοί ακέραιοι.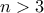 .
. άρτιος τότε παρατηρούμε πως:
άρτιος τότε παρατηρούμε πως:

 είναι ανάμεσα σε δύο διαδοχικά τέλεια τετράγωνο, άτοπο.
είναι ανάμεσα σε δύο διαδοχικά τέλεια τετράγωνο, άτοπο.
 , καθώς για
, καθώς για 
 και
και  δίνουν
δίνουν  (άτοπο) και
(άτοπο) και  (εγκρίνεται). Άρα μοναδική περίπτωση είναι
(εγκρίνεται). Άρα μοναδική περίπτωση είναι 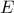 είναι το μέσο του
είναι το μέσο του  θα είναι
θα είναι  Αρκεί να δείξω λοιπόν ότι:
Αρκεί να δείξω λοιπόν ότι: 
 οι ακτίνες των κύκλων
οι ακτίνες των κύκλων  Τότε λόγω των γωνιών των
Τότε λόγω των γωνιών των  θα είναι
θα είναι 
 θα είναι:
θα είναι: 



 .
.
 . Για ευκολία θα συμβολίζω με
. Για ευκολία θα συμβολίζω με  το
το ![\displaystyle\sum_{i=1}^{k}\left[(2i-1)2i\right] \displaystyle\sum_{i=1}^{k}\left[(2i-1)2i\right]](/forum/ext/geomar/texintegr/latexrender/pictures/ab3fe132c3405ac012af2c4c98d76424.png) .
. δηλαδή με
δηλαδή με  ο ισχυρισμός προφανώς ισχύει (δοκιμάζουμε όλους τους πιθανούς συνδυασμούς και όλοι είναι μικρότεροι του
ο ισχυρισμός προφανώς ισχύει (δοκιμάζουμε όλους τους πιθανούς συνδυασμούς και όλοι είναι μικρότεροι του  )
) με
με  . Τότε για οποιαδήποτε μετάθεση
. Τότε για οποιαδήποτε μετάθεση  των στοιχείων του
των στοιχείων του 
 δηλαδή
δηλαδή  αποδεικνύοντας ότι για οποιαδήποτε μετάθεση
αποδεικνύοντας ότι για οποιαδήποτε μετάθεση 
 Κάποιο εκ των γινομένων
Κάποιο εκ των γινομένων  που εμφανίζονται στο παραπάνω άθροισμα, ας υποθέσουμε χωρίς βλάβη της γενικότητας το
που εμφανίζονται στο παραπάνω άθροισμα, ας υποθέσουμε χωρίς βλάβη της γενικότητας το  , είναι ίσο με
, είναι ίσο με  . Τότε
. Τότε  και η απόδειξη ολοκληρώθηκε.
και η απόδειξη ολοκληρώθηκε. , ας υποθέσουμε
, ας υποθέσουμε  και κάποιο
και κάποιο  ίσο με
ίσο με  , ας υποθέσουμε
, ας υποθέσουμε  και τα
και τα  δεν εμφανίζονται στο ίδιο γινόμενο. Τότε έχουμε διαδοχικά:
δεν εμφανίζονται στο ίδιο γινόμενο. Τότε έχουμε διαδοχικά:
 όπου
όπου  μία μετάθεση των
μία μετάθεση των  και από την άλλη πρέπει να είναι ίσο με το εμβαδό του τετραγώνου δηλαδή
και από την άλλη πρέπει να είναι ίσο με το εμβαδό του τετραγώνου δηλαδή ![m^2= \displaystyle\sum_{i=1}^{7}a_{2i-1}a_{2i} \leq \displaystyle\sum_{i=1}^{k}\left[(2i-1)2i\right]=504 m^2= \displaystyle\sum_{i=1}^{7}a_{2i-1}a_{2i} \leq \displaystyle\sum_{i=1}^{k}\left[(2i-1)2i\right]=504](/forum/ext/geomar/texintegr/latexrender/pictures/9690b995f782d2917159c09764526cbe.png)
 κι επειδή
κι επειδή  άρα
άρα  . Μένει να κατασκευάσουμε ένα τετράγωνο διαστάσεων
. Μένει να κατασκευάσουμε ένα τετράγωνο διαστάσεων  που να χωρίζεται σε
που να χωρίζεται σε  ορθογώνια όπως ορίζει η εκφώνηση. Η κατασκευή φαίνεται παρακάτω κι έτσι η μέγιστη τιμή του
ορθογώνια όπως ορίζει η εκφώνηση. Η κατασκευή φαίνεται παρακάτω κι έτσι η μέγιστη τιμή του 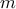 είναι το
είναι το 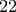 .
.