Πρώτη Μέρα.
Πρόβλημα 1. Το δευτεροβάθμιο τριώνυμο
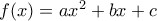 παίρνει ετερόσημες τιμές στα σημεία
παίρνει ετερόσημες τιμές στα σημεία  και
και  . Αποδείξτε, ότι οι ρίζες του τριωνύμου
. Αποδείξτε, ότι οι ρίζες του τριωνύμου  έχουν ετερόσημες τιμές.
έχουν ετερόσημες τιμές.Πρόβλημα 2. Να βρείτε όλες τις τιμές του
 , για τις οποίες θα βρεθούν τέτοια
, για τις οποίες θα βρεθούν τέτοια  και
και  , ώστε οι αριθμοί
, ώστε οι αριθμοί 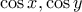 και
και 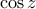 να είναι ανά δυο διαφορετικοί μεταξύ τους και να σχηματίζουν αριθμητική πρόοδο με τη δοθείσα σειρά, επιπλέον οι αριθμοί
να είναι ανά δυο διαφορετικοί μεταξύ τους και να σχηματίζουν αριθμητική πρόοδο με τη δοθείσα σειρά, επιπλέον οι αριθμοί 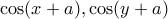 και
και  επίσης να αποτελούν αριθμητική πρόοδο με την δοθείσα σειρά.
επίσης να αποτελούν αριθμητική πρόοδο με την δοθείσα σειρά.Πρόβλημα 3. Στις πλευρές
 και
και  παραλληλογράμμου
παραλληλογράμμου  με κέντρο
με κέντρο  σημειώθηκαν σημεία
σημειώθηκαν σημεία  και
και  αντίστοιχα, ώστε
αντίστοιχα, ώστε 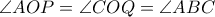 .
. α) Αποδείξτε, ότι
 .
.β) Αποδείξτε, ότι οι ευθείες
 και
και  τέμνονται στον περιγεγραμμένο κύκλο του τριγώνου
τέμνονται στον περιγεγραμμένο κύκλο του τριγώνου 
Πρόβλημα 4. Ο Αλέξανδρος παρατήρησε, ότι στο πληκτρολόγιο του έμειναν
 λειτουργικά πλήκτρα με ψηφία. Προέκυψε, ότι οποιοδήποτε φυσικός αριθμός από το
λειτουργικά πλήκτρα με ψηφία. Προέκυψε, ότι οποιοδήποτε φυσικός αριθμός από το  μέχρι το
μέχρι το 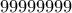 μπορεί να σχηματιστεί, είτε πληκτρολογώντας τα λειτουργικά πλήκτρα, είτε ως αποτέλεσμα αθροίσματος δυο φυσικών αριθμών, καθένας εκ των οποίων μπορεί να πληκτρολογηθεί, χρησιμοποιώντας τα πλήκτρα που λειτουργούν. Για ποιο ελάχιστο
μπορεί να σχηματιστεί, είτε πληκτρολογώντας τα λειτουργικά πλήκτρα, είτε ως αποτέλεσμα αθροίσματος δυο φυσικών αριθμών, καθένας εκ των οποίων μπορεί να πληκτρολογηθεί, χρησιμοποιώντας τα πλήκτρα που λειτουργούν. Για ποιο ελάχιστο  , αυτό είναι δυνατό;
, αυτό είναι δυνατό;Πρόβλημα 5. Το πολυώνυμο
 ικανοποιεί τις ακόλουθες σχέσεις:
ικανοποιεί τις ακόλουθες σχέσεις: 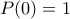 ,
, 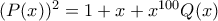 για όλα τα πραγματικά
για όλα τα πραγματικά  , όπου
, όπου  κάποιο πολυώνυμο. Να αποδείξετε, ότι ο συντελεστής του
κάποιο πολυώνυμο. Να αποδείξετε, ότι ο συντελεστής του  του πολυωνύμου
του πολυωνύμου 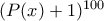 είναι ίσος με μηδέν.
είναι ίσος με μηδέν.Πρόβλημα 6. Σε ένα βασίλειο μερικά ζεύγη πόλεων είναι συνδεδεμένα με σιδηροδρομική γραμμή. Ο βασιλιάς έχει μια πλήρη λίστα, στην οποία είναι απαριθμημένα κατά όνομα όλα τα τέτοια ζεύγη (κάθε πόλη έχει το δικό της προσωπικό όνομα). Προέκυψε, ότι για οποιοδήποτε διατεταγμένο ζεύγος πόλεων ο πρίγκιπας μπορεί να μετονομάσει όλες τις πόλεις έτσι, ώστε η πρώτη πόλη να καταλήξει να έχει το όνομα της δεύτερης πόλης και ο βασιλιάς να μην αντιληφθεί την αλλαγή. Είναι άραγε αληθές, ότι για οποιοδήποτε ζεύγος ο πρίγκιπας μπορεί να μετονομάσει όλες τις πόλεις έτσι, ώστε η πρώτη πόλη να καταλήξει να έχει το όνομα της δεύτερης πόλης, η δεύτερη πόλη να καταλήξει να έχει το όνομα της πρώτης και ο βασιλιάς να μην αντιληφθεί την αλλαγή;
Δεύτερη Μέρα.
Πρόβλημα 1. Υπάρχει άραγε δευτεροβάθμιο τριώνυμο
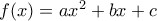 με ακέραιους συντελεστές και
με ακέραιους συντελεστές και  να μην διαιρείται με το
να μην διαιρείται με το  , ώστε όλοι οι αριθμοί
, ώστε όλοι οι αριθμοί 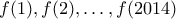 να αφήνουν διαφορετικά υπόλοιπα με την διαίρεσή τους με το
να αφήνουν διαφορετικά υπόλοιπα με την διαίρεσή τους με το  ; Εξηγήστε τη απάντηση.
; Εξηγήστε τη απάντηση.Πρόβλημα 2. Να βρείτε όλα τα
 και
και  τέτοια ώστε
τέτοια ώστε 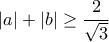 και για όλα τα
και για όλα τα  να ικανοποιείται η ανισότητα
να ικανοποιείται η ανισότητα 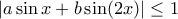 .
.Πρόβλημα 3. Να αποδείξετε, ότι για οποιοδήποτε φυσικό
 θα βρεθεί φυσικός αριθμός, η δεκαδική αναπαράσταση του τετραγώνου του οποίου αρχίζει με
θα βρεθεί φυσικός αριθμός, η δεκαδική αναπαράσταση του τετραγώνου του οποίου αρχίζει με  μονάδες και τελειώνει με κάποιο συνδυασμό
μονάδες και τελειώνει με κάποιο συνδυασμό  δυάρια και μονάδες.
δυάρια και μονάδες.Πρόβλημα 4. Ένας σεφ έχει υπό την επίβλεψή του δέκα μάγειρες, μερικοί από τους οποίους έχουν φιλία μεταξύ τους. Κάθε εργάσιμη μέρα ο σεφ αναθέτει έναν ή μερικούς μάγειρες σε επιμελητές καθαριότητας, ο καθένας εκ των επιμελητών φεύγοντας από την δουλειά παίρνει μαζί του από ένα γλυκό σε κάθε μη επιμελητή φίλο του. Στο τέλος της μέρας ο σεφ γνωρίζει πόσα γλυκά λείπουν. Μπορεί άραγε σε
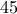 εργάσιμες μέρες να καταλάβει, ποιοι εκ των μαγείρων είναι φίλοι μεταξύ τους, και ποιοι όχι;
εργάσιμες μέρες να καταλάβει, ποιοι εκ των μαγείρων είναι φίλοι μεταξύ τους, και ποιοι όχι;Πρόβλημα 5. Η επιφάνεια του κυρτού πολύεδρου
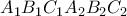 αποτελείται από οχτώ τριγωνικές έδρες
αποτελείται από οχτώ τριγωνικές έδρες 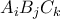 όπου τα
όπου τα  παίρνουν τιμές από
παίρνουν τιμές από  έως
έως  . Σφαίρα με κέντρο το σημείο
. Σφαίρα με κέντρο το σημείο  εφάπτεται όλων αυτών των εδρών. Να αποδείξετε ότι το σημείο
εφάπτεται όλων αυτών των εδρών. Να αποδείξετε ότι το σημείο  και τα μέσα των τριών τμημάτων
και τα μέσα των τριών τμημάτων 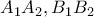 και
και 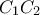 βρίσκονται στο ίδιο επίπεδο.
βρίσκονται στο ίδιο επίπεδο.
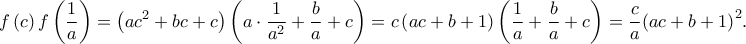
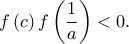 Άρα, θα είναι
Άρα, θα είναι  οπότε (από τον τύπο του Vieta) το δευτεροβάθμιο τριώνυμο
οπότε (από τον τύπο του Vieta) το δευτεροβάθμιο τριώνυμο  έχει ετερόσημες ρίζες.
έχει ετερόσημες ρίζες.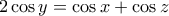

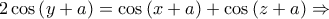
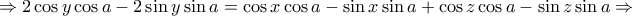
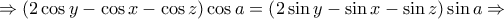
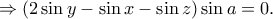
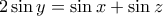
 .
.
 και
και 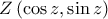 του μοναδιαίου κύκλου. Τότε, από τις σχέσεις
του μοναδιαίου κύκλου. Τότε, από τις σχέσεις  είναι το μέσο του ευθύγραμμου τμήματος
είναι το μέσο του ευθύγραμμου τμήματος  , πράγμα άτοπο.
, πράγμα άτοπο. 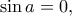 οπότε
οπότε 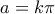 με
με  .
.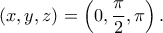
 είναι ρίζα του πολυωνύμου
είναι ρίζα του πολυωνύμου 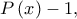 θα υπάρχει πολυώνυμο
θα υπάρχει πολυώνυμο  τέτοιο, ώστε
τέτοιο, ώστε 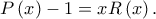
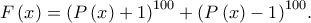

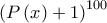 είναι ίσος με το συντελεστή του
είναι ίσος με το συντελεστή του 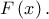


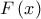 είναι ίσος με
είναι ίσος με 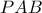 και
και 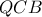 είναι όμοια. Αφού
είναι όμοια. Αφού 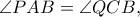 αρκεί να αποδείξουμε ότι
αρκεί να αποδείξουμε ότι 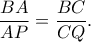
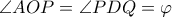 και
και 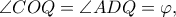 τα τετράπλευρα
τα τετράπλευρα  και
και  είναι εγγράψιμα σε κύκλο. Συνεπώς:
είναι εγγράψιμα σε κύκλο. Συνεπώς: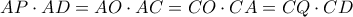

 το σημείο τομής των
το σημείο τομής των 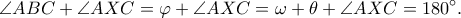
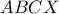 είναι εγγράψιμο σε κύκλο και το ζητούμενο δείχθηκε.
είναι εγγράψιμο σε κύκλο και το ζητούμενο δείχθηκε.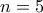 γίνεται με τα ψηφία
γίνεται με τα ψηφία  . Αυτό είναι άμεσο επειδή κάθε αριθμός από το
. Αυτό είναι άμεσο επειδή κάθε αριθμός από το  μπορεί να γραφτεί ως άθροισμα δύο εκ των ψηφίων. Άρα μπορούμε να σχηματίσουμε και κάθε φυσικό αριθμό ως άθροισμα δύο πληκτρολογίσιμων φυσικών αριθμών κάνοντας την επιλογή ψηφίο προς ψηφίο χωρίς να χρειαστεί κράτημα.
μπορεί να γραφτεί ως άθροισμα δύο εκ των ψηφίων. Άρα μπορούμε να σχηματίσουμε και κάθε φυσικό αριθμό ως άθροισμα δύο πληκτρολογίσιμων φυσικών αριθμών κάνοντας την επιλογή ψηφίο προς ψηφίο χωρίς να χρειαστεί κράτημα. . Πράγματι κοιτάζοντας τα τελικά ψηφία μόνα τους, μπορούμε να πάρουμε το πολύ
. Πράγματι κοιτάζοντας τα τελικά ψηφία μόνα τους, μπορούμε να πάρουμε το πολύ 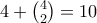 τελικά ψηφία. Η ισότητα θα ισχύει αν κάθε δύο ψηφία που προσθέτουμε έχουν διαφορετικό τελικό ψηφίο το οποίο να είναι μάλιστα διαφορετικό από τα ψηφία που έχουμε.
τελικά ψηφία. Η ισότητα θα ισχύει αν κάθε δύο ψηφία που προσθέτουμε έχουν διαφορετικό τελικό ψηφίο το οποίο να είναι μάλιστα διαφορετικό από τα ψηφία που έχουμε.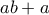 περιττά ψηφία. Θέλουμε όμως
περιττά ψηφία. Θέλουμε όμως  περιττά ψηφία και πρέπει να έχουμε ισότητα. (Αλλιώς θα έχουμε λιγότερα άρτια ψηφία.) Όμως η εξίσωση
περιττά ψηφία και πρέπει να έχουμε ισότητα. (Αλλιώς θα έχουμε λιγότερα άρτια ψηφία.) Όμως η εξίσωση 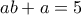 δίνει
δίνει 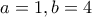 , ή
, ή  , άτοπο αφού
, άτοπο αφού 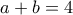 .
. μέρες, αφήνει τους μάγειρες
μέρες, αφήνει τους μάγειρες  έχει
έχει  φίλους και ο
φίλους και ο  έχει
έχει  φίλους, όταν τους αφήσει μαζί, είτε θα είναι φίλοι και θα λείπουν
φίλους, όταν τους αφήσει μαζί, είτε θα είναι φίλοι και θα λείπουν  γλυκά, είτε δεν θα είναι φίλοι και θα λείπουν
γλυκά, είτε δεν θα είναι φίλοι και θα λείπουν  γλυκά.
γλυκά. ![\displaystyle \begin{tikzpicture}[line cap=round,line join=round,>=triangle 45,x=1.0cm,y=1.0cm]
\clip(9.58053539513193,1.1797463385788545) rectangle (16.582110139968258,7.479098247649878);
\draw [line width=0.8pt] (10.585786437626904,5.414213562373096)-- (12.,6.82842712474619);
\draw [line width=0.8pt] (12.,6.82842712474619)-- (12.51763809020504,4.8965754721680534);
\draw [line width=0.8pt] (12.51763809020504,4.8965754721680534)-- (10.585786437626904,5.414213562373096);
\draw [line width=0.8pt] (13.482361909794959,4.896575472168053)-- (14.,6.82842712474619);
\draw [line width=0.8pt] (14.,6.82842712474619)-- (15.414213562373096,5.414213562373095);
\draw [line width=0.8pt] (15.414213562373096,5.414213562373095)-- (13.482361909794959,4.896575472168053);
\draw [line width=0.8pt] (10.585786437626904,3.414213562373096)-- (12.517638090205041,3.9318516525781373);
\draw [line width=0.8pt] (12.517638090205041,3.9318516525781373)-- (12.,2.);
\draw [line width=0.8pt] (12.,2.)-- (10.585786437626904,3.414213562373096);
\draw [line width=0.8pt] (13.482361909794959,3.9318516525781373)-- (14.,2.);
\draw [line width=0.8pt] (14.,2.)-- (15.414213562373096,3.414213562373095);
\draw [line width=0.8pt] (15.414213562373096,3.414213562373095)-- (13.482361909794959,3.9318516525781373);
\draw [line width=0.8pt] (10.585786437626904,3.414213562373096)-- (10.585786437626904,5.414213562373096);
\draw [line width=0.8pt] (12.,6.82842712474619)-- (14.,6.82842712474619);
\draw [line width=0.8pt] (15.414213562373096,5.414213562373095)-- (15.414213562373096,3.414213562373095);
\draw [line width=0.8pt] (14.,2.)-- (12.,2.);
\draw [line width=0.8pt] (12.517638090205041,3.9318516525781373)-- (13.482361909794959,4.896575472168053);
\draw [line width=0.8pt] (13.482361909794959,3.9318516525781373)-- (12.51763809020504,4.8965754721680534);
\draw (11.7,7.2312548938503625) node[anchor=north west] {1};
\draw (14.062369376339845,7.251908506666989) node[anchor=north west] {2};
\draw (15.570083111953567,5.599619481336884) node[anchor=north west] {3};
\draw (15.570083111953567,3.430990135591122) node[anchor=north west] {4};
\draw (13.979754925073339,1.8406619487108964) node[anchor=north west] {5};
\draw (11.76981835369432,1.8406619487108964) node[anchor=north west] {6};
\draw (10.220797392447347,3.348375684324617) node[anchor=north west] {7};
\draw (10.179490166814094,5.661580319786763) node[anchor=north west] {8};
\draw (13.5,5.5) node[anchor=north west] {9};
\draw (13.58733628155744,3.761447940657143) node[anchor=north west] {10};
\draw (11.6,3.699487102207264) node[anchor=north west] {11};
\draw (11.955700869043959,5.3724297403539945) node[anchor=north west] {12};
\draw [fill=white] (12.,2.) circle (1.5pt);
\draw [fill=white] (14.,2.) circle (1.5pt);
\draw [fill=white] (15.414213562373096,3.414213562373095) circle (1.5pt);
\draw [fill=white] (15.414213562373096,5.414213562373095) circle (1.5pt);
\draw [fill=white] (14.,6.82842712474619) circle (1.5pt);
\draw [fill=white] (12.,6.82842712474619) circle (1.5pt);
\draw [fill=white] (10.585786437626904,5.414213562373096) circle (1.5pt);
\draw [fill=white] (10.585786437626904,3.414213562373096) circle (1.5pt);
\draw [fill=white] (12.517638090205041,3.9318516525781373) circle (1.5pt);
\draw [fill= white] (13.482361909794959,3.9318516525781373) circle (1.5pt);
\draw [fill= white] (13.482361909794959,4.896575472168053) circle (1.5pt);
\draw [fill= white] (12.51763809020504,4.8965754721680534) circle (1.5pt);
\end{tikzpicture} \displaystyle \begin{tikzpicture}[line cap=round,line join=round,>=triangle 45,x=1.0cm,y=1.0cm]
\clip(9.58053539513193,1.1797463385788545) rectangle (16.582110139968258,7.479098247649878);
\draw [line width=0.8pt] (10.585786437626904,5.414213562373096)-- (12.,6.82842712474619);
\draw [line width=0.8pt] (12.,6.82842712474619)-- (12.51763809020504,4.8965754721680534);
\draw [line width=0.8pt] (12.51763809020504,4.8965754721680534)-- (10.585786437626904,5.414213562373096);
\draw [line width=0.8pt] (13.482361909794959,4.896575472168053)-- (14.,6.82842712474619);
\draw [line width=0.8pt] (14.,6.82842712474619)-- (15.414213562373096,5.414213562373095);
\draw [line width=0.8pt] (15.414213562373096,5.414213562373095)-- (13.482361909794959,4.896575472168053);
\draw [line width=0.8pt] (10.585786437626904,3.414213562373096)-- (12.517638090205041,3.9318516525781373);
\draw [line width=0.8pt] (12.517638090205041,3.9318516525781373)-- (12.,2.);
\draw [line width=0.8pt] (12.,2.)-- (10.585786437626904,3.414213562373096);
\draw [line width=0.8pt] (13.482361909794959,3.9318516525781373)-- (14.,2.);
\draw [line width=0.8pt] (14.,2.)-- (15.414213562373096,3.414213562373095);
\draw [line width=0.8pt] (15.414213562373096,3.414213562373095)-- (13.482361909794959,3.9318516525781373);
\draw [line width=0.8pt] (10.585786437626904,3.414213562373096)-- (10.585786437626904,5.414213562373096);
\draw [line width=0.8pt] (12.,6.82842712474619)-- (14.,6.82842712474619);
\draw [line width=0.8pt] (15.414213562373096,5.414213562373095)-- (15.414213562373096,3.414213562373095);
\draw [line width=0.8pt] (14.,2.)-- (12.,2.);
\draw [line width=0.8pt] (12.517638090205041,3.9318516525781373)-- (13.482361909794959,4.896575472168053);
\draw [line width=0.8pt] (13.482361909794959,3.9318516525781373)-- (12.51763809020504,4.8965754721680534);
\draw (11.7,7.2312548938503625) node[anchor=north west] {1};
\draw (14.062369376339845,7.251908506666989) node[anchor=north west] {2};
\draw (15.570083111953567,5.599619481336884) node[anchor=north west] {3};
\draw (15.570083111953567,3.430990135591122) node[anchor=north west] {4};
\draw (13.979754925073339,1.8406619487108964) node[anchor=north west] {5};
\draw (11.76981835369432,1.8406619487108964) node[anchor=north west] {6};
\draw (10.220797392447347,3.348375684324617) node[anchor=north west] {7};
\draw (10.179490166814094,5.661580319786763) node[anchor=north west] {8};
\draw (13.5,5.5) node[anchor=north west] {9};
\draw (13.58733628155744,3.761447940657143) node[anchor=north west] {10};
\draw (11.6,3.699487102207264) node[anchor=north west] {11};
\draw (11.955700869043959,5.3724297403539945) node[anchor=north west] {12};
\draw [fill=white] (12.,2.) circle (1.5pt);
\draw [fill=white] (14.,2.) circle (1.5pt);
\draw [fill=white] (15.414213562373096,3.414213562373095) circle (1.5pt);
\draw [fill=white] (15.414213562373096,5.414213562373095) circle (1.5pt);
\draw [fill=white] (14.,6.82842712474619) circle (1.5pt);
\draw [fill=white] (12.,6.82842712474619) circle (1.5pt);
\draw [fill=white] (10.585786437626904,5.414213562373096) circle (1.5pt);
\draw [fill=white] (10.585786437626904,3.414213562373096) circle (1.5pt);
\draw [fill=white] (12.517638090205041,3.9318516525781373) circle (1.5pt);
\draw [fill= white] (13.482361909794959,3.9318516525781373) circle (1.5pt);
\draw [fill= white] (13.482361909794959,4.896575472168053) circle (1.5pt);
\draw [fill= white] (12.51763809020504,4.8965754721680534) circle (1.5pt);
\end{tikzpicture}](/forum/ext/geomar/texintegr/latexrender/pictures/e8ccf90262cd6d29ce09131d920b6361.png)
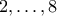 χωρίς ο βασιλιάς να το πάρει είδηση. Μπορούμε να αλλάξουμε επίσης το όνομα της πόλης
χωρίς ο βασιλιάς να το πάρει είδηση. Μπορούμε να αλλάξουμε επίσης το όνομα της πόλης  (και άρα και σε
(και άρα και σε 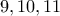 ) χωρίς πάλι ο βασιλιάς να το πάρει είδηση. Αρκεί να ονομάσουμε τις πόλεις
) χωρίς πάλι ο βασιλιάς να το πάρει είδηση. Αρκεί να ονομάσουμε τις πόλεις 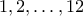 ως εξής:
ως εξής: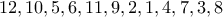
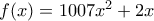
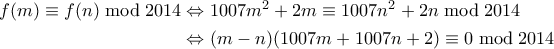
 αφήνουν το ίδιο υπόλοιπο, τότε πρέπει
αφήνουν το ίδιο υπόλοιπο, τότε πρέπει 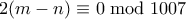 και
και 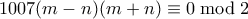 . Η πρώτη δίνει ότι
. Η πρώτη δίνει ότι  και η δεύτερη ότι
και η δεύτερη ότι  . Αλλά τότε
. Αλλά τότε  .
. 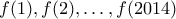 αφήνουν όλοι διαφορετικά υπόλοιπα.
αφήνουν όλοι διαφορετικά υπόλοιπα.
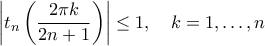 .
. 
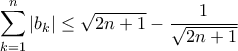 .
.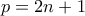 είναι πρώτος και
είναι πρώτος και 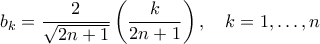 .
.
 και τις ανισότητες
και τις ανισότητες  . Τότε
. Τότε .
. .
. είναι το σύμβολο του Legendre. Για
είναι το σύμβολο του Legendre. Για 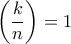 , αν ο
, αν ο  είναι ίσος με το υπόλοιπο της διαίρεσης ενός τετραγώνου φυσικού αριθμού με τον
είναι ίσος με το υπόλοιπο της διαίρεσης ενός τετραγώνου φυσικού αριθμού με τον 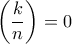 , αν ο
, αν ο 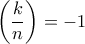 στις υπόλοιπες περιπτώσεις.
στις υπόλοιπες περιπτώσεις.