ΕΥΚΛΕΙΔΗΣ 2017 - 2018

#61

melasjumper έγραψε: ↑
Σάβ Ιαν 20, 2018 1:30 pm
ΘΕΜΑ 2 Γ ΛΥΚΕΙΟΥ
Θα αποδείξουμε κατι περισσότερο.Εστω
$g(x)=a_1\cos(r_1x+b_1)+\cdots+a_n\cos(r_nx+b_n)$
Αν τα είναι ανα δύο διαφορετικα και η ειναι περιοδική με περίοδο Τ τοτε ολοι οι οροι $\cos(r_ix+b_i)$
ειναι περιοδικοι με περιοδο Τ.

Παραγωγίζουμε την φορες για k=0,1,2,...,n-1.Αυτοι οι παραγωγοι ειναι περιοδικοι με περιοδο Τ.
Aυτο που βγαινει ειναι $g^{(2k)}(x)=a_1r^{2k}_1\cos(r_1x+b_1)+\cdots+a_nr^{2k}_n\cos(r_nx+b_n)$ χωρις τα προσημα.Καθε γραμμικος
συνδυασμος αυτων ειναι περιοδικος με περιοδο Τ.Θελουμε για να φτιαξουμε τους ορους $\cos(r_ix+b_i)$ ετσι ,να ειναι η οριζουσα
Vandermonde διαφορη του 0.Ομως αυτο ισουται με $a_1a_2...a_n\prod_{i\not=j}\ (r^2_i-r^2_j)$ το οποιο οντως ειναι διαφορο του 0.
Απο εδω η λυση ειναι προφανης.

Ωραιότατη η γενίκευση, ακόμα καλύτερη η λύση.

#62

jimpav έγραψε: ↑
Κυρ Ιαν 21, 2018 1:37 am
1 θεμα απο β λυκειου?

Επειδή οι παρονομαστές είναι θετικοί για κάθε $\displaystyle x \in R$ , αφού έχουν αρνητικές διακρίνουσες και συντελεστή του x^2

θετικό, έχουμε ισοδύναμα:

$\displaystyle \frac{x}{{{x^2} + 2x + 3}} > \frac{{x + a}}{{{x^2} + x + 1}} \Leftrightarrow \left( {a + 1} \right){x^2} + 2\left( {a + 1} \right)x + 3a < 0$ .

Αν a = -1

η ανίσωση ισχύει για κάθε $\displaystyle x \in R$ .

Για $\displaystyle a \ne - 1$ η διακρίνουσά του είναι $\displaystyle D = 4\left( {a + 1} \right)\left( {1 - 2a} \right)$ .

Η ανίσωση αληθεύει για κάθε $\displaystyle x \in R$ αν και μόνο αν

$\displaystyle \left\{ \begin{array}{l} D < 0\\ \;\; \wedge \\ a + 1 < 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} \left( {a + 1} \right)\left( {1 - 2a} \right) < 0\\ \;\;\;\;\;\;\; \wedge \\ \;\;\;\;\;\;a < - 1 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} a < - 1\;\; \vee a > \frac{1}{2}\\ \;\;\;\;\;\;\; \wedge \\ \;\;\;a < - 1 \end{array} \right. \Leftrightarrow a < - 1$

Άρα πρέπει να είναι $\displaystyle a \le - 1$ .

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ · #63

Γιώργος Ρίζος έγραψε: ↑
Κυρ Ιαν 21, 2018 11:55 am

jimpav έγραψε: ↑
Κυρ Ιαν 21, 2018 1:37 am
1 θεμα απο β λυκειου?
Επειδή οι παρονομαστές είναι θετικοί για κάθε $\displaystyle x \in R$ , αφού έχουν αρνητικές διακρίνουσες και συντελεστή του θετικό, έχουμε ισοδύναμα:

$\displaystyle \frac{x}{{{x^2} + 2x + 3}} > \frac{{x + a}}{{{x^2} + x + 1}} \Leftrightarrow \left( {a + 1} \right){x^2} + 2\left( {a + 1} \right)x + 3a < 0$ .

Αν η ανίσωση ισχύει για κάθε $\displaystyle x \in R$ .

Για $\displaystyle a \ne - 1$ η διακρίνουσά του είναι $\displaystyle D = 4\left( {a + 1} \right)\left( {1 - 2a} \right)$ .

Η ανίσωση αληθεύει για κάθε $\displaystyle x \in R$ αν και μόνο αν

$\displaystyle \left\{ \begin{array}{l} D < 0\\ \;\; \wedge \\ a + 1 < 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} \left( {a + 1} \right)\left( {1 - 2a} \right) < 0\\ \;\;\;\;\;\;\; \wedge \\ \;\;\;\;\;\;a < - 1 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} a < - 1\;\; \vee a > \frac{1}{2}\\ \;\;\;\;\;\;\; \wedge \\ \;\;\;a < - 1 \end{array} \right. \Leftrightarrow a < - 1$

Άρα πρέπει να είναι $\displaystyle a \le - 1$ .

Από ένα σημείο και πέρα μπορούμε να κάνουμε το εξής:

Η $\left( {a + 1} \right){x^2} + 2\left( {a + 1} \right)x + 3a < 0$ .

για $a+1\neq 0$

γράφεται $(a+1)(x^{2}+2x+\frac{3a}{a+1})=(a+1)((x+1)^{2}+\frac{2a-1}{a+1})$

Η δεύτερη παρένθεση παίρνει πάντα και θετικές τιμές.

Αρα θα πρέπει a+1< 0

που για αυτά τα

ισχύει η ανίσωση.

kimjonarfib · #64

Γεια σας .
Εάν δεν διακρίναμε την περίπτωση α=-1 τότε πόσο προβλεπετε να χάσουμε;(Γνωρίζω ότι δεν ξέρετε άλλα ίσως να μπορείτε να υποθέσετε από την εμπειρία σας ως διορθωτές(ίσως)).

Ευχαριστώ

#65

achilleas έγραψε: ↑
Σάβ Ιαν 20, 2018 8:00 pm
Μια λύση του ΘΕΜΑΤΟΣ 4/Α ΛΥΚΕΙΟΥ δημοσιεύθηκε εδώ.

Ακολουθεί μια άλλη ιδέα βασισμένη στη "γνωστή" σχέση $1001=7\cdot 143.$

Παρατηρούμε ότι

$49000+1001=7\cdot 7000+7\cdot 143=7\cdot 7143,$

κι άρα

$7\cdot 7143=50001,$

ο οποίος λήγει σε 1 όταν διαιρεθεί με το

Έτσι, σκεφτόμαστε να βρούμε τα γινόμενα

$2007\cdot 7143=14336001$

και

$2007\cdot 2001=4016007$

Προσθέτοντας κατά μέλη βρίσκουμε $2007\cdot 9144=18352008$

(το $2007\cdot 1001=2009007$ και ο δεν λήγει σε . Γι' αυτό υπολογίζουμε το επόμενο $2007\cdot 2001$ )

και τα υπόλοιπα συνεχίζονται όπως στην παραπάνω πρώτη λύση.

Φιλικά,

Αχιλλέας

Μια ιδέα από μαθητή μας για την εύρεση του 9144.

Ψάχνουμε αριθμό $\overline{abcbd}$ τέτοιο ώστε $2007\cdot \overline{abcbd}=\dots 2008$

Λύνοντας την παρακάτω σχέση
$\begin{array}{ccccc} &2&0&0&7\\ \times &a&b&c&d\\ \hline .&2&0&0&8\\ \end{array}$

βρίσκουμε $\overline{abcd}=9144$ .

Για την αντιγραφή,

Αχιλλέας Συνεφακόπουλος

Μανώλης123 · #66

Έχω μια απορία. Το θέμα 3 Β γυμνασίου αν πούμε ότι το τρίγωνο είναι ισοσκελες για να υπολογίσουμε τις γωνιές είναι λάθος;;;;;;;;;;;;

#67

achilleas έγραψε: ↑
Σάβ Ιαν 20, 2018 12:50 pm
ΘΕΜΑ 2/Β ΛΥΚΕΙΟΥ

Είναι .

(Σχόλιο: Δε βλέπω πραγματική διαφορά από το Θέμα της Α. Στο ΘΕΜΑ 1της Α Λυκείου δείξαμε ότι $a_3, p\in \mathbb{Z}$ κι άρα το συμπέρασμα έπεται άμεσα.)

Διαφορετικά,

αρκεί να δειχθεί ότι ο είναι ακέραιος, όπως στο ΘΕΜΑ 1της Α Λυκείου.

Οι επίσημες ενδεικτικές λύσεις είναι διαθέσιμες εδώ.

Δεν καταλαβαίνω, όμως, γιατί στις λύσεις το Πρόβλημα 2 της Β Λυκείου εμφανίζεται ως Πρόβλημα 1.

Φιλικά,

Αχιλλέας

#68

Μανώλης123 έγραψε: ↑
Δευ Ιαν 22, 2018 6:08 pm
Έχω μια απορία. Το θέμα 3 Β γυμνασίου αν πούμε ότι το τρίγωνο είναι ισοσκελες για να υπολογίσουμε τις γωνιές είναι λάθος;;;;;;;;;;;;

Να υπολογίσουμε τη γωνία εννοείς, όχι τις γωνίες.

Ναι, λάθος είναι. Στη γεωμετρία δουλεύουμε με ένα τυχόν, γενικό τρίγωνο.

Το ισοσκελές είναι ειδική περίπτωση.

Τσιαλας Νικολαος · #69

achilleas έγραψε: ↑
Δευ Ιαν 22, 2018 7:59 pm

achilleas έγραψε: ↑
Σάβ Ιαν 20, 2018 12:50 pm
ΘΕΜΑ 2/Β ΛΥΚΕΙΟΥ

Είναι .

(Σχόλιο: Δε βλέπω πραγματική διαφορά από το Θέμα της Α. Στο ΘΕΜΑ 1της Α Λυκείου δείξαμε ότι $a_3, p\in \mathbb{Z}$ κι άρα το συμπέρασμα έπεται άμεσα.)

Διαφορετικά,

αρκεί να δειχθεί ότι ο είναι ακέραιος, όπως στο ΘΕΜΑ 1της Α Λυκείου.

Οι επίσημες ενδεικτικές λύσεις είναι διαθέσιμες εδώ.

Δεν καταλαβαίνω, όμως, γιατί στις λύσεις το Πρόβλημα 2 της Β Λυκείου εμφανίζεται ως Πρόβλημα 1.

Φιλικά,

Αχιλλέας

To αστείο της υπόθεσης είναι ότι και το 1ο της Α΄ και το δεύτερο της Β΄ λύνοντε σε 2 σειρές και δεν εμφανίστηκε η λύση αυτή!!!

Athena apo · #70

Στην γεωμετρία τη πρώτης Λυκείου αν πήρα τις πλευρές του ισοσκελους τραπεζιού την κάθε μια από 4 ρίζα δέκα και όχι από 2 ρίζα δέκα και έλυσα το πρόβλημα βρίσκοντας φυσικά λάθος νούμερα θα πάρω κάποιον βαθμό;

#71

Τσιαλας Νικολαος έγραψε: ↑
Δευ Ιαν 22, 2018 9:08 pm

achilleas έγραψε: ↑
Δευ Ιαν 22, 2018 7:59 pm

achilleas έγραψε: ↑
Σάβ Ιαν 20, 2018 12:50 pm
ΘΕΜΑ 2/Β ΛΥΚΕΙΟΥ

Είναι .

(Σχόλιο: Δε βλέπω πραγματική διαφορά από το Θέμα της Α. Στο ΘΕΜΑ 1της Α Λυκείου δείξαμε ότι $a_3, p\in \mathbb{Z}$ κι άρα το συμπέρασμα έπεται άμεσα.)

Διαφορετικά,

αρκεί να δειχθεί ότι ο είναι ακέραιος, όπως στο ΘΕΜΑ 1της Α Λυκείου.

Οι επίσημες ενδεικτικές λύσεις είναι διαθέσιμες εδώ.

Δεν καταλαβαίνω, όμως, γιατί στις λύσεις το Πρόβλημα 2 της Β Λυκείου εμφανίζεται ως Πρόβλημα 1.

Φιλικά,

Αχιλλέας
To αστείο της υπόθεσης είναι ότι και το 1ο της Α΄ και το δεύτερο της Β΄ λύνοντε σε 2 σειρές και δεν εμφανίστηκε η λύση αυτή!!!

Νίκο,

Ποια λύση έχεις στο νου σου;

Φιλικά,

Αχιλλέας

Michalis21 · #72

Καλησπέρα
Θεμα 1ο Γ Γυμνασίου,

Το έχω προχωρήσει μέχρι τη μέση και εκεί έκανα λάθος ένα πρόσημο και δεν έβγαλα 0 αποτέλεσμα.
Είναι λάθος όλο το πρόβλημα ή μπορεί να μου δώσουν κάποια μονάδα;
Ευχαριστώ πολύ.

Μήπως θα μπορούσε κάποιος να μου απαντήσει. Ευχαριστώ πολύ,.

Panagiotis11 · #73

Η λύση μου για το 2ο θέμα Β Λυκείου

Αρκεί να αποδείξουμε πως $x^5+y^5=(x^3+y^3)(x^2+y^2)-(xy)^2(x+y)\in \mathbb{Z}$
Δηλαδή αρκεί $x^3+y^3\wedge xy\in \mathbb{Z}$

$\bullet$ Ισχύει ότι $(x+y)^2\in \mathbb{Z}$ άρα $x^2+y^2+2xy\in \mathbb{Z}\Leftrightarrow 2xy\in \mathbb{Z}$ (1)

$\bullet$ Επίσης $(x^2+y^2)^2\in \mathbb{Z}\Leftrightarrow x^4+y^4+2(xy)^2\in \mathbb{Z}\Leftrightarrow 2(xy)^2\in \mathbb{Z}(2)$

Από $(2)-(1)\Rightarrow 2xy(xy-1)\in \mathbb{Z}\Leftrightarrow xy\in \mathbb{Z}$

Άρα και $(xy)^2\in \mathbb{Z}$ και $x^3+y^3=(x+y)(x^2-xy+y^2)\in \mathbb{Z}$ αφού $-xy=xy\cdot (-1)$

και η απόδειξη ολοκληρώθηκε.

#74

Panagiotis11 έγραψε: ↑
Τρί Ιαν 23, 2018 12:28 am
Η λύση μου για το 2ο θέμα Β Λυκείου

Αρκεί να αποδείξουμε πως $x^5+y^5=(x^3+y^3)(x^2+y^2)-(xy)^2(x+y)\in \mathbb{Z}$
Δηλαδή αρκεί $x^3+y^3\wedge xy\in \mathbb{Z}$

$\bullet$ Ισχύει ότι $(x+y)^2\in \mathbb{Z}$ άρα $x^2+y^2+2xy\in \mathbb{Z}\Leftrightarrow 2xy\in \mathbb{Z}$

$\bullet$ Επίσης $(x^2+y^2)^2\in \mathbb{Z}\Leftrightarrow x^4+y^4+2(xy)^2\in \mathbb{Z}\Leftrightarrow 2(xy)^2\in \mathbb{Z}(2)$

Από $(2)-(1)\Rightarrow 2xy(xy-1)\in \mathbb{Z}\Leftrightarrow xy\in \mathbb{Z}$

Άρα και $(xy)^2\in \mathbb{Z}$ και $x^3+y^3=(x+y)(x^2-xy+y^2)\in \mathbb{Z}$ αφού $-xy=xy\cdot (-1)$

και η απόδειξη ολοκληρώθηκε.

Δεν βλέπω γιατί $2xy(xy-1)\in \mathbb{Z}\implies xy\in \mathbb{Z}$ .

Νομίζω χρειάζεται απόδειξη.

(Προσθήκη: Για παράδειγμα: η εξίσωση 2a(a-1)=1

δεν έχει λύση ακέραιο.)

Φιλικά,

Αχιλλέας

eiriniz · #75

Καλησπέρα σας,

θα ήθελα να μου πείτε αν για το πρώτο θέμα της Β Λυκείου γράψαμε το εξής :

$\displaystyle x^2 + 2x + 3> x^2 + x + 1 \Rightarrow \frac{1}{x^2 + 2x +3} < \frac{1}{x^2+x+1}$ (1)
Aν $\alpha > 0$ τότε ισχύει $x < x + \alpha$ (2)

(1),(2) $\Rightarrow \frac{x}{x^2 + 2x +3} < \frac{x+\alpha}{x^2+x+1}$

Όμως εμείς θέλουμε το αντίθετο άρα $\alpha < 0$
θα παρούμε καμία μονάδα;
Και αν έχουμε λύσει παράλληλα το γ θεμα, στο δ να έχουμε αποδείξει το πρώτο ερώτημα και στο δεύτερο να έχουμε πει τι χρειάζεται να αποδείξουμε και στο 2ο θεμα να έχουμε γράψει κάτι (αν και να μην έχει απαντηθεί εν τέλει ).
Γενικότερα θα ήθελα να μου πει κάποιος αν έχω κάποιες πιθανότητες για πρόκριση στην επόμενη φάση.

Ευχαριστώ πολύ !

Τσιαλας Νικολαος · #76

achilleas έγραψε: ↑
Δευ Ιαν 22, 2018 10:34 pm

Τσιαλας Νικολαος έγραψε: ↑
Δευ Ιαν 22, 2018 9:08 pm

achilleas έγραψε: ↑
Δευ Ιαν 22, 2018 7:59 pm

achilleas έγραψε: ↑
Σάβ Ιαν 20, 2018 12:50 pm
ΘΕΜΑ 2/Β ΛΥΚΕΙΟΥ

Είναι .

(Σχόλιο: Δε βλέπω πραγματική διαφορά από το Θέμα της Α. Στο ΘΕΜΑ 1της Α Λυκείου δείξαμε ότι $a_3, p\in \mathbb{Z}$ κι άρα το συμπέρασμα έπεται άμεσα.)

Διαφορετικά,

αρκεί να δειχθεί ότι ο είναι ακέραιος, όπως στο ΘΕΜΑ 1της Α Λυκείου.

Οι επίσημες ενδεικτικές λύσεις είναι διαθέσιμες εδώ.

Δεν καταλαβαίνω, όμως, γιατί στις λύσεις το Πρόβλημα 2 της Β Λυκείου εμφανίζεται ως Πρόβλημα 1.

Φιλικά,

Αχιλλέας
To αστείο της υπόθεσης είναι ότι και το 1ο της Α΄ και το δεύτερο της Β΄ λύνοντε σε 2 σειρές και δεν εμφανίστηκε η λύση αυτή!!!
Νίκο,

Ποια λύση έχεις στο νου σου;

Φιλικά,

Αχιλλέας

Κύριε Αχιλλέα είμουν βιαστικός και απρόσεκτος και την πάτησα παρόμοια με τον Παναγιώτη από πάνω!!

mαre nostrum · #77

Α΄Λυκείου - Θέμα τρίτο

Πόσο χάνει κανείς που έχει ξεχάσει την περίπτωση το Ο να είναι εκτός του τραπεζίου;

Ευχαριστώ.

Eleftheria · #78

Ούτε εγώ πήρα αυτή την περίπτωση γιατί τότε δε θα ισαπειχαν οι κορυφές του τραπεζιου από το Ο. Έπρεπε δηλαδή να το πούμε αυτό; Είναι αυτονόητο.

#79

Eleftheria έγραψε: ↑
Τετ Ιαν 24, 2018 6:25 pm
Ούτε εγώ πήρα αυτή την περίπτωση γιατί τότε δε θα ισαπειχαν οι κορυφές του τραπεζιου από το Ο. Έπρεπε δηλαδή να το πούμε αυτό; Είναι αυτονόητο.

Πάρε έναν κύκλο και "πάνω" από το κέντρο φέρε δύο παράλληλες ευθείες. Τι σχήμα είναι αυτό που σχηματίζεται από τα τέσσερα σημεία τομής των παραλλήλων με τον κύκλο;

mαre nostrum έγραψε: ↑
Τετ Ιαν 24, 2018 5:10 pm
Α΄Λυκείου - Θέμα τρίτο

Πόσο χάνει κανείς που έχει ξεχάσει την περίπτωση το Ο να είναι εκτός του τραπεζίου;

Αν κάνεις μία λύση όπως η επίσημη που χρησιμοποιεί τη θέση του κέντρου, τότε αν δεν πάρεις τη μια περίπτωση χάνεις μία μονάδα.
Αν όμως κάνεις μία λύση όπως αυτή που εμφανίστηκε στο mathematica που δεν "αλλάζει" από τη θέση του κέντρου, τότε παίρνεις κανονικά όλες τις μονάδες.

Διονύσιος Αδαμόπουλος · #80

silouan έγραψε: ↑
Πέμ Ιαν 25, 2018 12:20 am

Eleftheria έγραψε: ↑
Τετ Ιαν 24, 2018 6:25 pm
Ούτε εγώ πήρα αυτή την περίπτωση γιατί τότε δε θα ισαπειχαν οι κορυφές του τραπεζιου από το Ο. Έπρεπε δηλαδή να το πούμε αυτό; Είναι αυτονόητο.
Πάρε έναν κύκλο και "πάνω" από το κέντρο φέρε δύο παράλληλες ευθείες. Τι σχήμα είναι αυτό που σχηματίζεται από τα τέσσερα σημεία τομής των παραλλήλων με τον κύκλο;

mαre nostrum έγραψε: ↑
Τετ Ιαν 24, 2018 5:10 pm
Α΄Λυκείου - Θέμα τρίτο

Πόσο χάνει κανείς που έχει ξεχάσει την περίπτωση το Ο να είναι εκτός του τραπεζίου;
Αν κάνεις μία λύση όπως η επίσημη που χρησιμοποιεί τη θέση του κέντρου, τότε αν δεν πάρεις τη μια περίπτωση χάνεις μία μονάδα.
Αν όμως κάνεις μία λύση όπως αυτή που εμφανίστηκε στο mathematica που δεν "αλλάζει" από τη θέση του κέντρου, τότε παίρνεις κανονικά όλες τις μονάδες.

Για να αποφευχθεί η χρήση του

μπορούμε να ακολουθήσουμε την εξής τακτική (επιγραμματικά):

Έχοντας ήδη φέρει το ύψος

και έχοντας υπολογίσει πως AB=10

και

προκύπτει ότι EC=12

.

Άρα έχουμε από πυθαγόρειο σε AEC

ότι $AC^2=EC^2+AE^2=144+36=180\Leftrightarrow AC=3\sqrt{20}$ .

Ταυτόχρονα στο ορθογώνιο τρίγωνο ADE

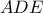έχουμε πως $\sin{\widehat{ADE}}=\dfrac{AE}{AD}=\dfrac{6}{2\sqrt{10}}=\dfrac{3}{\sqrt{10}}$ .

Επομένως $\sin{\widehat{ADC}}=\sin{\widehat{ADE}}=\dfrac{AE}{AD}=\dfrac{6}{2\sqrt{10}}=\dfrac{3}{\sqrt{10}}$

Εφαρμόζοντας τώρα νόμο ημιτόνων στο τρίγωνο ADC

προκύπτει ότι

$2R=\dfrac{AC}{\sin{\widehat{ADC}}}=\dfrac{3\sqrt{20}}{\dfrac{3}{\sqrt{10}}}=10\sqrt{2}\Leftrightarrow R=5\sqrt{2}$ .

ΕΥΚΛΕΙΔΗΣ 2017 - 2018

Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018

Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018

Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018

Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018

Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018

Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018

Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018

Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018

Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018

Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018

Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018

Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018

Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018

Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018

Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018

Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018

Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018

Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018

Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018

Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018

Μέλη σε σύνδεση