ΕΥΚΛΕΙΔΗΣ 2017 - 2018
Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5561
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
ΕΥΚΛΕΙΔΗΣ 2017 - 2018
Αυτά είναι τα θέματα του ΕΥΚΛΕΙΔΗ για το 2018 !
Γράψτε τις ωραίες και αναλυτικές λύσεις σας για το αρχείο του mathematica.
Καλά αποτελέσματα σε όλους τους συμμετέχοντες !
(ΑΝΑΡΤΗΣΗ : 12 πμ)
Γράψτε τις ωραίες και αναλυτικές λύσεις σας για το αρχείο του mathematica.
Καλά αποτελέσματα σε όλους τους συμμετέχοντες !
(ΑΝΑΡΤΗΣΗ : 12 πμ)
- Συνημμένα
-
- ΘΕΜΑΤΑ ΕΥΚΛΕΙΔΗ_2018_01_20_ΤΕΛΙΚΟ.pdf
- (428.35 KiB) Μεταφορτώθηκε 1588 φορές
τελευταία επεξεργασία από Μπάμπης Στεργίου σε Σάβ Ιαν 20, 2018 11:58 am, έχει επεξεργασθεί 3 φορές συνολικά.
Λέξεις Κλειδιά:
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018
Οι λύσεις θα συζητηθούν μετά τη λήξη του διαγωνισμού που θα είναι περίπου στις 12.
Αλέξανδρος
Αλέξανδρος
Αλέξανδρος Συγκελάκης
-
Τσιαλας Νικολαος
- Δημοσιεύσεις: 789
- Εγγραφή: Σάβ Ιαν 17, 2015 1:04 pm
Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018
Μπορεί κάποιος να ανεβάσει τα θέματα?? Έχουμε 12 παιδιά που συμμετέχουν και έχουμε λίγη αγωνία!! 

- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018
Νίκο και τα θέματα θα ανέβουν μετά τις 12 μετά από επικοινωνία με την επιτροπή διαγωνισμών της ΕΜΕ.Τσιαλας Νικολαος έγραψε: ↑Σάβ Ιαν 20, 2018 10:22 amΜπορεί κάποιος να ανεβάσει τα θέματα?? Έχουμε 12 παιδιά που συμμετέχουν και έχουμε λίγη αγωνία!!

Αλέξανδρος
Αλέξανδρος Συγκελάκης
-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5561
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018
ΘΕΜΑ 1/Α ΛΥΚΕΙΟΥ
Έστω
Είναι
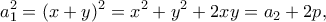
οπότε
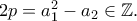
Ομοίως,
Αφού είναι άρτιος ακέραιος, οι ακέραιοι αριθμοί
είναι άρτιος ακέραιος, οι ακέραιοι αριθμοί  θα είναι και οι δύο άρτιοι ή και οι δύο περιττοί.
θα είναι και οι δύο άρτιοι ή και οι δύο περιττοί.
Αν είναι και οι δύο άρτιοι και
και  , (με
, (με  ), τότε
), τότε

κι έτσι

Αν είναι και οι δύο περιττοί και
και  , τότε
, τότε

κι άρα

Σε κάθε περίπτωση κι άρα
κι άρα 
Έστω

Είναι
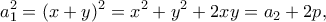
οπότε
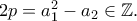
Ομοίως,

Αφού
 είναι άρτιος ακέραιος, οι ακέραιοι αριθμοί
είναι άρτιος ακέραιος, οι ακέραιοι αριθμοί  θα είναι και οι δύο άρτιοι ή και οι δύο περιττοί.
θα είναι και οι δύο άρτιοι ή και οι δύο περιττοί. Αν είναι και οι δύο άρτιοι
 και
και  , (με
, (με  ), τότε
), τότε
κι έτσι

Αν είναι και οι δύο περιττοί
 και
και  , τότε
, τότε
κι άρα

Σε κάθε περίπτωση
 κι άρα
κι άρα 
τελευταία επεξεργασία από achilleas σε Σάβ Ιαν 20, 2018 1:50 pm, έχει επεξεργασθεί 5 φορές συνολικά.
Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018
Α ΛΥΚΕΙΟΥ-ΘΕΜΑ 2
Είναι

Άρα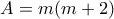 όπου
όπου 
(α) Παρατηρούμε ότι αν ο είναι άρτιος, τότε προφανώς ο
είναι άρτιος, τότε προφανώς ο  είναι κι αυτός άρτιος. Αν ο
είναι κι αυτός άρτιος. Αν ο  είναι περιττός, τότε ο
είναι περιττός, τότε ο  είναι άρτιος, κι άρα ο
είναι άρτιος, κι άρα ο  είναι άρτιος. Σε κάθε περίπτωση, λοιπόν, ο
είναι άρτιος. Σε κάθε περίπτωση, λοιπόν, ο  είναι άρτιος, κι το ίδιο είναι κι ο
είναι άρτιος, κι το ίδιο είναι κι ο 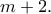
Συνεπώς, ο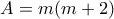 είναι γινόμενο δύο διαδοχικών άρτιων ακεραίων.
είναι γινόμενο δύο διαδοχικών άρτιων ακεραίων.
(β) Είναι

Η δεξιά ανισότηα είναι προφανής. Η αριστερή έπεται ισοδύναμα από την

που ισχύει αφού κι άρα
κι άρα 
Συνεπώς, ο βρίσκεται μεταξύ δύο διαδοχικών τετραγώνων ακεραίων, κι άρα δεν είναι τέλειο τετράγωνο.
βρίσκεται μεταξύ δύο διαδοχικών τετραγώνων ακεραίων, κι άρα δεν είναι τέλειο τετράγωνο.
Είναι

Άρα
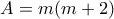 όπου
όπου 
(α) Παρατηρούμε ότι αν ο
 είναι άρτιος, τότε προφανώς ο
είναι άρτιος, τότε προφανώς ο  είναι κι αυτός άρτιος. Αν ο
είναι κι αυτός άρτιος. Αν ο  είναι περιττός, τότε ο
είναι περιττός, τότε ο  είναι άρτιος, κι άρα ο
είναι άρτιος, κι άρα ο  είναι άρτιος. Σε κάθε περίπτωση, λοιπόν, ο
είναι άρτιος. Σε κάθε περίπτωση, λοιπόν, ο  είναι άρτιος, κι το ίδιο είναι κι ο
είναι άρτιος, κι το ίδιο είναι κι ο 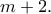
Συνεπώς, ο
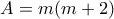 είναι γινόμενο δύο διαδοχικών άρτιων ακεραίων.
είναι γινόμενο δύο διαδοχικών άρτιων ακεραίων.(β) Είναι

Η δεξιά ανισότηα είναι προφανής. Η αριστερή έπεται ισοδύναμα από την

που ισχύει αφού
 κι άρα
κι άρα 
Συνεπώς, ο
 βρίσκεται μεταξύ δύο διαδοχικών τετραγώνων ακεραίων, κι άρα δεν είναι τέλειο τετράγωνο.
βρίσκεται μεταξύ δύο διαδοχικών τετραγώνων ακεραίων, κι άρα δεν είναι τέλειο τετράγωνο.Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018
Α ΛΥΚΕΙΟΥ-ΘΕΜΑ 3
Το άθροσμα των βάσεων του τραπεζίου είναι![\dfrac{2[AB\Gamma\Delta]}{h}=\dfrac{144}{6}=24. \dfrac{2[AB\Gamma\Delta]}{h}=\dfrac{144}{6}=24.](/forum/ext/geomar/texintegr/latexrender/pictures/2619f8aa0fec2e27052413640cf03619.png)
Το μήκος μιας μη παράλληλης πλευράς είναι Αν φέρουμε κάθετο τμήμα από το
Αν φέρουμε κάθετο τμήμα από το  στη μεγάλη βάση
στη μεγάλη βάση  , στο
, στο  , τότε από το Πυθαγόρειο θεώρημα θα έχουμε
, τότε από το Πυθαγόρειο θεώρημα θα έχουμε

Έτσι, η μικρή βάση τους τραπεζίου είναι και η μεγάλη είναι
και η μεγάλη είναι 
Από το Πυθαγόρειο στο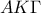 βρίσκουμε
βρίσκουμε 
Αν φέρουμε τη διάμετρο , τότε τα τρίγωνα
, τότε τα τρίγωνα 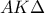 και
και  είναι όμοια, οπότε
είναι όμοια, οπότε  Η ζητούμενη ακτίνα είναι
Η ζητούμενη ακτίνα είναι
 μέτρα.
μέτρα.
Το άθροσμα των βάσεων του τραπεζίου είναι
![\dfrac{2[AB\Gamma\Delta]}{h}=\dfrac{144}{6}=24. \dfrac{2[AB\Gamma\Delta]}{h}=\dfrac{144}{6}=24.](/forum/ext/geomar/texintegr/latexrender/pictures/2619f8aa0fec2e27052413640cf03619.png)
Το μήκος μιας μη παράλληλης πλευράς είναι
 Αν φέρουμε κάθετο τμήμα από το
Αν φέρουμε κάθετο τμήμα από το  στη μεγάλη βάση
στη μεγάλη βάση  , στο
, στο  , τότε από το Πυθαγόρειο θεώρημα θα έχουμε
, τότε από το Πυθαγόρειο θεώρημα θα έχουμε
Έτσι, η μικρή βάση τους τραπεζίου είναι
 και η μεγάλη είναι
και η μεγάλη είναι 
Από το Πυθαγόρειο στο
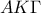 βρίσκουμε
βρίσκουμε 
Αν φέρουμε τη διάμετρο
 , τότε τα τρίγωνα
, τότε τα τρίγωνα 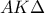 και
και  είναι όμοια, οπότε
είναι όμοια, οπότε  Η ζητούμενη ακτίνα είναι
Η ζητούμενη ακτίνα είναι μέτρα.
μέτρα.
τελευταία επεξεργασία από achilleas σε Σάβ Ιαν 20, 2018 1:44 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018
Α ΛΥΚΕΙΟΥ-ΘΕΜΑ 4
Θέλουμε όλους τους 6-ψηφιους για τους οποίους ο
για τους οποίους ο  αφήνει υπόλοιπο
αφήνει υπόλοιπο  όταν διαιρεθεί με το
όταν διαιρεθεί με το  Έτσι, ο
Έτσι, ο  θα είναι πολ/σιο του 10000.
θα είναι πολ/σιο του 10000.
Ο αλγόριθμος του Ευκλείδη για τη διαίρεση του με το 2007 δίνει
με το 2007 δίνει

ή

Έτσι, ο πρέπει να είναι εξαψήφιος της μορφής
πρέπει να είναι εξαψήφιος της μορφής  , δηλ.
, δηλ.  με
με

Λύνοντας την ανισότητα αυτή για ακέραιους βρίσκουμε ότι
βρίσκουμε ότι  , δηλ.
, δηλ.  .
.
Άρα υπάρχουν τέτοιοι αριθμοί.
τέτοιοι αριθμοί.
Θέλουμε όλους τους 6-ψηφιους
 για τους οποίους ο
για τους οποίους ο  αφήνει υπόλοιπο
αφήνει υπόλοιπο  όταν διαιρεθεί με το
όταν διαιρεθεί με το  Έτσι, ο
Έτσι, ο  θα είναι πολ/σιο του 10000.
θα είναι πολ/σιο του 10000.Ο αλγόριθμος του Ευκλείδη για τη διαίρεση του
 με το 2007 δίνει
με το 2007 δίνει
ή

Έτσι, ο
 πρέπει να είναι εξαψήφιος της μορφής
πρέπει να είναι εξαψήφιος της μορφής  , δηλ.
, δηλ.  με
με
Λύνοντας την ανισότητα αυτή για ακέραιους
 βρίσκουμε ότι
βρίσκουμε ότι  , δηλ.
, δηλ.  .
. Άρα υπάρχουν
 τέτοιοι αριθμοί.
τέτοιοι αριθμοί.
τελευταία επεξεργασία από achilleas σε Κυρ Ιαν 21, 2018 9:42 am, έχει επεξεργασθεί 2 φορές συνολικά.
Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018
ΘΕΜΑ 2/Β ΓΥΜΝΑΣΙΟΥ
Το γινόμενο όλων των δοθέντων αριθμών είναι .
.
Ο αριθμός 14 πρέπει να αφαιρεθεί οπωσδήποτε, διότι το 7 εμφανίζεται μόνο στην ανάλυση του 14. Το νέο γινόμενο θα είναι . Έτσι, θα πρέπει να αφαιρέσουμε άλλο ένα στοιχείο στο οποίο το 2 εμφανίζεται σε περιττό εκθέτη.
. Έτσι, θα πρέπει να αφαιρέσουμε άλλο ένα στοιχείο στο οποίο το 2 εμφανίζεται σε περιττό εκθέτη.
Αφαιρώντας, τον αριθμό 2 παίρνουμε γινόμενο

δηλ. τέλειο τετράγωνο.
Συνεπώς, ο ελάχιστος αριθμός στοιχείων που μπορούμε να αφαιρέσουμε είναι 2.
Το γινόμενο όλων των δοθέντων αριθμών είναι
 .
. Ο αριθμός 14 πρέπει να αφαιρεθεί οπωσδήποτε, διότι το 7 εμφανίζεται μόνο στην ανάλυση του 14. Το νέο γινόμενο θα είναι
 . Έτσι, θα πρέπει να αφαιρέσουμε άλλο ένα στοιχείο στο οποίο το 2 εμφανίζεται σε περιττό εκθέτη.
. Έτσι, θα πρέπει να αφαιρέσουμε άλλο ένα στοιχείο στο οποίο το 2 εμφανίζεται σε περιττό εκθέτη. Αφαιρώντας, τον αριθμό 2 παίρνουμε γινόμενο

δηλ. τέλειο τετράγωνο.
Συνεπώς, ο ελάχιστος αριθμός στοιχείων που μπορούμε να αφαιρέσουμε είναι 2.
τελευταία επεξεργασία από achilleas σε Σάβ Ιαν 20, 2018 2:24 pm, έχει επεξεργασθεί 1 φορά συνολικά.
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13272
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018
ΘΕΜΑ 4/Β ΓΥΜΝ
Έστω ότι ο Γιάννης είχε κέρματα του 1 ευρώ και
κέρματα του 1 ευρώ και  κέρματα των 2 ευρώ. Την πρώτη μέρα ξόδεψε
κέρματα των 2 ευρώ. Την πρώτη μέρα ξόδεψε  2-ευρα, και του απόμειναν
2-ευρα, και του απόμειναν  ευρώ συνολικά, από τα οποία ξόδεψε
ευρώ συνολικά, από τα οποία ξόδεψε  τη δεύτερη μέρα.
τη δεύτερη μέρα.
Συνολικά, λοιπόν, ξόδεψε ευρώ.
ευρώ.
Έτσι, οπότε
οπότε  .
.
Αφού ο αρχικός αριθμός των κερμάτων είναι , παίρνουμε
, παίρνουμε 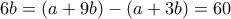 , οπότε
, οπότε 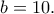
Ετσι, ο Γιάννης είχε 30 κέρματα των 2 ευρώ.
Έστω ότι ο Γιάννης είχε
 κέρματα του 1 ευρώ και
κέρματα του 1 ευρώ και  κέρματα των 2 ευρώ. Την πρώτη μέρα ξόδεψε
κέρματα των 2 ευρώ. Την πρώτη μέρα ξόδεψε  2-ευρα, και του απόμειναν
2-ευρα, και του απόμειναν  ευρώ συνολικά, από τα οποία ξόδεψε
ευρώ συνολικά, από τα οποία ξόδεψε  τη δεύτερη μέρα.
τη δεύτερη μέρα.Συνολικά, λοιπόν, ξόδεψε
 ευρώ.
ευρώ.Έτσι,
 οπότε
οπότε  .
. Αφού ο αρχικός αριθμός των κερμάτων είναι
 , παίρνουμε
, παίρνουμε 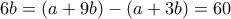 , οπότε
, οπότε 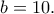
Ετσι, ο Γιάννης είχε 30 κέρματα των 2 ευρώ.
τελευταία επεξεργασία από achilleas σε Σάβ Ιαν 20, 2018 2:41 pm, έχει επεξεργασθεί 1 φορά συνολικά.
- matha
- Γενικός Συντονιστής
- Δημοσιεύσεις: 6423
- Εγγραφή: Παρ Μάιος 21, 2010 7:40 pm
- Τοποθεσία: Θεσσαλονίκη
Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018
ΘΕΜΑ 1ο Γ' Λυκείου
Επειδή η εξίσωση γράφεται
η εξίσωση γράφεται
 οπότε:
οπότε:
 Αν
Αν  η εξίσωση είναι αδύνατη
η εξίσωση είναι αδύνατη
 Αν
Αν  η εξίσωση έχει τη διπλή λύση
η εξίσωση έχει τη διπλή λύση 
 Αν
Αν  η εξίσωση έχει τις δύο λύσεις
η εξίσωση έχει τις δύο λύσεις 
Επειδή
 η εξίσωση γράφεται
η εξίσωση γράφεται οπότε:
οπότε: Αν
Αν  η εξίσωση είναι αδύνατη
η εξίσωση είναι αδύνατη Αν
Αν  η εξίσωση έχει τη διπλή λύση
η εξίσωση έχει τη διπλή λύση 
 Αν
Αν  η εξίσωση έχει τις δύο λύσεις
η εξίσωση έχει τις δύο λύσεις 
Μάγκος Θάνος
Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018
B Λυκείου 3o Η μέγιστη περιφέρεια ενός κύκλου στο εσωτερικό του ορθογωνίου λαμβάνεται όταν αυτό εφάπτεται σε  τουλάχιστον πλευρές και έχει μήκος το πολύ
τουλάχιστον πλευρές και έχει μήκος το πολύ  . Συνεπώς, πρέπει
. Συνεπώς, πρέπει  , από όπου έπεται το ζητούμενο.
, από όπου έπεται το ζητούμενο.
 τουλάχιστον πλευρές και έχει μήκος το πολύ
τουλάχιστον πλευρές και έχει μήκος το πολύ  . Συνεπώς, πρέπει
. Συνεπώς, πρέπει  , από όπου έπεται το ζητούμενο.
, από όπου έπεται το ζητούμενο.Bye :')
- matha
- Γενικός Συντονιστής
- Δημοσιεύσεις: 6423
- Εγγραφή: Παρ Μάιος 21, 2010 7:40 pm
- Τοποθεσία: Θεσσαλονίκη
Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018
ΘΕΜΑ 2ο Γ' Λυκείου:
Είναι Αν υπήρχε τέτοιο
Αν υπήρχε τέτοιο  θα είχαμε
θα είχαμε  άρα
άρα

άρα

Από τις πρώτες δύο προκύπτει άτοπο.
άτοπο.
Είναι
 Αν υπήρχε τέτοιο
Αν υπήρχε τέτοιο  θα είχαμε
θα είχαμε  άρα
άρα
άρα

Από τις πρώτες δύο προκύπτει
 άτοπο.
άτοπο.Μάγκος Θάνος
Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018
ΘΕΜΑ 2/Β ΛΥΚΕΙΟΥ
Είναι .
.
(Σχόλιο: Δε βλέπω πραγματική διαφορά από το Θέμα της Α. Στο ΘΕΜΑ 1της Α Λυκείου δείξαμε ότι κι άρα το συμπέρασμα έπεται άμεσα.)
κι άρα το συμπέρασμα έπεται άμεσα.)
Διαφορετικά,

αρκεί να δειχθεί ότι ο είναι ακέραιος, όπως στο ΘΕΜΑ 1της Α Λυκείου.
είναι ακέραιος, όπως στο ΘΕΜΑ 1της Α Λυκείου.
Είναι
 .
.(Σχόλιο: Δε βλέπω πραγματική διαφορά από το Θέμα της Α. Στο ΘΕΜΑ 1της Α Λυκείου δείξαμε ότι
 κι άρα το συμπέρασμα έπεται άμεσα.)
κι άρα το συμπέρασμα έπεται άμεσα.)Διαφορετικά,

αρκεί να δειχθεί ότι ο
 είναι ακέραιος, όπως στο ΘΕΜΑ 1της Α Λυκείου.
είναι ακέραιος, όπως στο ΘΕΜΑ 1της Α Λυκείου.
τελευταία επεξεργασία από achilleas σε Σάβ Ιαν 20, 2018 3:00 pm, έχει επεξεργασθεί 4 φορές συνολικά.
- polysot
- Επιμελητής
- Δημοσιεύσεις: 2583
- Εγγραφή: Δευ Οκτ 19, 2009 11:43 pm
- Τοποθεσία: Όπου βρω ενδιαφέρουσες προσωπικότητες...
- Επικοινωνία:
Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018
Τα θέματα δεν τα βλέπω!
Σωτήρης Δ. Χασάπης
Ζήσε τα μαθηματικά σου!
-----------------------------
"There is a scientific taste just as there is a literary or artistic one", Renan
"The journey of a thousand miles begins with one step.", Lao Tzu
Ζήσε τα μαθηματικά σου!
-----------------------------
"There is a scientific taste just as there is a literary or artistic one", Renan
"The journey of a thousand miles begins with one step.", Lao Tzu
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13272
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: ΕΥΚΛΕΙΔΗΣ 2017 - 2018
Θέμα 4 Β Λυκείου
Το  είναι ισοσκελές, άρα το
είναι ισοσκελές, άρα το  βρίσκεται στη μεσοκάθετο του
βρίσκεται στη μεσοκάθετο του  που είναι κάθετη και στην
που είναι κάθετη και στην  οπότε εφάπτεται του κύκλου
οπότε εφάπτεται του κύκλου 
 που αποδεικνύει και το δεύτερο ζητούμενο(σχέση εγγεγραμμένης και γωνίας χορδής εφαπτομένης).
που αποδεικνύει και το δεύτερο ζητούμενο(σχέση εγγεγραμμένης και γωνίας χορδής εφαπτομένης).
 είναι ισοσκελές, άρα το
είναι ισοσκελές, άρα το  βρίσκεται στη μεσοκάθετο του
βρίσκεται στη μεσοκάθετο του  που είναι κάθετη και στην
που είναι κάθετη και στην  οπότε εφάπτεται του κύκλου
οπότε εφάπτεται του κύκλου 
 που αποδεικνύει και το δεύτερο ζητούμενο(σχέση εγγεγραμμένης και γωνίας χορδής εφαπτομένης).
που αποδεικνύει και το δεύτερο ζητούμενο(σχέση εγγεγραμμένης και γωνίας χορδής εφαπτομένης).Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Bing [Bot] και 4 επισκέπτες

