(α) Να απλοποιήσετε το κλάσμα

(β) Να αποδείξετε ότι ο
 διαιρείται με το
διαιρείται με το  για κάθε φυσικό αριθμό
για κάθε φυσικό αριθμό  .
.Πρόβλημα 2
Αν ισχύει
 να αποδείξετε ότι:
να αποδείξετε ότι:(α)

(β)

Πρόβλημα 3
(α) Να αποδείξετε ότι οι πραγματικές ρίζες της εξίσωσης
 είναι
είναι  .
.(β) Δίνεται ότι
 και
και ![y = \sqrt[3]{2x-1}\, y \in \mathbb{R} \qquad (2) y = \sqrt[3]{2x-1}\, y \in \mathbb{R} \qquad (2)](/forum/ext/geomar/texintegr/latexrender/pictures/5f6625cc3d717298dd11f0ec6ba5915d.png)
(i) Να αποδείξετε ότι ισχύει:

(ii) Να βρείτε όλες τις τιμές
 που ικανοποιούν την εξίσωση (1)
που ικανοποιούν την εξίσωση (1)Πρόβλημα 4
Δίνεται τετράγωνο
 . Έστω σημείο
. Έστω σημείο  πάνω στην πλευρά
πάνω στην πλευρά  του τετραγώνου. Η διχοτόμος της γωνίας
του τετραγώνου. Η διχοτόμος της γωνίας  τέμνει την πλευρά
τέμνει την πλευρά  στο σημείο
στο σημείο  . Από το σημείο
. Από το σημείο  φέρουμε κάθετη ευθεία προς την
φέρουμε κάθετη ευθεία προς την  η οποία τέμνει την ευθεία
η οποία τέμνει την ευθεία  στο σημείο
στο σημείο  . Να αποδείξετε ότι
. Να αποδείξετε ότι  .
.


 είναι προφανώς άρτιος, ενώ ο
είναι προφανώς άρτιος, ενώ ο  ως γινόμενο τριών
ως γινόμενο τριών  . Άρα ο
. Άρα ο 
 άρα
άρα 
 είναι ίσα και
είναι ίσα και 

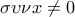


 είναι οξεία τότε
είναι οξεία τότε 