Πρόβλημα 1. Υπάρχει άραγε φυσικός αριθμός
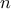 τέτοιος, ώστε οι αριθμοί
τέτοιος, ώστε οι αριθμοί 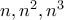 να ξεκινούν με το ίδιο ψηφίο, διάφορο του ένα; (Μπακάεβ)
να ξεκινούν με το ίδιο ψηφίο, διάφορο του ένα; (Μπακάεβ)Πρόβλημα 2. Σε κύκλο με κάποια σειρά είναι τοποθετημένοι όλοι οι φυσικοί αριθμοί από το 1 έως το 1000 με τέτοιο τρόπο, ώστε οποιοσδήποτε από τους αριθμούς να είναι διαιρέτης του αθροίσματος των δυο γειτονικών του. Είναι γνωστό, ότι δίπλα στον αριθμό
 βρίσκονται δυο περιττοί αριθμοί. Τι μπορεί να είναι ο αριθμός
βρίσκονται δυο περιττοί αριθμοί. Τι μπορεί να είναι ο αριθμός  , περιττός ή άρτιος; (Φρένκιν)
, περιττός ή άρτιος; (Φρένκιν)Πρόβλημα 3. Κάθε μέρα ο Φρένκεν Μποκ φτιάχνει μια τετραγωνική τούρτα διαστάσεων
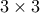 . O Κάρλσον(*) αμέσως κόβει από αυτήν για τον εαυτό του τέσσερα τετραγωνικά κομμάτια διαστάσεων
. O Κάρλσον(*) αμέσως κόβει από αυτήν για τον εαυτό του τέσσερα τετραγωνικά κομμάτια διαστάσεων 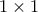 με πλευρές, παράλληλες προς τις πλευρές της τούρτας (όχι απαραίτητα κατά μήκος του
με πλευρές, παράλληλες προς τις πλευρές της τούρτας (όχι απαραίτητα κατά μήκος του 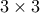 πλέγματος). Μετά από αυτό ο Μικρούλης κόβει από τα εναπομείναντα κομμάτια της τούρτας τετραγωνικό κομμάτι με πλευρές, επίσης παράλληλες με τις πλευρές της τούρτας. Ποιο είναι το μεγαλύτερο κομμάτι τούρτας που μπορεί να υπολογίζει ο Μικρούλης ανεξάρτητα του τι θα κάνει ο Κάρλσον; (Μπακάεβ)
πλέγματος). Μετά από αυτό ο Μικρούλης κόβει από τα εναπομείναντα κομμάτια της τούρτας τετραγωνικό κομμάτι με πλευρές, επίσης παράλληλες με τις πλευρές της τούρτας. Ποιο είναι το μεγαλύτερο κομμάτι τούρτας που μπορεί να υπολογίζει ο Μικρούλης ανεξάρτητα του τι θα κάνει ο Κάρλσον; (Μπακάεβ)Πρόβλημα 4. Έστω
 και
και 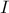 τα κέντρα του περιγεγραμμένου και εγγεγραμμένου κύκλου του μη ισοσκελούς τριγώνου
τα κέντρα του περιγεγραμμένου και εγγεγραμμένου κύκλου του μη ισοσκελούς τριγώνου  . Δυο ίσοι κύκλοι εφάπτονται των πλευρών
. Δυο ίσοι κύκλοι εφάπτονται των πλευρών 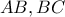 και
και  αντίστοιχα, καθώς και μεταξύ τους στο σημείο
αντίστοιχα, καθώς και μεταξύ τους στο σημείο 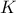 . Προέκυψε, ότι το σημείο
. Προέκυψε, ότι το σημείο 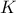 είναι σημείο της ευθείας
είναι σημείο της ευθείας  . Να βρείτε την γωνία
. Να βρείτε την γωνία 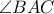 . (Ευδοκίμοβ)
. (Ευδοκίμοβ)Πρόβλημα 5. Ο αυτοκράτορας κάλεσε σε μια γιορτή 2015 αυλικούς, μερικοί από τους οποίους είναι καλοί και οι υπόλοιποι μοχθηροί. Οι καλοί αυλικοί πάντα λένε την αλήθεια, οι μοχθηροί όμως, ότι τους βολεύει. Εξάλλου οι αυλικοί γνωρίζουν ποιοι είναι καλοί και ποιοι μοχθηροί αλλά ο αυτοκράτορας όχι.
Στην γιορτή ο αυτοκράτορας θέτει σε κάθε αυλικό (με όποια σειρά θέλει) μια ερώτηση, στην οποία μπορούν να απαντήσουν με ένα «ναι» ή «όχι». Ρωτώντας όλους του αυλικούς ο αυτοκράτορας διώχνει έναν. Ο εκδιωχθείς αυλικός εξέρχεται από την μαγική πύλη, και ο αυτοκράτορας αναγνωρίζει αν είναι καλός ή μοχθηρός. Έπειτα από την αρχή ο αυτοκράτορας θέτει σε καθένα από τους εναπομείναντες αυλικούς μια ερώτηση, πάλι διώχνει έναν, και ούτω καθεξής, μέχρι να αποφασίσει να σταματήσει (μπορεί να το κάνει μετά από κάθε ερώτηση).
Να αποδείξετε, ότι ο αυτοκράτορας μπορεί να διώξει όλους τους μοχθηρούς αυλικούς, έχοντας την απώλεια το πολύ ενός καλού αυλικού. (Μιτροφάνοβ)
Πρόβλημα 6. Υπάρχουν άραγε δυο πολυώνυμα με ακέραιους συντελεστές τέτοια, ώστε το καθένα να τους να έχει συντελεστή κατά απόλυτη τιμή μεγαλύτερο του 2015, αλλά όλοι οι συντελεστές του γινομένου τους να μην υπερβαίνουν κατά απόλυτη τιμή το 1; (Κάνελ - Μπέλοβ)
(*) Φιγούρες δημοφιλούς κινουμένου σχεδίου σοβιετικής εποχής. Μεταφορά από σειρά παιδικών βιβλίων της σουηδή συγγραφέας Astrid Lindgren.

 είναι περιττός. Τότε έχουμε τρεις παραπάνω περιττούς και δεν μπορεί να επέλθει ισσοροπία αφού μετά από κάθε άρτιο (που τον ακολουθει περιττός αναγκαστικά) θέλουμε πάλι περιττό οπότε στην καλύτερη θα εχουμε εναν λιγότερο αρτιο από τους περιττούς ( τελειώνουμε με αρτιο).
είναι περιττός. Τότε έχουμε τρεις παραπάνω περιττούς και δεν μπορεί να επέλθει ισσοροπία αφού μετά από κάθε άρτιο (που τον ακολουθει περιττός αναγκαστικά) θέλουμε πάλι περιττό οπότε στην καλύτερη θα εχουμε εναν λιγότερο αρτιο από τους περιττούς ( τελειώνουμε με αρτιο). . Ρωτάω κάθε άλλο αυλικό αν ο
. Ρωτάω κάθε άλλο αυλικό αν ο  . Δεν κάνω άλλες ερωτήσεις και διώχνω των
. Δεν κάνω άλλες ερωτήσεις και διώχνω των  ο καλός αυλικός και
ο καλός αυλικός και  οι υπόλοιποι αυλικοί που έχουν μείνει. Για κάθε
οι υπόλοιποι αυλικοί που έχουν μείνει. Για κάθε  , ρωτάω των
, ρωτάω των  αν ο
αν ο  είναι καλός μέχρι να εισπράξω το πρώτο «ΟΧΙ».
είναι καλός μέχρι να εισπράξω το πρώτο «ΟΧΙ». . Τότε οι
. Τότε οι  είναι καλοί και ο
είναι καλοί και ο  . Είναι
. Είναι  και
και  ο οποίος επίσης ξεκινάει από
ο οποίος επίσης ξεκινάει από  . (Είναι
. (Είναι  .)
.)