Αλλές 3 ασκήσεις για διαγωνισμούς.

Datis-Kalali · #1

Όλες οι ασκήσεις είναι δική μου κατασκευής
1) Αν x,y,z

είναι διαφορετικοί θετικοί ακέραιοι να δείξετε ότι: $xyz(x^2+y^2+z^2-2) \ge 24(x+y+z-3)$
Πότε ισχυεί η ισότητα;
(Όμοια με το φετινό JBMO)*
2)Να δείξετε ότι δεν υπάρχουν τριψηφοί θετικοί ακέραιοι $\overline{abc}$ έτσι ώστε $\overline{abc}=ab+bc+ca$ με $abc \neq 0$
3)Έστω ABC

,

είναι ισοσκελές τρίγωνο με

και

τα μέσα τών

και

αντοίστοιχα. Το σημείο

είναι το ορθόκεντρο του τρίγωνου

με

και

τα μέσα τών

και

αντοίστοιχα.Αν O_1

και

είναι οι περίκεντροι τών τρίγωνων AHB

και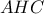

αντοίστοιχα, να δείξετε ότι ευθείες O_1C

,

και

συντρέχουν
*= Απο αυτό που κατάλαβω αυτή είναι την σωστή εκφωνήση του πρόβλημα. Η προυήγουμενή ήταν λάθος. Το διόρθωσα.

harrisp · #2

Datis-Kalali έγραψε:Όλες οι ασκήσεις είναι δική μου κατασκευής

2)Να δείξετε ότι δεν υπάρχουν τριψηφοί θετικοί ακέραιοι $\overline{abc}$ έτσι ώστε $\overline{abc}=ab+bc+ca$ με $abc \neq 0$

Καλησπέρα! Ελπίζω να είμαι σωστός...

Αν a>2

τότε θα πρέπει $\overline {3bc}\geq 311$ να είναι μικρότερο ή ίσο με το $ab+bc+ca\leq 3\cdot 81 = 243$ , άτοπο.

Αν τώρα a=1

τότε σύμφωνα με την δοσμένη:

100+9b=bc

που ειναι άτοπο αφού $LHS\geq 109<81\leq bc$ . Αρα $\boxed {a=2}$ .

Τότε με αντικατάσταση έχουμε: 200+8b=c(b+1)

και πάλι όμως είναι: $LHS\geq 208<90\leq c(b+1)$ .

Συνεπώς δεν υπάρχουν τριψήφιοι που να ικανοποιούν την αρχική σχέση.

Ορέστης Λιγνός · #3

Datis-Kalali έγραψε: 3)Έστω , είναι ισοσκελές τρίγωνο με και τα μέσα τών και αντοίστοιχα. Το σημείο είναι το ορθόκεντρο του τρίγωνου με και τα μέσα τών και αντοίστοιχα.Αν και είναι οι περίκεντροι τών τρίγωνων και αντοίστοιχα, να δείξετε ότι ευθείες , , , και συντρέχουν

Γεια σου Datis!

Είναι $MN, QL \parallel = \dfrac{BC}{2} \Rightarrow MN \parallel = QL$ , οπότε MNLQ

παραλληλόγραμμο.

Επίσης, $MQ \parallel AH \Rightarrow MQ \perp BC \Rightarrow MQ \perp MN$ , άρα MNLQ

ορθογώνιο παραλληλόγραμμο.

Έτσι, αν $S \equiv ML \cap QN$ , είναι $AM=AN, SM=SN \Rightarrow AS \perp MN \Rightarrow AS \perp BC$ , οπότε το

βρίσκεται πάνω στο ύψος

.

Τα τρίγωνα $\vartriangle O_1MB, \vartriangle O_2LC$ έχουν BM=NC

(αφού

,

(τα τρίγωνα $\vartriangle AHB , \vartriangle AHC$ είναι ίσα, οπότε έχουν ίσες ακτίνες) και είναι ορθογώνια, οπότε είναι ίσα.

Έτσι, O_1M=LC

και αφού $O_1M \perp AB, CL \perp AB \Rightarrow O_1M \parallel = LC$ , οπότε το O_1MCL

είναι παραλληλόγραμμο.

Έτσι, η O_1C

διέρχεται από το μέσο της

, το

.

Όμοια, η O_2B

διέρχεται από το

.

Η απόδειξη ολοκληρώθηκε.

: DATIS.png (29.63 KiB) Προβλήθηκε 1220 φορές

Datis-Kalali · #4

Επαναφορά.

#5

Datis-Kalali έγραψε: 1) Αν είναι διαφορετικοί θετικοί ακέραιοι να δείξετε ότι: $xyz(x^2+y^2+z^2-2) \ge 24(x+y+z-3)$
Πότε ισχυεί η ισότητα;
(Όμοια με το φετινό JBMO)

Κάπως πιο εύκολη από αυτήν της JBMO.

Θέλουμε να δείξουμε ότι

$\displaystyle{ x^3yz + xy^3z + xyz^3 + 72 \geqslant 2xyz + 24(x+y+z) }$

Μπορούμε να υποθέσουμε ότι $x \geqslant y \geqslant z$ , οπότε είναι και $x \geqslant 3, y \geqslant 2$ και $z \geqslant 1$ . Αυτές δίνουν

$\displaystyle{ x^3yz + xy^3z + xyz^3 \geqslant 9xyz + 4xyz + xyz}$

Αρκεί λοιπόν να δείξουμε ότι

$\displaystyle{ 14xyz + 72 \geqslant 2xyz + 24(x+y+z)}$

ή ισοδύναμα

$\displaystyle{ x(yz - 2) \geqslant 2y + 2z - 6}$

Αν z > 1

, τότε $yz \geqslant 3 \cdot 2 = 6$ . Οπότε

$\displaystyle{ x(yz - 2) \geqslant 4x > 2y + 2z > 2y + 2z - 6}$

και ισχύει αυστηρή ανισότητα.

Αν z=1

, τότε

$\displaystyle{ x(yz-2) - (2y+2z-6) = x(y-2) - (2y-4) = (x-2)(y-2) \geqslant 0}$

με ισότητα αν και μόνο αν y = 2

.

Οπότε η ανισότητα αποδείχθηκε. Για την ισότητα, στην περίπτωση $x \geqslant y \geqslant z$ , από αυτά που δείξαμε μέχρι τώρα πρέπει z=1

και

. Τότε θέλουμε
$\displaystyle{ 2x(x^2+3) = 24x}$
Άρα x^2+3=12

που δίνει

.

Άρα η ανισότητα ισχύει και έχουμε ισότητα αν και μόνο τα x,y,z

ισούνται με 1,2,3

με κάποια σειρά.

Ορέστης Λιγνός · #6

Datis-Kalali έγραψε:Όλες οι ασκήσεις είναι δική μου κατασκευής
1) Αν είναι διαφορετικοί θετικοί ακέραιοι να δείξετε ότι: $xyz(x^2+y^2+z^2-2) \ge 24(x+y+z-3)$
Πότε ισχυεί η ισότητα;
(Όμοια με το φετινό JBMO)*

Δίνω μία άλλη λύση.

Έστω z>y>x

, οπότε $z \geqslant 3, y \geqslant 2, x \geqslant 1$ .

Έτσι, $xyz \geqslant 6$ , οπότε $xyz(x^2+y^2+z^2-2) \geqslant 6(x^2+y^2+z^2-2)$

Αρκεί λοιπόν $6(x^2+y^2+z^2-2) \geqslant 24(x+y+z-3) \Rightarrow \ldots \Rightarrow (x-2)^2+(y-2)^2+(z-2)^2 \geqslant 2$ .

Αν $x-2,y-2,z-2 \neq 0$ , είναι $(x-2)^2 \geqslant 1 ,(y-2)^2 \geqslant 1,(z-2)^2 \geqslant 1$ , οπότε το ζητούμενο ισχύει.

Έστω τώρα ότι κάποιο από τα

είναι

.

Αν $x-2=0 \Rightarrow x=2 \Rightarrow y \geqslant 3, z \geqslant 4$ .

Οπότε, θέλουμε $(y-2)^2+(z-2)^2 \geqslant 2$ , που ισχύει διότι $(y-2)^2+(z-2)^2 \geqslant 1+4=5 >2$ .

Αν $y-2=0 \Rightarrow y=2,x=1$ θέλουμε $(z-2)^2 \geqslant 1$ , που είναι προφανές, διότι $z \geqslant 3$ .

Αν τέλος $z-2=0 \Rightarrow z=2 \Rightarrow 2>y>x>0$ , που είναι άτοπο.

Η ισότητα όταν x=1,y=2,z=3

και όλες οι μεταθέσεις.

Αλλές 3 ασκήσεις για διαγωνισμούς.

Αλλές 3 ασκήσεις για διαγωνισμούς.

Re: Αλλές 3 ασκήσεις για διαγωνισμούς.

Re: Αλλές 3 ασκήσεις για διαγωνισμούς.

Re: Αλλές 3 ασκήσεις για διαγωνισμούς.

Re: Αλλές 3 ασκήσεις για διαγωνισμούς.

Re: Αλλές 3 ασκήσεις για διαγωνισμούς.

Μέλη σε σύνδεση