Μαθηματική Ολυμπιάδα Α.Πετρούπολης 2017 (ΦΙ τάξη 6)

[Al.Koutsouridis]

[b][i]Μαθηματική Ολυμπιάδα Αγίας Πετρούπολης 2017

Θέματα της πρωτης φάσης για την 6η τάξη. [/i][/b] (*)


[b]1.[/b] Ο Ανδρέας σημείωσε στο ημερολόγιο 6 συνεχόμενες μέρες του Απρίλη και κατέγραψε τις ημερομηνίες που αντιστοιχούσαν σε αυτές τις μέρες. Προέκυψαν 6 διαδοχικοί αριθμοί, σε αύξουσα σειρά. Η Μαρία πολλαπλασίασε τους πρώτους τέσσερεις από αυτούς τους αριθμούς, η Ελένη τους τελευταίους τέσσερεις και ο Ανδρέας όλους εκτός από τους ακριανούς. Το τελευταίο ψηφίο των γινομένων της Μαρίας και της Ελένης συμπίπτουν, αλλά του Ανδρέα προέκυψε διαφορετικό τελευταίο ψηφίο. Ποιο; Βρείτε όλες τις δυνατές απαντήσεις και αποδείξτε, ότι άλλες δεν υπάρχουν.


[b]2.[/b] Σε έναν κυκλικό αυτοκινητόδρομο βρίσκονται πέντε χωριά. Από κάθε χωριό σε κάποια δυο, από τα υπόλοιπα χωριά, μπορούμε να μεταβούμε με λεωφορείο σε 2 ώρες, και στα εναπομείναντα δυο με ποδήλατο σε 4 ώρες (χωρίς να κάνουμε στάσεις και διερχόμενοι κατά την διάρκεια της διαδρομής το πολύ από ένα χωριό). Η ταχύτητα του λεωφορείου είναι πάντα ίδια, του ποδηλάτου και αυτή είναι πάντα ίδια αλλά μικρότερη του λεωφορείου. Σε πόση ώρα μπορούμε να κάνουμε όλη την κυκλική διαδρομή με το λεωφορείο;


[b]3.[/b] Σε πίνακα με 4 γραμμές και 9 στήλες υπάρχουν 9 κόκκινα κελιά, 11 μπλε και 16 άσπρα. Αν μετακινήσουμε το ποντίκι κατά γραμμή ή στήλη, συμβαίνει το εξής: αν σε αυτή την γραμμή/στήλη τα κελιά κάποιου χρώματος είναι περισσότερα, από καθένα από τα άλλα δυο χρώματα, τότε όλη η γραμμή/στήλη χρωματίζεται με αυτό το χρώμα. Αν δεν υπάρχει τέτοιο χρώμα, τότε δεν συμβαίνει (αλλάζει) τίποτα. Προέκυψε, ότι αν μετακινήσουμε το ποντίκι αρχικά κατά όλες τις γραμμές και έπειτα κατά όλες τις στήλες τότε όλα τα κελιά γίνονται κόκκινα. Και αν αντί για αυτό αρχικά μετακινήσουμε το ποντίκι κατά όλες τις στήλες και έπειτα κατά όλες τις γραμμές, τότε όλα τα κελιά γίνονται μπλε. Φέρτε παράδειγμα ενός τέτοιου πίνακα.


[b]4.[/b] Σε μια γειτονιά βρίσκονται 5 πολυκατοικίες, στις οποίες κατοικούν 5, 15, 25, 35, 45 άτομα. Είναι γνωστό, ότι ο καθένας τους έχει τουλάχιστον δυο συνονόματους μεταξύ των κατοίκων της γειτονιάς. Να αποδείξετε, ότι κάποιος έχει συνονόματο στην πολυκατοικία του.





[size=85](*) Στην επόμενη φάση πέρασαν όσοι έλυσαν 3(-) προβλήματα.[/size]

[Γιάννης Μπόρμπας]

Μαθηματική Ολυμπιάδα Αγίας Πετρούπολης 2017
4. Σε μια γειτονιά βρίσκονται 5 πολυκατοικίες, στις οποίες κατοικούν 5, 15, 25, 35, 45 άτομα. Είναι γνωστό, ότι ο καθένας τους έχει τουλάχιστον δυο συνονόματους μεταξύ των κατοίκων της γειτονιάς. Να αποδείξετε, ότι κάποιος έχει συνονόματο στην πολυκατοικία του.

Σύνολο οι άνθρωποι είναι . Αφού κάθε ένας έχει τουλάχιστον συνονόματους, τότε το κάθε όνομα θα εμφανίζεται τουλάχιστον
φορές. Όμως 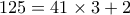, άρα υπάρχουν το πολύ διαφορετικά ονόματα, ενώ η πέμπτη πολυκατοικία έχει 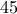άτομα, οπότε
τουλάχιστον από αυτούς θα είναι συνονόματοι.