Θέμα 4ο μεγάλων
Έχουμε

με μη αρνητικούς ακεραίους για συντελεστές και

, όπου

η θετική ρίζα του

.
1) Ισχυρίζομαι ότι

. Όντως παρατηρούμε ότι η τιμή αυτή ισούται με

. Το
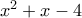
είναι ανάγωγο και άρα έχουμε τη (σημαντική) σχέση

στο
![\mathbb{Z}[X] \mathbb{Z}[X]](/forum/ext/geomar/texintegr/latexrender/pictures/dba144b0c7e9c5c01ae1a1d569bfea39.png)
. Άρα η ίδια σχέση διαιρετότητας ισχύει και στο
![\mathbb{Z}_2[X] \mathbb{Z}_2[X]](/forum/ext/geomar/texintegr/latexrender/pictures/49a594da2b62892519aa308686753203.png)
. Τότε

. Θέτω

και έχω

.
2) Πολύ ενδιαφέρον πρόβλημα! Η απάντηση είναι

. Για να το δείξω αυτό, γράφω

όπου το

ακέραιο πολυώνυμο και εξετάζω τους διαφόρους βαθμούς που μπορεί να πάρει το

a) Αν το

είναι σταθερό, έστω

τότε έχω

. Άρα

. Η ποσότητα που θέλουμε να ελαχιστοποιήσουμε είναι

. Συνεπώς
![min \begin{Bmatrix}P(1) \mid P \in \mathbb{Z}[X], a_i \geq 0, deg G =1 \end{Bmatrix} = -1008+2017 = 1009 min \begin{Bmatrix}P(1) \mid P \in \mathbb{Z}[X], a_i \geq 0, deg G =1 \end{Bmatrix} = -1008+2017 = 1009](/forum/ext/geomar/texintegr/latexrender/pictures/2977d7a0e0ce936af61895bcb49ed65d.png)
b) Αν το

είναι γραμμικό, έστω

τότε

. Θέλουμε όλοι οι συντελεστές να είναι μη αρνητικοί συνεπώς θέλουμε να ελαχιστοποιήσουμε την συνάρτηση

υπό τις συνθήκες

. Εύκολα λαμβάνουμε ότι το ελάχιστο είναι όταν

και έχει την τιμή

c) Για γενικό βαθμό

του

έστω

. Τότε έχουμε να ελαχιστοποιήσουμε την τιμή

υπό τις συνθήκες:

.
Άρα ας ξεκινήσουμε από το

. Μετά έχουμε

. Μετά έχουμε

. Συνεχίζουμε με τον ίδιο τρόπο μέχρι να μην μπορούμε να προχωρήσουμε άλλο. Τότε έχουμε ελάχιστο ίσο με

.
Το παραπάνω δεν είναι πολύ καλογραμμένο αλλά ελπίζω η ιδέα να είναι ξεκάθαρη. Τα συγχαρητήριά μου σε όποιον πρότεινε αυτό το πρόβλημα στον φετινό Αρχιμήδη.
Φιλικά,
Νίκος
 ζεύγη παικτών. Άρα, στους
ζεύγη παικτών. Άρα, στους  γύρους θα σχηματίζονται το πολύ
γύρους θα σχηματίζονται το πολύ  διαφορετικά ζεύγη παικτών.
διαφορετικά ζεύγη παικτών. θα πρέπει να ισχύει:
θα πρέπει να ισχύει:
 , αν οι παίκτες είναι Α, Β, Γ, Δ, Ε, Ζ και Η, τότε το παιχνίδι μπορεί να εξελιχθεί ως εξής:
, αν οι παίκτες είναι Α, Β, Γ, Δ, Ε, Ζ και Η, τότε το παιχνίδι μπορεί να εξελιχθεί ως εξής:

 και το εγγεγραμμένο
και το εγγεγραμμένο  προκύπτει ότι όλες οι κόκκινες γωνίες είναι ίσες μεταξύ τους και από το ισοσκελές
προκύπτει ότι όλες οι κόκκινες γωνίες είναι ίσες μεταξύ τους και από το ισοσκελές 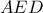 και οι γαλάζιες γωνίες είναι ίσες μεταξύ τους. Τέλος επειδή
και οι γαλάζιες γωνίες είναι ίσες μεταξύ τους. Τέλος επειδή  είναι το μέσο του
είναι το μέσο του  έχουμε
έχουμε  και το ζητούμενο έπεται.
και το ζητούμενο έπεται. .
. ένα από τον καθένα μπορούμε να φτιάξουμε τρίγωνα που φράζουν το
ένα από τον καθένα μπορούμε να φτιάξουμε τρίγωνα που φράζουν το  . Οι τρόποι επιλογής είναι
. Οι τρόποι επιλογής είναι  .
. σημεία τα οποία βρίσκονται σε διαφορετικούς τομείς από τα αρχικά και βρίσκονται στο ίδιο ημιεπίπεδο με το
σημεία τα οποία βρίσκονται σε διαφορετικούς τομείς από τα αρχικά και βρίσκονται στο ίδιο ημιεπίπεδο με το  . Αρα σύνολο υπάρχουν τουλάχιστον
. Αρα σύνολο υπάρχουν τουλάχιστον  τρίγωνα.
τρίγωνα. ότι
ότι  . Μετά εκτελώντας διαφορά τετραγώνων φτάνουμε εύκολα στην λύση. Περιμένω πως και πως να δω την λύση στο 4ο...
. Μετά εκτελώντας διαφορά τετραγώνων φτάνουμε εύκολα στην λύση. Περιμένω πως και πως να δω την λύση στο 4ο... .
.
 .
. τότε έχουμε ότι
τότε έχουμε ότι  και άρα
και άρα  οπότε έχουμε τη λύση
οπότε έχουμε τη λύση 
 είναι διαφορετικοί ανά δύο.
είναι διαφορετικοί ανά δύο.

 είναι θετικοί.
είναι θετικοί. (1)
(1) (2)
(2)
 και πως
και πως 
 .
. , άρα μοναδική λύση του συστήματος η
, άρα μοναδική λύση του συστήματος η 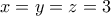 .
. με μη αρνητικούς ακεραίους για συντελεστές και
με μη αρνητικούς ακεραίους για συντελεστές και  , όπου
, όπου  η θετική ρίζα του
η θετική ρίζα του  .
.  . Όντως παρατηρούμε ότι η τιμή αυτή ισούται με
. Όντως παρατηρούμε ότι η τιμή αυτή ισούται με  . Το
. Το 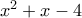 είναι ανάγωγο και άρα έχουμε τη (σημαντική) σχέση
είναι ανάγωγο και άρα έχουμε τη (σημαντική) σχέση  στο
στο ![\mathbb{Z}[X] \mathbb{Z}[X]](/forum/ext/geomar/texintegr/latexrender/pictures/dba144b0c7e9c5c01ae1a1d569bfea39.png) . Άρα η ίδια σχέση διαιρετότητας ισχύει και στο
. Άρα η ίδια σχέση διαιρετότητας ισχύει και στο ![\mathbb{Z}_2[X] \mathbb{Z}_2[X]](/forum/ext/geomar/texintegr/latexrender/pictures/49a594da2b62892519aa308686753203.png) . Τότε
. Τότε  . Θέτω
. Θέτω  και έχω
και έχω  .
. . Για να το δείξω αυτό, γράφω
. Για να το δείξω αυτό, γράφω  όπου το
όπου το  ακέραιο πολυώνυμο και εξετάζω τους διαφόρους βαθμούς που μπορεί να πάρει το
ακέραιο πολυώνυμο και εξετάζω τους διαφόρους βαθμούς που μπορεί να πάρει το 
 τότε έχω
τότε έχω  . Άρα
. Άρα  . Η ποσότητα που θέλουμε να ελαχιστοποιήσουμε είναι
. Η ποσότητα που θέλουμε να ελαχιστοποιήσουμε είναι  . Συνεπώς
. Συνεπώς ![min \begin{Bmatrix}P(1) \mid P \in \mathbb{Z}[X], a_i \geq 0, deg G =1 \end{Bmatrix} = -1008+2017 = 1009 min \begin{Bmatrix}P(1) \mid P \in \mathbb{Z}[X], a_i \geq 0, deg G =1 \end{Bmatrix} = -1008+2017 = 1009](/forum/ext/geomar/texintegr/latexrender/pictures/2977d7a0e0ce936af61895bcb49ed65d.png)
 τότε
τότε  . Θέλουμε όλοι οι συντελεστές να είναι μη αρνητικοί συνεπώς θέλουμε να ελαχιστοποιήσουμε την συνάρτηση
. Θέλουμε όλοι οι συντελεστές να είναι μη αρνητικοί συνεπώς θέλουμε να ελαχιστοποιήσουμε την συνάρτηση  υπό τις συνθήκες
υπό τις συνθήκες  . Εύκολα λαμβάνουμε ότι το ελάχιστο είναι όταν
. Εύκολα λαμβάνουμε ότι το ελάχιστο είναι όταν  και έχει την τιμή
και έχει την τιμή 
 του
του  . Τότε έχουμε να ελαχιστοποιήσουμε την τιμή
. Τότε έχουμε να ελαχιστοποιήσουμε την τιμή  υπό τις συνθήκες:
υπό τις συνθήκες:  .
. . Μετά έχουμε
. Μετά έχουμε  . Μετά έχουμε
. Μετά έχουμε  . Συνεχίζουμε με τον ίδιο τρόπο μέχρι να μην μπορούμε να προχωρήσουμε άλλο. Τότε έχουμε ελάχιστο ίσο με
. Συνεχίζουμε με τον ίδιο τρόπο μέχρι να μην μπορούμε να προχωρήσουμε άλλο. Τότε έχουμε ελάχιστο ίσο με  .
. με
με  το υπόλοιπο της Ευκλείδειας διαίρεσης
το υπόλοιπο της Ευκλείδειας διαίρεσης  και έστω
και έστω  το αντίστοιχο πηλίκο.
το αντίστοιχο πηλίκο. .
. είναι άρρητος, έχουμε
είναι άρρητος, έχουμε  , κι άρα
, κι άρα  .
. είναι περιττός.
είναι περιττός.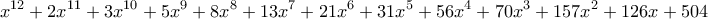
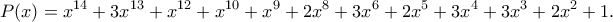
 αρνητικοί ακέραιοι και μόνο
αρνητικοί ακέραιοι και μόνο  θετικός. Οπότε βολεύει να κάνουμε την αντικατάσταση
θετικός. Οπότε βολεύει να κάνουμε την αντικατάσταση  για κάποιο ακέραιο
για κάποιο ακέραιο  . Η σχέση γίνεται:
. Η σχέση γίνεται: . Σε αυτό το σημείο ο μαθητής πρέπει να μυριστεί ότι:
. Σε αυτό το σημείο ο μαθητής πρέπει να μυριστεί ότι: . Άρα
. Άρα  η οποία ισοδύναμα γράφεται:
η οποία ισοδύναμα γράφεται: . Ο αριθμός
. Ο αριθμός είναι πρώτος και ο δεξιός παράγοντας είναι μεγαλύτερος του αριστερού διακρίνοντας τις περιπτώσεις:
είναι πρώτος και ο δεξιός παράγοντας είναι μεγαλύτερος του αριστερού διακρίνοντας τις περιπτώσεις: και
και όπου με αφαίρεση κατα μέλη έχουμε:
όπου με αφαίρεση κατα μέλη έχουμε: . Η διακρίνουσα του τριωνύμου πρέπει να είναι τέλειο τετράγωνο έστω
. Η διακρίνουσα του τριωνύμου πρέπει να είναι τέλειο τετράγωνο έστω . Άρα
. Άρα . Με έλεγχο παρατηρούμε ότι για
. Με έλεγχο παρατηρούμε ότι για προκύπτει η λύση:
προκύπτει η λύση: η οποία είναι δεκτή αφού
η οποία είναι δεκτή αφού .Η δεύτερη περίπτωση είναι:
.Η δεύτερη περίπτωση είναι: και
και . Πάλι με αφαίρεση κατά μέλη έχουμε:
. Πάλι με αφαίρεση κατά μέλη έχουμε: που είναι ίδια με την προηγούμενη άρα μοναδική λύση είναι ή
που είναι ίδια με την προηγούμενη άρα μοναδική λύση είναι ή  μπορεί να γραφεί ως:
μπορεί να γραφεί ως: . Αφού όμως
. Αφού όμως και
και πρέπει οι αριθμοί
πρέπει οι αριθμοί  να είναι ταυτόχρονα άρτιοι. Από εκεί μπορούμε να γλιτώσουμε περιπτώσεις χρησιμοποιώντας επίσης ότι
να είναι ταυτόχρονα άρτιοι. Από εκεί μπορούμε να γλιτώσουμε περιπτώσεις χρησιμοποιώντας επίσης ότι .
. που είναι άτοπο αφού
που είναι άτοπο αφού οπότε μοναδική λύση είναι η
οπότε μοναδική λύση είναι η .
. και
και  τότε έχουμε ότι
τότε έχουμε ότι ,
, είναι άρτιοι. Αν γράψουμε
είναι άρτιοι. Αν γράψουμε  και
και  τότε έχουμε ότι
τότε έχουμε ότι ,
, θα είναι:
θα είναι:
 οπότε
οπότε  και άρα
και άρα 
 και
και 