Σε συνέχεια του προηγούμενου θέματος, ακολουθούν τα προβλήματα του 2ου τεστ:
**********************************************
Practice TEST 2
ΔΙΑΡΚΕΙΑ: 4 ΩΡΕΣ
ΘΕΜΑ 1. Αν οι
 είναι ανά δύο διακεκριμμένοι πραγματικοί αριθμοί, να δειχθεί ότι η τιμή της παράστασης
είναι ανά δύο διακεκριμμένοι πραγματικοί αριθμοί, να δειχθεί ότι η τιμή της παράστασης
είναι πάντοτε μη μηδενική.
ΘΕΜΑ 2. Σε ισόπλευρο τρίγωνο
 παίρνουμε τα σημεία
παίρνουμε τα σημεία  στις πλευρές του
στις πλευρές του  αντίστοιχα, ώστε η
αντίστοιχα, ώστε η  να είναι παράλληλη στην
να είναι παράλληλη στην  . Έστω
. Έστω  το βαρύκεντρο του τριγώνου
το βαρύκεντρο του τριγώνου  και έστω
και έστω  το μέσο του τμήματος
το μέσο του τμήματος  . Να υπολογίσετε τις γωνίες του τριγώνου
. Να υπολογίσετε τις γωνίες του τριγώνου  .
.ΘΕΜΑ 3. Έστω
 μη αρνητικοί πραγματικοί αριθμοί, για τους οποίους ισχύει
μη αρνητικοί πραγματικοί αριθμοί, για τους οποίους ισχύει  . Να αποδείξετε ότι:
. Να αποδείξετε ότι:
Πότε ισχύει η ισότητα?
ΘΕΜΑ 4. Να βρεθούν όλοι οι θετικοί ακέραιοι
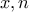 που ικανοποιούν την εξίσωση
που ικανοποιούν την εξίσωση 
**********************************************
Φιλικά,
Αχιλλέας

 ) , ισούται με
) , ισούται με  . Άρα η δοθείσα παράσταση ισούται με
. Άρα η δοθείσα παράσταση ισούται με 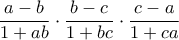
 και λοιπά, οπότε οι παραστάση ισούται με
και λοιπά, οπότε οι παραστάση ισούται με  και άρα με το γινόμενό τους αφού
και άρα με το γινόμενό τους αφού 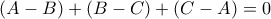 (γνωστή άσκηση). Οι λεπτομέρειες όμως φαίνονται λίγο δυσκολότερες από ότι την πρώτη λύση, οπότε ας μην μας απασχολήσει...
(γνωστή άσκηση). Οι λεπτομέρειες όμως φαίνονται λίγο δυσκολότερες από ότι την πρώτη λύση, οπότε ας μην μας απασχολήσει... . Συνεπώς πρέπει
. Συνεπώς πρέπει  .
.  με το
με το  είναι το
είναι το  , ενώ του
, ενώ του  είναι
είναι  .
.  . Όμως γνωρίζουμε πως
. Όμως γνωρίζουμε πως  (εδώ το
(εδώ το  είναι το ελάχιστο
είναι το ελάχιστο  που ισχύει κάτι τέτοιο), άρα
που ισχύει κάτι τέτοιο), άρα  ,
,  όπου θετικός ακέραιος.
όπου θετικός ακέραιος. .
. , ισχύει ότι:
, ισχύει ότι:  (1)
(1) , ισχύει ότι:
, ισχύει ότι:  (2)
(2)  και
και 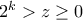 , τότε από τις σχέσεις (2) και (1) έχουμε ότι:
, τότε από τις σχέσεις (2) και (1) έχουμε ότι: , άτοπο. Άρα
, άτοπο. Άρα 
 , έχουμε τη μοναδική λύση
, έχουμε τη μοναδική λύση  .
.
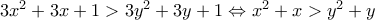 που ισχύει.
που ισχύει. , καθώς αν οι αριθμοί μεγαλώσουν περισσότερο, τότε οι διαφορές
, καθώς αν οι αριθμοί μεγαλώσουν περισσότερο, τότε οι διαφορές  ακόμα και διαδοχικών κύβων είναι μεγαλύτερες από
ακόμα και διαδοχικών κύβων είναι μεγαλύτερες από  .
.
 οπότε υπάρχουν
οπότε υπάρχουν  ώστε
ώστε 

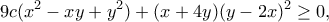 η οποία ισχύει.
η οποία ισχύει. δηλαδή
δηλαδή  ή
ή  και οι μεταθέσεις.
και οι μεταθέσεις. . Αν όμως
. Αν όμως 

 ,
, 
 .
. είναι επίσης ισόπλευρο και το βαρύκεντρό του θα είναι και ορθόκεντρο, οπότε η
είναι επίσης ισόπλευρο και το βαρύκεντρό του θα είναι και ορθόκεντρο, οπότε η  θα είναι κάθετη
θα είναι κάθετη  Το
Το  είναι λοιπόν εγγράψιμο. Αλλά και
είναι λοιπόν εγγράψιμο. Αλλά και  είναι εγγράψιμο,
είναι εγγράψιμο,  ) Επομένως τα
) Επομένως τα  είναι ομοκυκλικά,
είναι ομοκυκλικά,  και
και 