Θέματα της δεύτερης φάσης (τελικής) για την 8η τάξη. Διάρκεια εξέτασης 3 ώρες. (*)[/i][/b]
[b]1.[/b] Στο νησί Κακοτυχία οι άνδρες την Τετάρτη λένε πάντα την αλήθεια, ενώ την Πέμπτη πάντα ψεύδονται και οι γυναίκες το ανάποδο. Την Τετάρτη ο καθένας τους είπε «Ο αριθμός των ανδρών που γνωρίζω είναι κατά ένα μεγαλύτερος από τον αριθμό των γυναικών που γνωρίζω», και την Πέμπτη «Ο αριθμός των γυναικών που γνωρίζω είναι κατά ένα μεγαλύτερος από των αριθμό των ανδρών που γνωρίζω». Μπορεί το νησί να έχει ακριβώς 2015 κατοίκους;
[b]2.[/b] Δίνονται οι αριθμοί
 . Να αποδείξετε, ότι
. Να αποδείξετε, ότι 
[b]3.[/b] Σε ισοσκελές τρίγωνο
 (
( ) φέρουμε την διχοτόμο
) φέρουμε την διχοτόμο  . Στη βάση
. Στη βάση  δίνεται σημείο
δίνεται σημείο  , τέτοιο ώστε
, τέτοιο ώστε  . Η διχοτόμος της γωνίας
. Η διχοτόμος της γωνίας 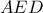 τέμνει την πλευρά
τέμνει την πλευρά  στο σημείο
στο σημείο  . Να αποδείξετε, ότι
. Να αποδείξετε, ότι  .
.[b]4.[/b] Τετράγωνο διαστάσεων
 κελιών, διαμερίζεται σε πλακίδια διαστάσεων
κελιών, διαμερίζεται σε πλακίδια διαστάσεων  . Να αποδείξετε, ότι μπορούμε να ορίσουμε μια τέτοια διαμέριση του τετραγώνου σε ορθογώνια διαστάσεων
. Να αποδείξετε, ότι μπορούμε να ορίσουμε μια τέτοια διαμέριση του τετραγώνου σε ορθογώνια διαστάσεων  , ώστε κάθε πλακίδιο
, ώστε κάθε πλακίδιο  να περιέχει τουλάχιστον ένα ολόκληρο ορθογώνιο.
να περιέχει τουλάχιστον ένα ολόκληρο ορθογώνιο. [b]Καταληκτική αίθουσα (**)[/b]
[b]5.[/b] Ο Βασίλης έγραψε σε μια γραμμή 100 διαδοχικούς αριθμούς. Στην δεύτερη γραμμή κάτω από κάθε αριθμό της πρώτης έγραψε ένα γνήσιο διαιρέτη του. Στην τρίτη γραμμή κάτω από κάθε αριθμό της δεύτερης γραμμής έγραψε έναν γνήσιο διαιρέτη του κ.ο.κ., μέχρι να φτάσει τις 1000 γραμμές. Είναι δυνατόν, κάθε γραμμή να αποτελείται από διαδοχικούς αριθμούς;
[b]6.[/b] Στο ράφι μιας αποθήκης είναι τοποθετημένες 13 βαλίτσες, αριθμημένες με κάποια σειρά με τους αριθμούς από το 1 έως το 13. Οι βαλίτσες έχουν διαφορετικά πλάτη και δεν είναι απαραίτητα κολλητά η μια στην άλλη και στα άκρα του ραφιού. Ο αποθηκάριος αφαιρεί την βαλίτσα
 και την τοποθετεί στην πιο αριστερά επιτρεπτή θέση, χωρίς να μετακινήσει τις άλλες βαλίτσες. Έπειτα αφαιρεί την βαλίτσα
και την τοποθετεί στην πιο αριστερά επιτρεπτή θέση, χωρίς να μετακινήσει τις άλλες βαλίτσες. Έπειτα αφαιρεί την βαλίτσα  και την τοποθετεί στην πιο αριστερά επιτρεπτή θέση, χωρίς να μετακινήσει τις άλλες βαλίτσες κ.ο.κ. Μετά και από την επανατοποθέτηση της βαλίτσας
και την τοποθετεί στην πιο αριστερά επιτρεπτή θέση, χωρίς να μετακινήσει τις άλλες βαλίτσες κ.ο.κ. Μετά και από την επανατοποθέτηση της βαλίτσας  ο αποθηκάριος εκ νέου συνεχίζει την διαδικασία με την βαλίτσα
ο αποθηκάριος εκ νέου συνεχίζει την διαδικασία με την βαλίτσα  κ.ο.κ. Να βρείτε τον μικρότερο φυσικό
κ.ο.κ. Να βρείτε τον μικρότερο φυσικό  τέτοιο, ώστε για οποιαδήποτε αρχική τοποθέτηση των βαλιτσών ύστερα από
τέτοιο, ώστε για οποιαδήποτε αρχική τοποθέτηση των βαλιτσών ύστερα από  επανατοποθετήσεις κάθε βαλίτσα ο αποθηκάριος με βεβαιότητα θα την τοποθετήσει σε εκείνη την θέση, από την οποία την πήρε. (αν η βαλίτσα τοποθετείτε στην θέση, από την οποία την πήρανε, τότε και αυτή η κίνηση προσμετράτε σαν επανατοποθέτηση).
επανατοποθετήσεις κάθε βαλίτσα ο αποθηκάριος με βεβαιότητα θα την τοποθετήσει σε εκείνη την θέση, από την οποία την πήρε. (αν η βαλίτσα τοποθετείτε στην θέση, από την οποία την πήρανε, τότε και αυτή η κίνηση προσμετράτε σαν επανατοποθέτηση).[b]7.[/b] Στο εσωτερικό τριγώνου
 δίνεται σημείο
δίνεται σημείο  , από το οποίο κάθε πλευρά φαίνεται υπό γωνία
, από το οποίο κάθε πλευρά φαίνεται υπό γωνία  . Να αποδείξετε, ότι
. Να αποδείξετε, ότι .
.[size=85][i](*) Η τελική φάση της ολυμπιάδας είναι προφορική.
(**) Όσοι έλυσαν τρία από τα τέσσερα αρχικά προβλήματα καλέστηκαν να λύσουν άλλα τρία σε διαφορετική αίθουσα. Ο επιπλέον χρόνος που δίνεται είναι μια ώρα.[/i]
Στατιστικά: Στον πρώτο πίνακα αναγράφεται ο αριθμός των λυτών ανά θέμα (πόσοι έλυσαν το πρώτο, δύτερο θέμα κτλ.). Στον δεύτερο πίνακα ο αριθμός των μαθητών ανά πλήθος θεμάτων που έλυσαν(πόσοι έλυσαν ένα, δυο κτλ θέματα).


Edit: 23/03/2017 έγινε διόρθωση των διαστάσεων του τετραγώνου στο πρόβλημα 4 και διόρθωση στην εκφώνηση του 5ου προβλήματος.[/size]

 , τότε ισχύει η ισότητα.
, τότε ισχύει η ισότητα.  και
και  έχουμε ότι
έχουμε ότι  .
. 



 έχουμε ότι:
έχουμε ότι:  (1)
(1) (2)
(2)
 παράλληλη προς την
παράλληλη προς την  . Επειδή θα είναι
. Επειδή θα είναι  , έχουμε πως το τρίγωνο
, έχουμε πως το τρίγωνο  είναι ισοσκελές, με
είναι ισοσκελές, με  .
. και
και  έχουμε ότι:
έχουμε ότι:
 .
. , άρα το
, άρα το 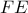 της γωνίας
της γωνίας  είναι και μεσοκάθετος του
είναι και μεσοκάθετος του  . Πράγματι λοιπόν
. Πράγματι λοιπόν 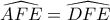 .
. ο αριθμός των γυναικών που γνωρίζει ένας άντρας τότε αφού λένε την αλήθεια οι άντρες τις Τετάρτες ο αρθμός των ανδρών που γνωρίζει θα είναι
ο αριθμός των γυναικών που γνωρίζει ένας άντρας τότε αφού λένε την αλήθεια οι άντρες τις Τετάρτες ο αρθμός των ανδρών που γνωρίζει θα είναι 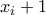 . Δηλαδή συνολικά ένας άνδρας γνωρίζει
. Δηλαδή συνολικά ένας άνδρας γνωρίζει  περιττό αριθμό ατόμων.
περιττό αριθμό ατόμων. γραμμές». Φαίνεται να υπονοεί ότι γίνεται αν δεν φτάσει τις
γραμμές». Φαίνεται να υπονοεί ότι γίνεται αν δεν φτάσει τις  διαδοχικούς αριθμούς τότε μπορώ αμέσως από πάνω από κάθε αριθμό να γράψω ένα γνήσιο πολλαπλάσιό του ώστε και η από πάνω γραμμή να αποτελείται από διαφορετικούς αριθμούς.
διαδοχικούς αριθμούς τότε μπορώ αμέσως από πάνω από κάθε αριθμό να γράψω ένα γνήσιο πολλαπλάσιό του ώστε και η από πάνω γραμμή να αποτελείται από διαφορετικούς αριθμούς. τότε από πάνω γράφω την γραμμή
τότε από πάνω γράφω την γραμμή  όπου
όπου  Ασφαλώς για
Ασφαλώς για  ο
ο  είναι ακέραιος μεγαλύτερος του
είναι ακέραιος μεγαλύτερος του  . Επιπλέον
. Επιπλέον
 κελιών, διαμερίζεται σε πλακίδια διαστάσεων
κελιών, διαμερίζεται σε πλακίδια διαστάσεων 


