Θέματα της 3ης φάσης για την 10η τάξη. Διάρκεια εξέτασης 4 ώρες/μέρα.
Πρώτη μέρα (30/01/17)
1. Σε γινόμενο πέντε μη μηδενικών φυσικών αριθμών κάθε παράγοντα των μειώνουμε κατά τρία. Μπορεί άραγε, με αυτή την διαδικασία, το γινόμενο να αυξηθεί ακριβώς κατά 15 φορές;
2. Κύκλος με κέντρο
 είναι εγγεγραμμένος σε τετράπλευρο
είναι εγγεγραμμένος σε τετράπλευρο  . Οι χορδές
. Οι χορδές  και
και  τέμνονται στο σημείο
τέμνονται στο σημείο  , και οι χορδές
, και οι χορδές  και
και  στο σημείο
στο σημείο  . Είναι γνωστό, ότι το σημείο
. Είναι γνωστό, ότι το σημείο  βρίσκεται επί του περιγεγραμμένου κύκλου
βρίσκεται επί του περιγεγραμμένου κύκλου  του τριγώνου
του τριγώνου  . Να αποδείξετε, ότι και το σημείο
. Να αποδείξετε, ότι και το σημείο  βρίσκεται επί του κύκλου
βρίσκεται επί του κύκλου  .
.3. Ο Παύλος διάλεξε 2017 (όχι απαραίτητα διαφορετικούς) μη μηδενικούς φυσικούς αριθμούς
 και παίζει μόνος του το ακόλουθο παιχνίδι. Στην αρχή έχει απεριόριστο απόθεμα από βότσαλα και 2017 μεγάλα άδεια κουτιά. Με μια κίνηση, ο Παύλος τοποθετεί σε οποιοδήποτε κουτί (της επιλογής του)
και παίζει μόνος του το ακόλουθο παιχνίδι. Στην αρχή έχει απεριόριστο απόθεμα από βότσαλα και 2017 μεγάλα άδεια κουτιά. Με μια κίνηση, ο Παύλος τοποθετεί σε οποιοδήποτε κουτί (της επιλογής του)  βότσαλα, σε οποιοδήποτε από τα εναπομείναντα κουτιά (της επιλογής του)
βότσαλα, σε οποιοδήποτε από τα εναπομείναντα κουτιά (της επιλογής του)  βότσαλα ,…, στο τέλος, στο απομένον κουτί
βότσαλα ,…, στο τέλος, στο απομένον κουτί  βότσαλα, ολοκληρώνοντας έτσι την κίνηση. Ο σκοπός του Παύλου είναι να επιτύχει μετά από κάποιο αριθμό κινήσεων κάθε κουτί να έχει ίσο αριθμό βότσαλων. Μπορεί άραγε να διαλέξει τους αριθμούς έτσι, ώστε να επιτύχει το σκοπό του σε 43 κινήσεις, αλλά να μην μπορεί σε μικρότερο μη μηδενικό αριθμό κινήσεων;
βότσαλα, ολοκληρώνοντας έτσι την κίνηση. Ο σκοπός του Παύλου είναι να επιτύχει μετά από κάποιο αριθμό κινήσεων κάθε κουτί να έχει ίσο αριθμό βότσαλων. Μπορεί άραγε να διαλέξει τους αριθμούς έτσι, ώστε να επιτύχει το σκοπό του σε 43 κινήσεις, αλλά να μην μπορεί σε μικρότερο μη μηδενικό αριθμό κινήσεων; Σημείωση: Σε κάθε κίνηση βάζουμε βότσαλα σε όλα τα 2017 κουτιά. Σε κάθε κουτί ο αριθμός των βότσαλων που που προσθέτουμε είναι ένας από το σύνολο
 . Αν ένας αριθμός
. Αν ένας αριθμός  χρησιμοποιηθεί για ένα κουτί, τότε δεν χρησιμοποιείται για άλλο κουτί της ίδιας κίνησης.
χρησιμοποιηθεί για ένα κουτί, τότε δεν χρησιμοποιείται για άλλο κουτί της ίδιας κίνησης.4. Ο δάσκαλος θέλει να δώσει στους μαθητές του πρόβλημα του ακόλουθου τύπου. Τους ανακοινώνει ότι σκέφτηκε ένα πολυώνυμο
 βαθμού 2017 με ακέραιους συντελεστές και μεγιστοβάθμιο συντελεστή ίσο με 1. Έπειτα τους ανακοινώνει
βαθμού 2017 με ακέραιους συντελεστές και μεγιστοβάθμιο συντελεστή ίσο με 1. Έπειτα τους ανακοινώνει  ακέραιους αριθμούς
ακέραιους αριθμούς  και ξεχωριστά την τιμή της παράστασης
και ξεχωριστά την τιμή της παράστασης  . Με αυτά τα δεδομένα οι μαθητές πρέπει να βρουν το πολυώνυμο, το οποίο μπορεί να σκέφτηκε ο δάσκαλος. Ποιο είναι το ελάχιστο
. Με αυτά τα δεδομένα οι μαθητές πρέπει να βρουν το πολυώνυμο, το οποίο μπορεί να σκέφτηκε ο δάσκαλος. Ποιο είναι το ελάχιστο  για το οποίο ο δάσκαλος μπορεί να θέσει πρόβλημα του παραπάνω τύπου, ώστε το πολυώνυμο, το ευρεθέν από τους μαθητές, οπωσδήποτε να ταυτίζεται με αυτό του δασκάλου;
για το οποίο ο δάσκαλος μπορεί να θέσει πρόβλημα του παραπάνω τύπου, ώστε το πολυώνυμο, το ευρεθέν από τους μαθητές, οπωσδήποτε να ταυτίζεται με αυτό του δασκάλου;Δεύτερη μέρα (31/01/2017)
5. Ο Στέλιος σχεδίασε ένα κενό πίνακα διαστάσεων
 και πάνω από κάθε στήλη και αριστερά από κάθε γραμμή έγραψε από έναν μη μηδενικό αριθμό. Προέκυψε ότι όλοι, οι 100 γραμμένοι αριθμοί, είναι διαφορετικοί μεταξύ τους και μάλιστα οι 50 από αυτούς είναι ρητοί και οι υπόλοιποι άρρητοι. Έπειτα, σε κάθε κελί του πίνακα σημείωσε το γινόμενο των αριθμών που ήταν γραμμένοι δίπλα σε κάθε γραμμή και στήλη (σχημάτισε ένα πίνακα/προπαίδεια γινομένων). Ποιος είναι ο μέγιστος αριθμός ρητών γινομένων που μπορεί να προκύψουν σε αυτό τον πίνακα;
και πάνω από κάθε στήλη και αριστερά από κάθε γραμμή έγραψε από έναν μη μηδενικό αριθμό. Προέκυψε ότι όλοι, οι 100 γραμμένοι αριθμοί, είναι διαφορετικοί μεταξύ τους και μάλιστα οι 50 από αυτούς είναι ρητοί και οι υπόλοιποι άρρητοι. Έπειτα, σε κάθε κελί του πίνακα σημείωσε το γινόμενο των αριθμών που ήταν γραμμένοι δίπλα σε κάθε γραμμή και στήλη (σχημάτισε ένα πίνακα/προπαίδεια γινομένων). Ποιος είναι ο μέγιστος αριθμός ρητών γινομένων που μπορεί να προκύψουν σε αυτό τον πίνακα;6. Στην αρχή στο πίνακα είναι γραμμένοι μερικοί (περισσότεροι του ενός) μη μηδενικοί φυσικοί αριθμοί. Στην συνέχεια κάθε λεπτό στο πίνακα γράφεται αριθμός ίσος με το άθροισμα των τετραγώνων όλων των ήδη γραμμένων αριθμών (δηλαδή αν στον πίνακα είναι γραμμένοι αριθμοί 1,2,2, τότε το πρώτο λεπτό γράφεται ο αριθμός
 ). Να αποδείξετε, ότι ο εκατοστός αριθμός που γράφεται έχει τουλάχιστον 100 διαφορετικούς πρώτους διαιρέτες.
). Να αποδείξετε, ότι ο εκατοστός αριθμός που γράφεται έχει τουλάχιστον 100 διαφορετικούς πρώτους διαιρέτες.7. Κυρτό πολύγωνο διαμερίζεται, με μη τεμνόμενες διαγώνιους, σε ισοσκελή τρίγωνα. Να αποδείξετε, ότι σε αυτό το πολύγωνο θα βρεθούν δυο ίσες πλευρές.
8. Κυκλος
 είναι περιγεγραμμένος σε τρίγωνο
είναι περιγεγραμμένος σε τρίγωνο  . Στην πλευρά
. Στην πλευρά  θεωρούμε σημείο
θεωρούμε σημείο  και στην πλευρά
και στην πλευρά  σημείο
σημείο  έτσι, ώστε
έτσι, ώστε  . Τα σημεία
. Τα σημεία  και
και  του έλασσον τόξου
του έλασσον τόξου  του
του  είναι τέτοια, ώστε
είναι τέτοια, ώστε  . Οι χορδές
. Οι χορδές  και
και 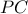 τέμνουν την ευθεία
τέμνουν την ευθεία  στα σημεία
στα σημεία  και
και  αντίστοιχα. Να αποδείξετε, ότι
αντίστοιχα. Να αποδείξετε, ότι  .
.Edit 11/02/16: Έγινε τροποποίηση στην εκφώνηση του 3ου προβλήματος της πρώτης μέρας. Η τροποποιήση είναι διευκρινιστική για το τι εννοούμε ως κίνηση.

 ικανοποιούν τις συνθήκες.
ικανοποιούν τις συνθήκες. και επειδή το
και επειδή το  είναι περιγεγραμμένο, θα είναι
είναι περιγεγραμμένο, θα είναι  , οπότε εύκολα
, οπότε εύκολα καθώς επίσης και τα
καθώς επίσης και τα  είναι ίσα), απ' όπου
είναι ίσα), απ' όπου  είναι ίσα, άρα
είναι ίσα, άρα  , οπότε τα σημεία
, οπότε τα σημεία  είναι ομοκυκλικά.
είναι ομοκυκλικά. , που προκύπτει με την παραπάνω διαδικασία θα έχει τουλάχιστον
, που προκύπτει με την παραπάνω διαδικασία θα έχει τουλάχιστον  πρώτους διαιρέτες. Έστω λοιπόν πως ισχύει ότι ο
πρώτους διαιρέτες. Έστω λοιπόν πως ισχύει ότι ο  (που προέκυψε από την
(που προέκυψε από την  έχει τουλάχιστον
έχει τουλάχιστον  διαφορετικούς πρώτους διαιρέτες. Είναι
διαφορετικούς πρώτους διαιρέτες. Είναι 
 . Ισχύει
. Ισχύει  . Συνεπώς ο
. Συνεπώς ο  , αυτός θα έχει τουλάχιστον ένα πρώτο διαιρέτη και το ζητούμενο έπεται.....
, αυτός θα έχει τουλάχιστον ένα πρώτο διαιρέτη και το ζητούμενο έπεται..... . Αν
. Αν  , ακόμη και αν ο δάσκαλος τους ανακοινώσει τις τιμές των
, ακόμη και αν ο δάσκαλος τους ανακοινώσει τις τιμές των  δεν θα μπορούν να ξεχωρίσουν μεταξύ των πολυωνύμων
δεν θα μπορούν να ξεχωρίσουν μεταξύ των πολυωνύμων 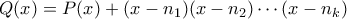
 . Ο δάσκαλος επιλέγει το πολυώνυμο
. Ο δάσκαλος επιλέγει το πολυώνυμο
 .
. . Γνωρίζουν επομένως ότι
. Γνωρίζουν επομένως ότι  ή
ή  για κάθε
για κάθε  .
.  ακέραιοι, τότε
ακέραιοι, τότε  . Οπότε για
. Οπότε για  με
με  πρέπει
πρέπει  . Άρα
. Άρα  και
και  .
. για κάθε
για κάθε  για κάθε
για κάθε  .
. με μεγιστοβάθμιο συντελεστή ίσο με
με μεγιστοβάθμιο συντελεστή ίσο με  το οποίο να ικανοποιεί
το οποίο να ικανοποιεί  .
.  είναι δύο τέτοια πολυώνυμα τότε το πολυώνυμο
είναι δύο τέτοια πολυώνυμα τότε το πολυώνυμο  είναι βαθμού
είναι βαθμού  και έχει
και έχει  , θα υπάρχουν
, θα υπάρχουν  που δεν θα έχουν. Οπότε δεν θα μπορούν ποτέ τα κουτιά εκτός ίσως από το τέλος να έχουν ίσο αριθμό από βότσαλα.
που δεν θα έχουν. Οπότε δεν θα μπορούν ποτέ τα κουτιά εκτός ίσως από το τέλος να έχουν ίσο αριθμό από βότσαλα.  . Τότε ο Πάυλος διαλέγει ένα κουτί
. Τότε ο Πάυλος διαλέγει ένα κουτί  , οποιοδήποτε, και βάζει μέσα έστω
, οποιοδήποτε, και βάζει μέσα έστω  βότσαλα , διαλέγει ένα αλλο κουτί
βότσαλα , διαλέγει ένα αλλο κουτί  και ας πούμε ότι έβαλε μέσα
και ας πούμε ότι έβαλε μέσα  βότσαλα , συνεχίζει κατά αυτό το τρόπο και στο τελευταίο κουτί
βότσαλα , συνεχίζει κατά αυτό το τρόπο και στο τελευταίο κουτί  έβαλε
έβαλε  . Έτσι ολοκληρώνει την πρώτη κίνηση.
. Έτσι ολοκληρώνει την πρώτη κίνηση.  . Στο κουτί
. Στο κουτί  βότσαλα κτλ.
βότσαλα κτλ. και
και  ) είναι ρητός.
) είναι ρητός. μέγιστο, πρέπει
μέγιστο, πρέπει  με μέγιστο πλήθος ρητών
με μέγιστο πλήθος ρητών  .
.
 είναι εγγράψιμο και άρα
είναι εγγράψιμο και άρα 

 είναι εγγράψιμο και άρα
είναι εγγράψιμο και άρα 
 ) ότι:
) ότι:

 Ο Παύλος διαλέγει
Ο Παύλος διαλέγει  αριθμούς ίσους με
αριθμούς ίσους με  ,
, 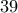 αριθμούς ίσους με
αριθμούς ίσους με  και τους υπόλοιπους αριθμούς ίσους με
και τους υπόλοιπους αριθμούς ίσους με  κινήσεις, τα κουτιά αυτά θα περιέχουν
κινήσεις, τα κουτιά αυτά θα περιέχουν  βότσαλα το καθένα. Τα υπόλοιπα κουτιά τα διαιρεί σε
βότσαλα το καθένα. Τα υπόλοιπα κουτιά τα διαιρεί σε  ο Παύλος τοποθετεί στην
ο Παύλος τοποθετεί στην  βότσαλα και ο Παύλος πέτυχε το σκοπό του.
βότσαλα και ο Παύλος πέτυχε το σκοπό του. . Σε μια κίνηση, θα πρέπει να τοποθέτησε σε κάποιο κουτί
. Σε μια κίνηση, θα πρέπει να τοποθέτησε σε κάποιο κουτί  βότσαλα. Επειδή
βότσαλα. Επειδή  θα υπάρχει κάποιο άλλο κουτί στο οποίο δεν τοποθετήθηκαν σε καμιά κίνηση
θα υπάρχει κάποιο άλλο κουτί στο οποίο δεν τοποθετήθηκαν σε καμιά κίνηση  βότσαλα. Αλλά
βότσαλα. Αλλά  οπότε τελικά τα δύο αυτά κουτιά δεν περιέχουν τον ίδιο αριθμό από βότσαλα.
οπότε τελικά τα δύο αυτά κουτιά δεν περιέχουν τον ίδιο αριθμό από βότσαλα.