Θέματα της 3ης φάσης για την 9η τάξη. Διάρκεια εξέτασης 4 ώρες/μέρα.
Πρώτη μέρα (30/01/17)
1. Σε γινόμενο τριών μη μεδενικών φυσικών αριθμών κάθε παράγοντα των μειώνουμε κατά τρία. Μπορεί άραγε, με αυτή την διαδικασία, το γινόμενο να αυξηθεί ακριβώς κατά 2016;
2. Ο Βασίλης σκέφτηκε (θεώρησε) 8 κελιά της σκακιέρας κανένα ζεύγος των οποίων δε βρίσκεται στην ίδια στήλη ή γραμμή. Με μια κίνηση, ο Πέτρος τοποθετεί στην σκακέρα 8 πύργους, που δεν απειλούν ο ένας τον άλλον. Έπειτα ο Βασίλης σημειώνει όλους τους πύργους οι οποίοι είναι τοποθετημένοι στα κελιά που είχε σκεφτεί. Αν σε αυτή την κίνηση, το πλήθος τους είναι άρτιο (δηλαδή 0,2,4,6 ή 8), τότε κερδίζει ο Πέτρος. Διαφορετικά όλοι οι πύργοι αφαιρούνται και ο Πέτρος κάνει την επόμενη κίνηση. Ποιος είναι ο ελάχιστος αριθμός κινήσεων που εξασφαλίζει την βεβαιότητα νίκης στον Πέτρο;
3. Υπάρχει άραγε τρίγωνο με μήκη πλευρών
 τέτοια, ώστε
τέτοια, ώστε  ;
;4. Ισόπλευρο τρίγωνο
 είναι εγγεγραμμένο σε κύκλο
είναι εγγεγραμμένο σε κύκλο  και περιγεγραμμένο σε κύκλο
και περιγεγραμμένο σε κύκλο  . Στις πλευρές
. Στις πλευρές  και
και  θεωρούμε τα σημεία
θεωρούμε τα σημεία  και
και  αντίστοιχα, ώστε το τμήμα
αντίστοιχα, ώστε το τμήμα  να εφάπτεται του
να εφάπτεται του  . Ο κύκλος
. Ο κύκλος  με κέντρο το
με κέντρο το  διέρχεται από το σημείο
διέρχεται από το σημείο  και ο κύκλος
και ο κύκλος  με κέντρο το
με κέντρο το  από το
από το  . Να δείξετε ότι οι κύκλοι
. Να δείξετε ότι οι κύκλοι  και
και  έχουν κοινό σημείο.
έχουν κοινό σημείο.Δεύτερη μέρα (31/01/17)
5. Ο Στέλιος σχεδίασε ένα κενό πίνακα διαστάσεων
 και πάνω από κάθε στήλη και αριστερά από κάθε γραμμή έγραψε από έναν αριθμό. Προέκυψε ότι όλοι, οι 100 γραμμένοι αριθμοί, είναι διαφορετικοί μεταξύ τους και μάλιστα οι 50 από αυτούς είναι ρητοί και οι υπόλοιποι άρρητοι. Έπειτα, σε κάθε κελί του πίνακα σημείωσε το άθροισμα των αριθμών που ήταν γραμμένοι δίπλα σε κάθε γραμμή και στήλη (σχημάτισε ένα πίνακα/προπαίδεια αθροισμάτων). Ποιος είναι ο μέγιστος αριθμός ρητών αθροισμάτων που μπορεί να προκύψουν σε αυτό τον πίνακα;
και πάνω από κάθε στήλη και αριστερά από κάθε γραμμή έγραψε από έναν αριθμό. Προέκυψε ότι όλοι, οι 100 γραμμένοι αριθμοί, είναι διαφορετικοί μεταξύ τους και μάλιστα οι 50 από αυτούς είναι ρητοί και οι υπόλοιποι άρρητοι. Έπειτα, σε κάθε κελί του πίνακα σημείωσε το άθροισμα των αριθμών που ήταν γραμμένοι δίπλα σε κάθε γραμμή και στήλη (σχημάτισε ένα πίνακα/προπαίδεια αθροισμάτων). Ποιος είναι ο μέγιστος αριθμός ρητών αθροισμάτων που μπορεί να προκύψουν σε αυτό τον πίνακα;6. Σε οξυγώνιο τίγωνο
 φέρουμε την διάμεσο
φέρουμε την διάμεσο  και το ύψος
και το ύψος  . Η κάθετος από το σημείο
. Η κάθετος από το σημείο  προς την ευθεία
προς την ευθεία  τέμνει την ευθεία
τέμνει την ευθεία  στο σημείο
στο σημείο  . Να αποδείξετε ότι αν
. Να αποδείξετε ότι αν  , τότε
, τότε  .
. 7. Κυρτό πολύγωνο διαμερίζεται, με μη τεμνομένες διαγωνίους, σε ισοσκελή τρίγωνα. Να αποδείξετε ότι σε αυτό το πολύγωνο θα βρεθούν δυο ίσες πλευρές.
8. Αρχικά σε ένα τραπέζι τοποθετήθηκαν 100 κάρτες, σε κάθε μια από τις οποίες είναι γραμμένος ένας θετικός ακέραιος. Εξάλλου ακριβώς σε 43 κάρτες είναι γραμμένοι περιττοί αριθμοί. Έπειτα, κάθε λεπτό, εφαρμόζεται η ακόλουθη διαδικασία. Για κάθε τρεις κάρτες, που βρίσκονται στο τραπέζι, υπολογίζεται το γινόμενο των αριθμών που είναι γραμμένοι σε αυτές. Όλα αυτά τα γινόμενα αθροίζονται και ο αριθμός που προκύπτει γράφεται σε μια νέα κάρτα η οποία προστίθεται στις ήδη υπάρχουσες του τραπεζιού. Ένα χρόνο μετά την έναρξη της διαδικασίας προέκυψε, ότι στο τραπέζι υπάρχει κάρτα με αριθμό που διαιρείται με το
 . Να αποδείξετε ότι αριθμός διαιρούμενος με το
. Να αποδείξετε ότι αριθμός διαιρούμενος με το  , υπήρχε σε μία από τις κάρτες ήδη μια μέρα μετά την έναρξη της διαδικασίας.
, υπήρχε σε μία από τις κάρτες ήδη μια μέρα μετά την έναρξη της διαδικασίας.
 . Αρκεί να βρούμε μια τριάδα που ικανοποιεί. Ας είναι
. Αρκεί να βρούμε μια τριάδα που ικανοποιεί. Ας είναι  . Πρέπει
. Πρέπει  . Εύκολα παίρνουμε
. Εύκολα παίρνουμε  (αφού αρκεί μόνο μια τριάδα). Συνεπώς, το ζητούμενο ισχύει για
(αφού αρκεί μόνο μια τριάδα). Συνεπώς, το ζητούμενο ισχύει για  ή αντιστοίχως
ή αντιστοίχως 


 περιττές κάρτες οπότε και
περιττές κάρτες οπότε και  περιττά γινόμενα. Επειδή ο
περιττά γινόμενα. Επειδή ο  είναι περιττός, το άθροισμα θα είναι περιττό. Έπειτα έχουμε
είναι περιττός, το άθροισμα θα είναι περιττό. Έπειτα έχουμε  περιττές κάρτες οπότε και
περιττές κάρτες οπότε και  περιττά γινόμενα. Άρα ο νέος αριθμός θα είναι άρτιος. Από εδώ και πέρα θα συνεχίζουμε να έχουμε
περιττά γινόμενα. Άρα ο νέος αριθμός θα είναι άρτιος. Από εδώ και πέρα θα συνεχίζουμε να έχουμε  ο αριθμός που γράψαμε μετά από
ο αριθμός που γράψαμε μετά από  λεπτά, ισχυρίζομαι πως για κάθε
λεπτά, ισχυρίζομαι πως για κάθε  , η μεγαλύτερη δύναμη του
, η μεγαλύτερη δύναμη του  η οποία διαιρεί τον
η οποία διαιρεί τον  , ισούται με την μεγαλύτερη δύναμη του
, ισούται με την μεγαλύτερη δύναμη του  για τους αριθμούς που είναι γραμμένοι στις
για τους αριθμούς που είναι γραμμένοι στις  κάρτες προτού υπολογίσουμε τον
κάρτες προτού υπολογίσουμε τον  όπου το
όπου το  υπολογίζεται ως εξής: Για κάθε δύο από τις κάρτες
υπολογίζεται ως εξής: Για κάθε δύο από τις κάρτες  , έστω
, έστω  . Τότε όμως είναι
. Τότε όμως είναι  και ο ισχυρισμός έπεται.
και ο ισχυρισμός έπεται. το πλήθος των Ρητών και
το πλήθος των Ρητών και  το πλήθος των Άρρητων που υπάρχουν στην οριζόντιο. Τότε πρέπει στην κατακόρυφο να είναι
το πλήθος των Άρρητων που υπάρχουν στην οριζόντιο. Τότε πρέπει στην κατακόρυφο να είναι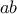 σε πλήθος ρητοί αριθμοί στον πίνακα. Στην συνέχεια θα δείξουμε πως ρητός και άρρητος δεν κάνουν ρητό.
σε πλήθος ρητοί αριθμοί στον πίνακα. Στην συνέχεια θα δείξουμε πως ρητός και άρρητος δεν κάνουν ρητό. ρητοί αριθμοί και
ρητοί αριθμοί και  ένας άρρητος αριθμός τέτοιοι ώστε:
ένας άρρητος αριθμός τέτοιοι ώστε:  Τότε θα πρέπει
Τότε θα πρέπει  όμως ο αριθμός
όμως ο αριθμός είναι ρητός ως διαφορά ρητών άρα και ο αριθμός
είναι ρητός ως διαφορά ρητών άρα και ο αριθμός  όπου
όπου  . Πράγματι, αν αθροίσουμε οποιοσδήποτε 2 αριθμούς από αυτά τα δύο σύνολα θα δώσουν ρητό άρα το μέγιστο πλήθος ρητών
. Πράγματι, αν αθροίσουμε οποιοσδήποτε 2 αριθμούς από αυτά τα δύο σύνολα θα δώσουν ρητό άρα το μέγιστο πλήθος ρητών . Όμως οι ρητοί είναι στο σύνολο
. Όμως οι ρητοί είναι στο σύνολο 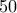 άρα
άρα . Αντικαθιστώντας στην
. Αντικαθιστώντας στην  έχουμε
έχουμε  . Επομένως ψάχνουμε την μέγιστη τιμή της παράστασης
. Επομένως ψάχνουμε την μέγιστη τιμή της παράστασης  η
η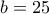 . Επομένως το μέγιστο πλήθος ρητών θα είναι
. Επομένως το μέγιστο πλήθος ρητών θα είναι  .
. ,
,  και
και  τα σημεία επαφής του
τα σημεία επαφής του  με τις
με τις  ,
,  και
και  το κέντρο και
το κέντρο και  η ακτίνα του κύκλου
η ακτίνα του κύκλου 
 και
και  είναι συνευθειακά.
είναι συνευθειακά. 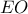 τέμνει τον κύκλο
τέμνει τον κύκλο  στο σημείο
στο σημείο  οπότε
οπότε  Άρα, τα τρίγωνα
Άρα, τα τρίγωνα  και
και  είναι ίσα (αφού
είναι ίσα (αφού  κοινή,
κοινή,  και
και  ). Επομένως, είναι
). Επομένως, είναι  δηλαδή το σημείο
δηλαδή το σημείο  Όμοια, δείχνουμε ότι το σημείο
Όμοια, δείχνουμε ότι το σημείο  και η απόδειξη ολοκληρώνεται.
και η απόδειξη ολοκληρώνεται. το τετράπλευρο
το τετράπλευρο  είναι εγγράψιμο σε κύκλο διαμέτρου
είναι εγγράψιμο σε κύκλο διαμέτρου  Άρα, από το Νόμο των Ημιτόνων στο τρίγωνο
Άρα, από το Νόμο των Ημιτόνων στο τρίγωνο  έχουμε ότι
έχουμε ότι
 η
η  είναι διάμεσος προς την υποτείνουσα, οπότε
είναι διάμεσος προς την υποτείνουσα, οπότε

 (οξείες γωνίες με πλευρές κάθετες), άρα το
(οξείες γωνίες με πλευρές κάθετες), άρα το  είναι εγγράψιμο σε
είναι εγγράψιμο σε , οπότε
, οπότε  (ως πλευρά κανονικού εξαγώνου), αλλά είναι και
(ως πλευρά κανονικού εξαγώνου), αλλά είναι και 

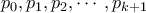 άνισες
άνισες 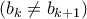 .
. 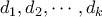 ορίζουν τα τρίγωνα
ορίζουν τα τρίγωνα 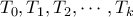 .
. είναι ισοσκελές άρα η διαγώνιος
είναι ισοσκελές άρα η διαγώνιος  θα είναι ίση με μία από τις πλευρές
θα είναι ίση με μία από τις πλευρές 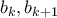 .
. στο οποίο η
στο οποίο η  ισούται με κάποια από τις διεγραμμένες πλευρές του πολυγώνου.
ισούται με κάποια από τις διεγραμμένες πλευρές του πολυγώνου.