Θέματα της πρώτης φάσης για την 9η τάξη.
1. Μπορούμε να χωρίσουμε τους φυσικούς αριθμούς από το 0 έως το 301 σε ζεύγη, τους αριθμούς κάθε ζεύγους να τους αθροίσουμε και τα αθροίσματα αυτά να τα πολλαπλασιάσουμε μεταξύ τους, ώστε το γινόμενο που προκύπτει να είναι 15η δύναμη φυσικού αριθμού;
2. Στην Μετεξεταστούπολη 6000 μαθητές συμμετείχαν στην Ενιαία Εξέταση Μετεξεταστέων, στην οποία μπορεί να πάρει κανείς από 0 έως 8 βαθμούς. Μετά την διόρθωση των γραπτών όσοι πήραν βαθμούς 1,2 και 3 τα γραπτά τους έτυχαν νέας διόρθωσης και έλαβαν τον βαθμό 0. Όσοι είχαν γράψει βαθμό 5, 6 και 7 τους έγινε διόρθωση προς τα πάνω και έλαβαν βαθμό 8 (τα υπόλοιπα αποτελέσματα δεν άλλαξαν). Μετά από αυτές τις διορθώσεις βαθμών ο μέσος όρος όλων των μαθητών αυξήθηκε κατά 0,1 βαθμούς. Να αποδείξετε ότι υπάρχουν τέτοιοι φυσικοί αριθμοί (
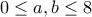 , ώστε ο αριθμός των μαθητών, που πριν τις διορθώσεις είχαν βαθμό
, ώστε ο αριθμός των μαθητών, που πριν τις διορθώσεις είχαν βαθμό  και ο αριθμός των μαθητών πριν τις διορθώσεις είχε βαθμό
και ο αριθμός των μαθητών πριν τις διορθώσεις είχε βαθμό  , διαφέρουν τουλάχιστον κατά 100.
, διαφέρουν τουλάχιστον κατά 100.3. Στη σειρά είναι γραμμένα κάμποσα μηδενικά και μονάδες. Μεταξύ οποιονδήποτε 200 διαδοχικών ψηφίων το πλήθος των μηδενικών και μονάδων είναι ίσο και μεταξύ οποιονδήποτε 202 διαδοχικών ψηφίων, διαφορετικό. Ποιος είναι ο μέγιστος αριθμός ψηφιών που μπορεί να έχει αυτή η ψηφιοσειρά;
4. Το δευτέρου βαθμού τριώνυμο
 με θετικό μεγιστοβάθμιο συντελεστή είναι τέτοιο, ώστε κάθε μία από τις ευθείες
με θετικό μεγιστοβάθμιο συντελεστή είναι τέτοιο, ώστε κάθε μία από τις ευθείες 
να τέμνει την γραφική παράστασή του το πολύ σε ένα σημείο. Ποια είναι η μέγιστη τιμή που μπορεί να πάρει η ποσότητα
 ;
;5. Στο τρίγωνο
 οι προεκτάσεις των διαμέσων από τις κορυφές
οι προεκτάσεις των διαμέσων από τις κορυφές  τέμνουν τον περιγεγραμμένο κύκλο του στα σημεία
τέμνουν τον περιγεγραμμένο κύκλο του στα σημεία  και
και  αντίστοιχα. Στις πλευρές
αντίστοιχα. Στις πλευρές  διαλέγουμε σημεία
διαλέγουμε σημεία  αντίστοιχα, ώστε
αντίστοιχα, ώστε  . Να δείξετε ότι
. Να δείξετε ότι  .
.Υγ. Η μαθηματική ολυμπιάδα της Πετρούπολης, μία από τις πιο παλιές, διεξάγεται τα τελευταία χρόνια σε δυο φάσεις. Η πρώτη φάση είναι ανοιχτή σε όλους τους μαθητές και είναι θα λέγαμε σε επίπεδο δημοτικών διαμερισμάτων. Οι νικητές της πρώτης φάσης καλούνται να διαγωνιστούν στη δεύτερη και τελική φάση (επίπεδο πόλης). Στη δεύτερη φάση διαγωνίζονται περίπου 100 μαθητές ανά τάξη και η εξέταση γίνεται στο μαθηματικό τμήμα του κρατικού πανεπιστημιίου της Πετρούπολης. Η ιδιαιτερότητα του διαγωνισμού είναι ότι η δεύτερη φάση είναι προφορική. Οι διαγωνιζόμενοι καλούνται να λύσουν αρχικά 4 προβλήματα. Όσοι καταφέρουν να λύσουν, συνήθως 2-3 προβλήματα, καλούνται να λύσουν άλλα 3 σε διαφορετική αίθουσα. Ο μαθητής έχει το δικαίωμα να πάει στην έδρα και να εξηγήσει την λύση του τρεις φορές. Κατά την διαδικασία αυτή δύναται να του ζητηθούν και περαιτέρω εξηγήσεις, γενικεύσεις κτλ. Η διόρθωση γίνεται από καθηγητές σχολείων, του πανεπιστημίου και από φοιτητές.

![[0,300] [0,300]](/forum/ext/geomar/texintegr/latexrender/pictures/3e882160598dddc2f643834b947b4d5a.png) είναι
είναι  σε αριθμό...
σε αριθμό...  το βαρύκεντρο του τριγώνου. Επειδή
το βαρύκεντρο του τριγώνου. Επειδή 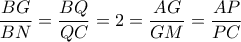 , το
, το  είναι παραλληλόγραμμο
είναι παραλληλόγραμμο  είναι εγγράψιμα. Άρα:
είναι εγγράψιμα. Άρα: 
 (έχουμε ένα ζεύγος της μορφής
(έχουμε ένα ζεύγος της μορφής  ,
,  και
και  της μορφής
της μορφής  . Επομένως, το γινόμενο είναι ίσο με
. Επομένως, το γινόμενο είναι ίσο με  .
. .
. ας γράψουμε
ας γράψουμε  για το πλήθος των μαθητών που έλαβαν βαθμό
για το πλήθος των μαθητών που έλαβαν βαθμό  . Μετά τις διορθώσεις, το άθροισμα των βαθμών των μαθητών αυξήθηκε κατά
. Μετά τις διορθώσεις, το άθροισμα των βαθμών των μαθητών αυξήθηκε κατά 
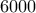 μαθητές και ο μέσος όρος αυξήθηκε κατά
μαθητές και ο μέσος όρος αυξήθηκε κατά 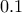 , αυτό σημαίνει ότι
, αυτό σημαίνει ότι  .
. ή
ή  ή
ή  αφού σε αντίθετη περίπτωση θα είχαμε
αφού σε αντίθετη περίπτωση θα είχαμε  .
.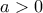 , η διακρίνουσα
, η διακρίνουσα  για κάθε μία από τις παρακάτω εξισώσεις θα πρέπει να είναι μικρότερη ή ίση του μηδενός.
για κάθε μία από τις παρακάτω εξισώσεις θα πρέπει να είναι μικρότερη ή ίση του μηδενός.  (1)
(1) (2)
(2) (3)
(3)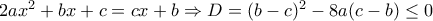 (4)
(4) (5)
(5) (6)
(6) (7)
(7) οπότε και οι (4) και (6) γίνονται
οπότε και οι (4) και (6) γίνονται 

 ισχύουν τα δεδομένα του προβλήματος...
ισχύουν τα δεδομένα του προβλήματος...