Θέματα της 2ης φάσης για την 11η τάξη. Διάρκεια εξέτασης υπολογισμένη για 240 λεπτά.
1. Έχει η εξίσωση

αρνητικές ρίζες;
2. Ο Βασίλης έγραψε στα κελιά πίνακα
 τους αριθμούς από το 1 έως το 72 με κάποια σειρά γνωστή μόνο σε αυτόν. Έπειτα για κάθε μία από τις δεκαοχτώ στήλες πολλαπλασίασε τους τέσσερεις αριθμούς της στήλης μεταξύ τους και υπολόγισε το άθροισμα των ψηφιών του γινομένου. Μπορούν και τα δεκαοχτώ αθροίσματα να είναι ίσα;
τους αριθμούς από το 1 έως το 72 με κάποια σειρά γνωστή μόνο σε αυτόν. Έπειτα για κάθε μία από τις δεκαοχτώ στήλες πολλαπλασίασε τους τέσσερεις αριθμούς της στήλης μεταξύ τους και υπολόγισε το άθροισμα των ψηφιών του γινομένου. Μπορούν και τα δεκαοχτώ αθροίσματα να είναι ίσα;3. Κανονικό πεντάγωνο και κανονικό εικοσάγωνο είναι εγγεγραμμένα στον ίδιο κύκλο. Πιο είναι μεγαλύτερο το άθροισμα των τετραγώνων όλων των πλευρών του πενταγώνου ή το άθροισμα των τετραγώνων όλων των πλευρών του εικοσάγωνου;
4. Δίνεται η τριγωνική πυραμίδα
 με ορθές επίπεδες γωνίες στην κορυφή
με ορθές επίπεδες γωνίες στην κορυφή  ,στην οποία
,στην οποία  . Να δείξετε ότι το άθροισμα των επίπεδων γωνιών στην κορυφή
. Να δείξετε ότι το άθροισμα των επίπεδων γωνιών στην κορυφή  είναι
είναι  .
.5. Η συνάρτηση
 ορισμένη στο σύνολο όλων των πραγματικών αριθμών και ικανοποιεί τις σχέσεις:
ορισμένη στο σύνολο όλων των πραγματικών αριθμών και ικανοποιεί τις σχέσεις: και
και  για κάθε
για κάθε  .
.Να δείξετε ότι η
 είναι περιοδική συνάρτηση.
είναι περιοδική συνάρτηση.6. Κάθε ακέραιος αριθμός στον άξονα των αριθμών χρωματίζεται με ένα από δυο χρώματα, άσπρο ή μαύρο. Εξάλλου οι αριθμοί 2016 και 2017 χρωματίστηκαν με διαφορετικό χρώμα. Θα βρεθούν οπωσδήποτε τρεις ακέραιοι αριθμοί ίδιου χρώματος, το άθροισμα των οποίων ισούται με μηδέν;

 , άτοπο.
, άτοπο. έχει άθροισμα ψηφίων πολ. του
έχει άθροισμα ψηφίων πολ. του  -
-  είναι
είναι  σε πλήθος. Ενώ, τα πολλαπλάσια του
σε πλήθος. Ενώ, τα πολλαπλάσια του  είναι
είναι  . Όμως, σε αυτά εντάσσονται και τα πολ του
. Όμως, σε αυτά εντάσσονται και τα πολ του  σε αριθμό. Είναι προφανές ότι για να διαιρείται το γινόμενο των τεσσάρων αριθμών μιας στήλης με το
σε αριθμό. Είναι προφανές ότι για να διαιρείται το γινόμενο των τεσσάρων αριθμών μιας στήλης με το  ζεύγη του
ζεύγη του  πολλαπλάσια του
πολλαπλάσια του  . Συνεπώς θα υπάρχουν τουλάχιστον
. Συνεπώς θα υπάρχουν τουλάχιστον  γινόμενα που δεν θα διαιρούνται με το
γινόμενα που δεν θα διαιρούνται με το  η ακτίνα του κύκλου,
η ακτίνα του κύκλου,  το άθροισμα των τετραγώνων όλων των πλευρών του πενταγώνου και
το άθροισμα των τετραγώνων όλων των πλευρών του πενταγώνου και  το άθροισμα των τετραγώνων όλων των πλευρών του εικοσάγωνου. Θα δείξω ότι
το άθροισμα των τετραγώνων όλων των πλευρών του εικοσάγωνου. Θα δείξω ότι 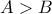

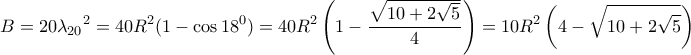
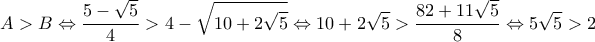
 διότι
διότι
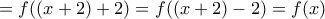 .
. γιατί
γιατί  κλπ
κλπ .
. είναι η ελάχιστη θετική περίοδος (αν υπάρχει)τότε το μόνο που μπορούμε να πούμε είναι ότι
είναι η ελάχιστη θετική περίοδος (αν υπάρχει)τότε το μόνο που μπορούμε να πούμε είναι ότι


 θα έχει το ίδιο χρώμα ή με το
θα έχει το ίδιο χρώμα ή με το  ή με το
ή με το  . Έχουμε λοιπόν δύο περιπτώσεις:
. Έχουμε λοιπόν δύο περιπτώσεις: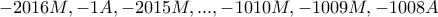 . Θα πρέπει ακόμα:
. Θα πρέπει ακόμα:  .
.  όμως δεν μπορεί να είναι Άσπρο, γιατί οι αριθμοί
όμως δεν μπορεί να είναι Άσπρο, γιατί οι αριθμοί  είναι Άσπροι με άθροισμα
είναι Άσπροι με άθροισμα  είναι Μαύροι με άθροισμα
είναι Μαύροι με άθροισμα  και συνεχίζοντας, πρέπει
και συνεχίζοντας, πρέπει  .
. δεν μπορεί να είναι Άσπρο, γιατί οι αριθμοί
δεν μπορεί να είναι Άσπρο, γιατί οι αριθμοί  είναι Άσπροι με άθροισμα
είναι Άσπροι με άθροισμα  είναι Μαύροι με άθροισμα
είναι Μαύροι με άθροισμα  -γωνο (δεδομένης ακτίνας) ορίζουμε
-γωνο (δεδομένης ακτίνας) ορίζουμε  ως το άθροισμα των τετραγώνων όλων των πλευρών του πολυγώνου. Δείξτε ότι
ως το άθροισμα των τετραγώνων όλων των πλευρών του πολυγώνου. Δείξτε ότι  . [Άρα
. [Άρα 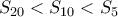 .]
.] για
για  αλλά δεν έχω σύντομη λύση για αυτό.]
αλλά δεν έχω σύντομη λύση για αυτό.] -γώνου.
-γώνου. που ισχύει όταν η γωνία
που ισχύει όταν η γωνία 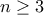 , αυτό θα ισχύει σε κάθε
, αυτό θα ισχύει σε κάθε