Πολύ ωραία η απόδειξη του Δημήτρη.
Έχω κάποιες ερωτήσεις/ιδέες σχετικά με περεταίρω προβλήματα:
1) Έγραψα κώδικα ο οποίος για κάθε πρώτο αριθμό μου επιστρέφει την θέση που εμφανίζεται ο πρώτος αυτός στην ακολουθία. Πχ ο αριθμός 2 εμφανίζεται στην θέση 2 κοκ. Επιπλέον για κάθε τέτοιο πρώτο αριθμό ο κώδικας επιστρέφει τον λόγο (ratio) της θέσης στην οποία εμφανίζεται ο αριθμός ως προς τον αριθμό.(δηλαδή για τον p=2 ο λόγος θα είναι 2/2=1 κοκ). Επιστρέφω κάποια ποτελέσματα κάτωθι:
p= 103 location is 221 ratio is 2.14563106796
p= 107 location is 232 ratio is 2.16822429907
p= 109 location is 237 ratio is 2.17431192661
p= 113 location is 246 ratio is 2.17699115044
p= 127 location is 273 ratio is 2.14960629921
p= 131 location is 282 ratio is 2.15267175573
p= 137 location is 295 ratio is 2.15328467153
p= 139 location is 300 ratio is 2.15827338129
p= 149 location is 323 ratio is 2.1677852349
p= 151 location is 328 ratio is 2.17218543046
p= 157 location is 337 ratio is 2.14649681529
p= 163 location is 354 ratio is 2.1717791411
p= 167 location is 363 ratio is 2.17365269461
p= 173 location is 374 ratio is 2.16184971098
p= 179 location is 385 ratio is 2.15083798883
p= 181 location is 392 ratio is 2.16574585635
p= 191 location is 413 ratio is 2.16230366492
p= 193 location is 422 ratio is 2.18652849741
p= 197 location is 429 ratio is 2.17766497462
p= 199 location is 434 ratio is 2.18090452261
p= 211 location is 451 ratio is 2.13744075829
p= 223 location is 478 ratio is 2.14349775785
p= 227 location is 489 ratio is 2.15418502203
p= 229 location is 496 ratio is 2.16593886463
p= 233 location is 505 ratio is 2.16738197425
p= 239 location is 522 ratio is 2.18410041841
p= 241 location is 527 ratio is 2.1867219917
p= 251 location is 540 ratio is 2.15139442231
p= 257 location is 549 ratio is 2.13618677043
p= 263 location is 570 ratio is 2.16730038023
p= 269 location is 581 ratio is 2.15985130112
p= 271 location is 588 ratio is 2.16974169742
p= 277 location is 601 ratio is 2.16967509025
p= 281 location is 610 ratio is 2.17081850534
p= 283 location is 619 ratio is 2.18727915194
p= 293 location is 636 ratio is 2.17064846416
p= 307 location is 667 ratio is 2.17263843648
p= 311 location is 674 ratio is 2.16720257235
p= 313 location is 681 ratio is 2.17571884984
p= 317 location is 690 ratio is 2.17665615142
p= 331 location is 719 ratio is 2.17220543807
p= 337 location is 728 ratio is 2.16023738872
p= 347 location is 753 ratio is 2.17002881844
p= 349 location is 758 ratio is 2.17191977077
p= 353 location is 765 ratio is 2.1671388102
p= 359 location is 778 ratio is 2.16713091922
p= 367 location is 793 ratio is 2.16076294278
p= 373 location is 808 ratio is 2.16621983914
p= 379 location is 819 ratio is 2.16094986807
p= 383 location is 830 ratio is 2.16710182768
p= 389 location is 847 ratio is 2.17737789203
p= 397 location is 860 ratio is 2.16624685139
p= 401 location is 867 ratio is 2.16209476309
p= 409 location is 884 ratio is 2.16136919315
p= 419 location is 903 ratio is 2.15513126492
p= 421 location is 908 ratio is 2.1567695962
...
...
...
p= 643 location is 1391 ratio is 2.1632970451
p= 647 location is 1400 ratio is 2.16383307573
p= 653 location is 1413 ratio is 2.16385911179
p= 659 location is 1428 ratio is 2.16691957511
p= 661 location is 1433 ratio is 2.16792738275
p= 673 location is 1458 ratio is 2.16641901932
p= 677 location is 1467 ratio is 2.16691285081
p= 683 location is 1478 ratio is 2.16398243045
p= 691 location is 1499 ratio is 2.16931982634
p= 701 location is 1520 ratio is 2.16833095578
p= 709 location is 1533 ratio is 2.16220028209
p= 719 location is 1552 ratio is 2.15855354659
p= 727 location is 1573 ratio is 2.16368638239
p= 733 location is 1582 ratio is 2.15825375171
p= 739 location is 1601 ratio is 2.16644113667
p= 743 location is 1608 ratio is 2.16419919246
Παρατηρώ οτι ο λόγος της θέσης που εμφανίζεται ενας πρώτος ως προς τον πρώτο είναι πάντα κάπου ανάμεσα στο 2.13 και 2.19. Αυτή η παρατήρηση ισχύει και για αρκετά μεγαλύτερους πρώτους. Αναρωτιέμαι αν μπορούμε να αποδείξουμε οτι ο λόγος τείνει σε κάποιο όριο (πχ 2.16) ή εαν τουλάχιστον ο λόγος είναι άνω και κάτω φραγμένος.
2) Αρχικά διαβάζοντας το πρόβλημα, το διάβασα λάθος και θεώρησα οτι κάθε αριθμός

που εμφανίζεται είναι ο μικρότερος που είναι σχετικά πρώτος με τον
 και
και με τον

. Γράφοντας κώδικα φαίνεται οτι ισχύει οτι και σε αυτή την περίπτωση όλοι οι θετικοί ακέραιοι εμφανίζονται. Θεωρώ είναι ενδιαφέρον να δείξουμε εαν ισχύει ή όχι.
 δευτέρου βαθμού με ακέραιους συντελεστές τέτοιο, ώστε
δευτέρου βαθμού με ακέραιους συντελεστές τέτοιο, ώστε  ;
; (
( ) και σημείο
) και σημείο  στον περιγεγραμμένο κύκλο του τέτοιο ώστε
στον περιγεγραμμένο κύκλο του τέτοιο ώστε  . Να αποδείξετε ότι
. Να αποδείξετε ότι  .
. χρωματίζονται με τέσσερα χρώματα. Θεωρούμε όλους τους τρόπους τοποθέτησης εσωτερικά αυτού του τετραγώνου σχήματος ταυ (
χρωματίζονται με τέσσερα χρώματα. Θεωρούμε όλους τους τρόπους τοποθέτησης εσωτερικά αυτού του τετραγώνου σχήματος ταυ ( ) των τεσσάρων κελιών (μπορεί και περιστροφές του). Να αποδείξετε ότι το σχήμα περιέχει τέσσερα διαφορετικά χρώματα λιγότερο από το 51% αυτών των περιπτώσεων.
) των τεσσάρων κελιών (μπορεί και περιστροφές του). Να αποδείξετε ότι το σχήμα περιέχει τέσσερα διαφορετικά χρώματα λιγότερο από το 51% αυτών των περιπτώσεων.  ικανοποιούν την συνθήκη
ικανοποιούν την συνθήκη
 .
. . Ο περιγεγραμμένος κύκλος του τριγώνου
. Ο περιγεγραμμένος κύκλος του τριγώνου  τέμνει τις πλευρές
τέμνει τις πλευρές  και
και  στα σημεία
στα σημεία  και
και  αντίστοιχα. Ο περιγεγραμμένος κύκλος του τριγώνου
αντίστοιχα. Ο περιγεγραμμένος κύκλος του τριγώνου  τέμνει τις πλευρές
τέμνει τις πλευρές  και
και  στα σημεία
στα σημεία  και
και  αντίστοιχα. Αν το τετράπλευρο
αντίστοιχα. Αν το τετράπλευρο  είναι παραλληλόγραμμο να αποδείξετε ότι και το
είναι παραλληλόγραμμο να αποδείξετε ότι και το  θα είναι παραλληλόγραμμο.
θα είναι παραλληλόγραμμο.  πλανήτες, οποιοιδήποτε δύο από τους οποίους συνδέονται με μια κοσμική γραμμή διπλής κατεύθυνσης. Αυτές οι συνδέσεις εξυπηρετούνται από 2015 μεταφορικές εταιρείες. Ο αυτοκράτορας θέλει να κλείσει
πλανήτες, οποιοιδήποτε δύο από τους οποίους συνδέονται με μια κοσμική γραμμή διπλής κατεύθυνσης. Αυτές οι συνδέσεις εξυπηρετούνται από 2015 μεταφορικές εταιρείες. Ο αυτοκράτορας θέλει να κλείσει  από αυτές τις εταιρίες έτσι, ώστε, χρησιμοποιώντας τις υπόλοιπες να μπορεί κάποιος να βρει τρόπο να μεταφερθεί από οποιοδήποτε πλανήτη σε κάποιον άλλο. Για ποιο μέγιστο
από αυτές τις εταιρίες έτσι, ώστε, χρησιμοποιώντας τις υπόλοιπες να μπορεί κάποιος να βρει τρόπο να μεταφερθεί από οποιοδήποτε πλανήτη σε κάποιον άλλο. Για ποιο μέγιστο  με σιγουριά μπορεί να επιτευχθεί ένα τέτοιο πλάνο;
με σιγουριά μπορεί να επιτευχθεί ένα τέτοιο πλάνο; - ο ελάχιστος φυσκός αριθμός, που δεν έχει εμφανιστεί πιο πριν (στην ακολουθία),σχετικά πρώτος με τον
- ο ελάχιστος φυσκός αριθμός, που δεν έχει εμφανιστεί πιο πριν (στην ακολουθία),σχετικά πρώτος με τον  και σχετικά μη πρώτος με τον
και σχετικά μη πρώτος με τον  . Να αποδείξετε, ότι σε αυτή την ακολουθία εμφανίζονται ακριβώς από μια φορά όλοι οι φυσικοί αριθμοί.
. Να αποδείξετε, ότι σε αυτή την ακολουθία εμφανίζονται ακριβώς από μια φορά όλοι οι φυσικοί αριθμοί.


 .Το
.Το  είναι ισοσκελές τραπέζιο:
είναι ισοσκελές τραπέζιο: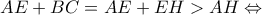

 ώστε
ώστε οπότε η αποδεικτέα γράφεται
οπότε η αποδεικτέα γράφεται



 ικανοποιεί το ζητούμενο. Τότε το
ικανοποιεί το ζητούμενο. Τότε το  είναι ρίζα του
είναι ρίζα του 
 και
και  .
. οπότε
οπότε  . Αντικαθιστώντας στην πρώτη παίρνω
. Αντικαθιστώντας στην πρώτη παίρνω

 , για να έχει ακέραια ρίζα, πρέπει η διακρίνουσά του να είναι τέλειο τετράγωνο. Όμως
, για να έχει ακέραια ρίζα, πρέπει η διακρίνουσά του να είναι τέλειο τετράγωνο. Όμως
 στους ακεραίους είναι οι
στους ακεραίους είναι οι  . (Εύκολο αφού
. (Εύκολο αφού  .) Πρέπει λοιπόν
.) Πρέπει λοιπόν  που δίνει
που δίνει  , άτοπο.
, άτοπο.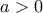 και
και 

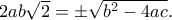
 , ο αριθμός
, ο αριθμός  είναι επίσης ρίζα του
είναι επίσης ρίζα του 
 απ' όπου έπεται ότι
απ' όπου έπεται ότι  και
και  .
.  , έπεται ότι
, έπεται ότι  ,
,  και
και 
 η οποία δεν έχει ακέραια ρίζα, άτοπο.
η οποία δεν έχει ακέραια ρίζα, άτοπο. , τότε
, τότε  , απ' όπου έπεται ότι
, απ' όπου έπεται ότι 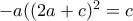 .
. η οποία δίνει
η οποία δίνει  ή
ή  , κι άρα
, κι άρα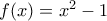 ή
ή 

 των ταυ του
των ταυ του  όλων των ταυ, θα μπορούν να είναι παρδαλά. Αν προσθέσουμε και όλα τα υπόλοιπα (που είναι το
όλων των ταυ, θα μπορούν να είναι παρδαλά. Αν προσθέσουμε και όλα τα υπόλοιπα (που είναι το  ) θα έχουμε το πολύ
) θα έχουμε το πολύ  .
. τετράγωνο αλλά τελικά δεν δουλεύει αφού ο πιο κάτω χρωματισμός έχει 5 στα 8 ταυ παρδαλά.
τετράγωνο αλλά τελικά δεν δουλεύει αφού ο πιο κάτω χρωματισμός έχει 5 στα 8 ταυ παρδαλά.
![\begin{tikzpicture}[line cap=round,line join=round,>=triangle 45,x=1.0cm,y=1.0cm]
\clip(1.5,0.68) rectangle (5.44,4.36);
\draw (2.,3.)-- (2.,2.);
\draw (2.,2.)-- (5.,2.);
\draw (5.,2.)-- (5.,3.);
\draw (5.,3.)-- (2.,3.);
\draw (3.,4.)-- (3.,1.);
\draw (3.,1.)-- (4.,1.);
\draw (4.,1.)-- (4.,4.);
\draw (4.,4.)-- (3.,4.);
\end{tikzpicture} \begin{tikzpicture}[line cap=round,line join=round,>=triangle 45,x=1.0cm,y=1.0cm]
\clip(1.5,0.68) rectangle (5.44,4.36);
\draw (2.,3.)-- (2.,2.);
\draw (2.,2.)-- (5.,2.);
\draw (5.,2.)-- (5.,3.);
\draw (5.,3.)-- (2.,3.);
\draw (3.,4.)-- (3.,1.);
\draw (3.,1.)-- (4.,1.);
\draw (4.,1.)-- (4.,4.);
\draw (4.,4.)-- (3.,4.);
\end{tikzpicture}](/forum/ext/geomar/texintegr/latexrender/pictures/0b5a7543131705d34e24b3120bece1fd.png)
 ταυ ο καθένας και κάθε χρωματισμός τους έχει το πολύ δύο παρδαλά ταυ. Πράγματι, αφού ο Σταυρός έχει
ταυ ο καθένας και κάθε χρωματισμός τους έχει το πολύ δύο παρδαλά ταυ. Πράγματι, αφού ο Σταυρός έχει  τετράγωνα σε κάθε χρωματισμό θα έχουμε τουλάχιστον δύο τετράγωνα με το ίδιο χρώμα. Οποιαδήποτε δύο τετράγωνα όμως ανήκουν σε τουλάχιστον δύο ταυ. (Απλός έλεγχος τριών διαφορετικών περιπτώσεων.)
τετράγωνα σε κάθε χρωματισμό θα έχουμε τουλάχιστον δύο τετράγωνα με το ίδιο χρώμα. Οποιαδήποτε δύο τετράγωνα όμως ανήκουν σε τουλάχιστον δύο ταυ. (Απλός έλεγχος τριών διαφορετικών περιπτώσεων.) τετράγωνο περιέχει
τετράγωνο περιέχει  τέτοιους σταυρούς. (Το κέντρο του σταυρού πρέπει να βρίσκεται στο εσωτερικό
τέτοιους σταυρούς. (Το κέντρο του σταυρού πρέπει να βρίσκεται στο εσωτερικό  τετράγωνο.) Κάθε σταυρός έχει ακριβώς τέσσερα ταυ εκ των οποίων το πολύ τα δύο είναι παρδαλά. Επίσης κάθε παρδαλό ταυ ανήκει σε ακριβώς έναν σταυρό εκτός από αυτά που έχουν το κέντρο τους στον περίγυρο του μεγάλου τετραγώνου.
τετράγωνο.) Κάθε σταυρός έχει ακριβώς τέσσερα ταυ εκ των οποίων το πολύ τα δύο είναι παρδαλά. Επίσης κάθε παρδαλό ταυ ανήκει σε ακριβώς έναν σταυρό εκτός από αυτά που έχουν το κέντρο τους στον περίγυρο του μεγάλου τετραγώνου.  ταυ. Ο δεύτερος προσθετέος προέρχεται από το ότι έχουμε
ταυ. Ο δεύτερος προσθετέος προέρχεται από το ότι έχουμε  ταυ που εφάπτονται σε κάθε μία πλευρά.
ταυ που εφάπτονται σε κάθε μία πλευρά.  είναι παρδαλά.
είναι παρδαλά.
 εταιρίες αλλά όχι περισσότερες.
εταιρίες αλλά όχι περισσότερες.  και
και  με
με  εταιρίες αντίστοιχα. Αρκεί να δείξουμε πως για τουλάχιστον ένα από τα δύο σύνολα εταιριών μπορούμε να μεταφερθούμε από οποιοδήποτε πλανήτη σε οποιοδήποτε άλλο χρησιμοποιώντας μόνο εταιρίες από αυτό το σύνολο.
εταιρίες αντίστοιχα. Αρκεί να δείξουμε πως για τουλάχιστον ένα από τα δύο σύνολα εταιριών μπορούμε να μεταφερθούμε από οποιοδήποτε πλανήτη σε οποιοδήποτε άλλο χρησιμοποιώντας μόνο εταιρίες από αυτό το σύνολο. ώστε να μην μπορούμε να μετακινηθούμε από την πόλη
ώστε να μην μπορούμε να μετακινηθούμε από την πόλη  στην πόλη
στην πόλη  χρησιμοποιώντας μόνο εταιρίες του συνόλου
χρησιμοποιώντας μόνο εταιρίες του συνόλου  , είτε οι
, είτε οι  συνδέονται με μια εταιρεία του
συνδέονται με μια εταιρεία του  συνδέονται με μια εταιρεία του
συνδέονται με μια εταιρεία του  τουλάχιστον ένα από τα
τουλάχιστον ένα από τα  είναι συνεκτικό.)
είναι συνεκτικό.) πόλεις, μια για κάθε υποσύνολο του
πόλεις, μια για κάθε υποσύνολο του  μεγέθους
μεγέθους  όπου το
όπου το  πόλεις. Αν έχουμε αντιπαράδειγμα με
πόλεις. Αν έχουμε αντιπαράδειγμα με  πόλεις μπορούμε να κατασκευάσουμε αντιπαράδειγμα με
πόλεις μπορούμε να κατασκευάσουμε αντιπαράδειγμα με  πόλεις ως εξής: Παίρνουμε αυθαίρετα μια πόλη
πόλεις ως εξής: Παίρνουμε αυθαίρετα μια πόλη  συνδέοντας την
συνδέοντας την  . Επίσης για κάθε άλλη πόλη
. Επίσης για κάθε άλλη πόλη  και μετά διαχωρίζει ρητά και άρρητα μέλη της εξίσωσης.
και μετά διαχωρίζει ρητά και άρρητα μέλη της εξίσωσης. με
με  υπάρχουν άπειροι αριθμοί
υπάρχουν άπειροι αριθμοί  με
με  και
και  .
.  . Έστω
. Έστω  η πρώτη φορά που εμφανίζεται ένα πολλαπλάσιο του
η πρώτη φορά που εμφανίζεται ένα πολλαπλάσιο του  . Αν δεν εμφανίζεται κανένα πολλαπλάσιο του
. Αν δεν εμφανίζεται κανένα πολλαπλάσιο του  .
.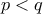 πρώτοι με
πρώτοι με  τότε είναι και
τότε είναι και  και επιπλέον
και επιπλέον  .
. . Αυτό σημαίνει ότι
. Αυτό σημαίνει ότι  και
και  . Επειδή όμως
. Επειδή όμως  τότε είτε ήδη έχει εμφανιστεί ο
τότε είτε ήδη έχει εμφανιστεί ο  στην ακολουθία (πριν τον
στην ακολουθία (πριν τον  ) είτε
) είτε  . Και στις δύο περιπτώσεις παίρνουμε
. Και στις δύο περιπτώσεις παίρνουμε  .
. όλοι οι πρώτοι οι οποίοι είναι μικρότεροι του
όλοι οι πρώτοι οι οποίοι είναι μικρότεροι του  . Σε κάποια φάση η ακολουθία θα έχει όρο
. Σε κάποια φάση η ακολουθία θα έχει όρο  με
με  . Έστω
. Έστω  . Τότε στην θέση του
. Τότε στην θέση του  ο οποίος είναι μικρότερος, άτοπο. [Αφού
ο οποίος είναι μικρότερος, άτοπο. [Αφού  και
και  .]
.] . Έστω
. Έστω  ώστε
ώστε  . Παίρνουμε ένα πρώτο
. Παίρνουμε ένα πρώτο  με
με  και
και  . Τέτοιος
. Τέτοιος  ο οποίος δεν έχει εμφανιστεί, άτοπο.
ο οποίος δεν έχει εμφανιστεί, άτοπο. με
με  πολλαπλάσιο του
πολλαπλάσιο του  για κάθε
για κάθε  . Παίρνω
. Παίρνω  . Τότε στην θέση
. Τότε στην θέση  μπορώ να γράψω τον
μπορώ να γράψω τον  ο μικρότερος αριθμός ο οποίος δεν εμφανίζεται στην ακολουθία. Έστω
ο μικρότερος αριθμός ο οποίος δεν εμφανίζεται στην ακολουθία. Έστω  ώστε
ώστε  για κάθε
για κάθε  . Παίρνουμε
. Παίρνουμε  ώστε
ώστε  για κάποιο
για κάποιο  . Τότε μπορώ να γράψω
. Τότε μπορώ να γράψω  εκτός και αν
εκτός και αν  για κάποιο
για κάποιο  . Αλλά τότε μπορώ να γράψω
. Αλλά τότε μπορώ να γράψω  εκτός και αν
εκτός και αν  για κάποιο
για κάποιο  κ.ο.κ.
κ.ο.κ. έχει
έχει  . Αυτό όμως είναι άτοπο από το Λήμμα 4 αφού θα υπάρχει πρώτος
. Αυτό όμως είναι άτοπο από το Λήμμα 4 αφού θα υπάρχει πρώτος  και
και  . Άρα και η απόδειξη του Λήμματος 5 ολοκληρώθηκε.
. Άρα και η απόδειξη του Λήμματος 5 ολοκληρώθηκε.